Свойство основной задачи линейного программирования

Лекция 12. Основная задача линейного программирования

Во многих областях деятельности возникают задачи оптимизации решений, для которых характерны следующие черты: • показатель эффективности W представляет линейную функцию от элементов решения x 1 , x 2 , …; • ограничения, налагаемые на возможные решения, имеют вид линейных равенств или неравенств. Такие задачи принято называть задачами линейного программирования .

12.1. Математическая модель основной задачи линейного программирования

Основной задачей линейного программирования (ОЗЛП) называется задача линейного программирования с ограничениями – равенствами. От задачи с ограничениями – неравенствами можно перейти к ОЗЛП и обратно. Основная задача линейного программирования формулируется следующим образом [5, 21,28]. Имеется ряд переменных x 1 , x 2 ,…, x n . Требуется найти такие неотрицательные значения этих переменных, которые удовлетворяли бы системе линейных уравнений:

a 11 x 1 + a 12 x 2 + . + a 1 n x n = b 1 ; a 21 x 1 + a 22 x 2 + . + a 2 n x n = b 2 ; . a m 1 x 1 + a m 2 x 2 + . + a mn x n = b m ,

и обращали бы в минимум линейную целевую функцию
L = c 1 x 1 + c 2 x 2 +…+ c п x n .	(12.2)

Если линейную функцию L нужно обратить в максимум, то вместо нее надо рассмотреть функцию L ´ = – L . Допустимым решением ОЗЛП называется любая совокупность переменных x 1 ≥ 0, x 2 ≥ 0,…, x n ≥ 0, удовлетворяющую уравнениям (12.1). Оптимальным решением будем называть то из допустимых решений, при котором линейная функция (12.2) обращается в минимум. ОЗЛП необязательно должна иметь решение. Может оказаться, что: 1) уравнения (12.1) противоречат друг другу; 2) уравнения (12.1) имеют решение, но не в области неотрицательных значений x 1 , x 2 ,…, x n (ОЗЛП не имеет допустимых решений); 3) допустимые решения ОЗЛП существуют, но среди них нет оптимального (функция L в области допустимых решений не ограничена снизу). Существование допустимых решений ОЗЛП. Прежде чем перейти к формулировке условий существования, приведем некоторые необходимые определения из линейной алгебры. Матрицей системы линейных уравнений (12.1) называется таблица, составленная из коэффициентов при x 1 , x 2 ,…, x n . Расширенной матрицей линейных уравнений называется та же таблица, дополненная столбцом свободных членов b i . Рангом матрицы называется наибольший порядок отличного от нуля определителя, который можно получить, вычеркивая из матрицы какие-то строки и какие-то столбцы. Для совместности системы линейных уравнений (12.1) необходимо и достаточно, чтобы ранг матрицы системы был равен рангу ее расширенной матрицы . Этот общий ранг r называется рангом системы ; он представляет число линейно независимых уравнений среди 63

наложенных ограничений. Ранг системы r не может быть больше числа уравнений т : r ≤ т и не может быть больше общего числа переменных п : r ≤ п . Случай, когда r = п . Система уравнений – ограничений ОЗЛП имеет единственное решение x 1 , x 2 ,…, x n . Если в этом решении хотя бы одна из величин x 1 , x 2 ,…, x n отрицательна, это значит, что полученное решение недопустимо и, следовательно, ОЗЛП не имеет решения. Если все решения x 1 , x 2 ,…, x n неотрицательны, то найденное решение является допустимым . Оно же является и оптимальным . Случай, когда r < п . Тогда, если система совместна, у нее существует бесчисленное множество решений. При этом п – r переменным мы можем придавать произвольные значения (так называемые свободные переменные ), а остальные r выразятся через них (эти r переменных называются базисными ). Если среди решений нет ни одного, для которого все x 1 , x 2 ,…, x n неотрицательны, то это значит, что ОЗЛП не имеет допустимого решения . Если же существуют решения системы (12.1), для которых все x 1 , x 2 ,…, x n неотрицательны, то каждое из них допустимо. Теперь необходимо найти среди допустимых решений оптимальное , т.е. такое решение x 1 , x 2 ,…, x n , для которого линейная функция L (12.2) обращается в минимум. Геометрически область допустимых решений (если она существует) представляет собой выпуклый k -мерный многогранник ( k = п – т ), т.е. часть пространства, для которой выполнены все условия: x 1 ≥ 0, x 2 ≥ 0,…, x n ≥ 0. Решение, лежащее в одной из вершин области допустимых решений, называется опорным решением , а сама вершина – опорной точкой . Решение основной задачи линейного программирования обладает следующими свойствами при любых значениях числа переменных п и числа уравнений т < п : 1. Оптимальное решение, если оно существует, лежит не внутри, а на границе области допустимых решений, в одной из опорных точек , в каждой из которых по крайней мере k из переменных обращаются в нуль. 2. Для того, чтобы найти оптимальное решение, нужно, переходя от одной опорной точки к другой, двигаться в направлении уменьшения линейной функции L , которую требуется минимизировать.

12.2. Задача линейного программирования с ограничениями-неравенствами

Довольно часто ограничения в задаче линейного программирования задаются не уравнениями, а неравенствами. Пусть имеется задача линейного программирования с п переменными x 1 , x 2 ,…, x n , в которой ограничения имеют вид линейных неравенств:

a 11 x 1 + a 12 x 2 + . + a 1 n x n + b 1 ≥ 0; a 21 x 1 + a 22 x 2 + . + a 2 n x n + b 2 ≥ 0; . a m 1 x 1 + a m 2 x 2 + . + a mn x n + b m ≥ 0.

Требуется найти такую совокупность неотрицательных значений x 1 , x 2 ,…, x n , которая удовлетворяла бы неравенствам (12.3), и обращала бы в минимум линейную функцию (12.2). От поставленной таким образом задачи можно перейти к основной задаче линейного программирования. Введем обозначения:

y 1	= a 11 x 1 + a 12 x 2 + . + a 1 n x n + b 1 ,
y 2	= a 21 x 1 + a 22 x 2 + . + a 2 n x n + b 2 ,

. y m = a m 1 x 1 + a m 2 x 2 + . + a mn x n + b m ,

где у 1 , у 2 ,…, у т – некоторые новые, добавочные переменные. Согласно условиям (12.3), эти добавочные переменные так же, как x 1 , x 2 ,…, x n , должны быть неотрицательными.

Источник

Свойства основной задачи линейного программирования. Геометрическое истолкование задачи линейного программирования

Рассмотрим основную задачу линейного программирования. Она состоит в определении максимального значения функции при условиях

Перепишем эту задачу в векторной форме: найти максимум функции

(16)

(17)

где , CX – скалярное произведение; и – m-мерные вектор-столбцы, составленные из коэффициентов при неизвестных и свободных членах системы уравнений задачи:

План называется опорным планом, основной задачи линейного программирования, если система векторов , входящих в разложение (16) с положительными коэффициентами линейно независима.

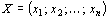
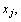
Так как векторы являются m-мерными, то из определения опорного плана следует, что число его положительных компонент не может быть больше, чем т.

Опорный план называется невырожденным, если он содержит ровно т положительных компонент, в противном случае он называется вырожденным. Свойства основной задачи линейного программирования (15) – (17) тесным образом связаны со свойствами выпуклых множеств.

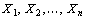
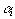
Пусть – произвольные точки евклидова пространства . Выпуклой линейной комбинацией этих точек называется сумма где – произвольные неотрицательные числа, сумма которых равна 1: Множество называется выпуклым, если вместе с любыми двумя своими точками оно содержит и их произвольную выпуклую линейную комбинацию. Точка Х выпуклого множества называется угловой, если она не может быть представлена в виде выпуклой линейной комбинации каких-нибудь двух других различных точек данного множества. Множество планов основной задачи линейного программирования является выпуклым (если оно не пусто). Непустое множество планов основной задачи линейного программирования называется многогранником решений, а всякая угловая точка многогранника решений – вершиной. Если основная задача линейного программирования имеет оптимальный план, то максимальное значение целевая функция задачи принимает в одной из вершин многогранника решений. Если максимальное значение целевая функция задачи принимает более чем в одной вершине, то она принимает его во всякой точке, являющейся выпуклой линейной комбинацией этих вершин.

Если система векторов в разложении (16) линейно независима и такова, что

(18)

где все то точка является вершиной многогранника решений.

Если – вершина многогранника решений, то векторы , соответствующиеположительным в разложении (16), линейно независимы.

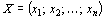
Сформулированные теоремы позволяют сделать следующие выводы.

Непустое множество планов основной задачи линейного программирования образует выпуклый многогранник. Каждая вершина этого многогранника определяет опорный план. В одной из вершин многогранника решений (т. е. для одного из опорных планов) значение целевой функции является максимальным (при условии, что функция ограничена сверху на множестве планов). Если максимальное значение функция принимает более чем в одной вершине, то это же значение она принимает в любой точке, являющейся выпуклой линейной комбинацией данных вершин.

Вершину многогранника решений, в которой целевая функция принимает максимальное значение, найти сравнительно просто, если задача, записанная в форме стандартной, содержит не более двух переменных или задача, записанная в форме основной, содержит не более двух свободных переменных, т. е. , где n – число переменных, r – ранг матрицы, составленной из коэффициентов в системе ограничений задачи.

28. Основные предпосылки, переменные и графики изменения запаса в основной модели управления производственными запасами предприятия и модели производственных поставок. Формулы определения оптимального запаса в моделях.

Рассмотрим для начала проблемы управления запасами, связанные либо с заказом на партию деталей внешнему поставщику, либо с выпуском партии деталей. Политика организации производства или подачи заказов в этой ситуации должна быть такой, чтобы общие издержки были минимальными.

В любой системе управления запасами уровень последних изменяется в соответствии с циклической моделью. Процесс снижения уровня запасов определяется соответствующей моделью спроса. В некоторой точке для пополнения запаса будет сделан новый заказ. По прошествии некоторого времени, называемого временем поставки, заказ будет получен, и уровень запасов возрастает. После этого начинается новый цикл запасов.

Источник

Линейное программирование

Линейное программирование (ЛП) — наука о методах исследования и отыскания экстремальных (наибольших и наименьших) значений линейной функции, на неизвестные которой наложены линейные ограничения.
Эта линейная функция называется целевой, а ограничения, которые математически записываются в виде уравнений или неравенств, называются системой ограничений.
В общем виде математическая модель задачи линейного программирования (ЗЛП) записывается как

где x_j — неизвестные; a_ij, b_i, c_j — заданные постоянные величины.

• ввести обозначения переменных;
• учитывая ограничения в использовании экономических показателей задачи и их количественные закономерности, записать систему ограничений;
• исходя из цели экономических исследований, составить целевую функцию.

Основные свойства задачи линейного программирования

Приведем основные свойства задачи ЛП.
1. Допустимое множество решений задачи ЛП либо пусто, либо является выпуклым многогранником в R n (как пересечение полупространств, описываемых ограничениями-неравенствами). Оно может быть как ограниченным, так и неограниченным; в любом случае это замкнутый многогранник.
2. Если допустимое множество не пусто, а целевая функция ограничена сверху (для задачи максимизации, а для задачи минимизации — ограничена снизу) на этом множестве, то задача ЛП имеет оптимальное решение.
3. Оптимальные решения задачи ЛП (если они существуют) всегда находятся на границе допустимого множества. Точнее, если существует единственное оптимальное решение, то им является какая-либо вершина многогранника допустимых решений; если две или несколько вершин являются оптимальными решениями, то любая их выпуклая комбинация также является оптимальным решением (т.е. существует бесконечно много точек максимума или минимума). Для любой задачи ЛП можно составить двойственную к ней задачу по следующим правилам.
1. Привести исходную задачу ЛП к стандартной форме.
2. Ввести новые переменные по числу основных ограничений исходной задачи.
3. Составить новые ограничения из новых переменных в виде линейных неравенств, знаки которых противоположны знакам неравенств исходной задачи, коэффициентами которых служат элементы транспонированной матрицы исходной задачи, а свободными членами — коэффициенты при целевой функции исходной задачи.
4. Для новых переменных написать условия неотрицательности.
В результате для исходной задачи (5.1) получим следующую двойственную задачу ЛП: (5.3)
Задача (5.1) относительно задачи (5.3) называется прямой задачей ЛП . Векторная форма задачи (5.3) имеет вид: (5.4)
Рассмотрение взаимно двойственных задач ЛП полезно как с теоретической, так и с практической точек зрения. Это видно из следующих утверждений.
1. Если одна из задач (5.1) и (5.3) имеет оптимальное решение, то и другая имеет оптимальное решение, причем
2. Если целевая функция одной из задач неограниченна, то ограничения другой задачи несовместны (т.е. множество допустимых решений пусто).
3. Для того, чтобы допустимое решение и были оптимальными решениями соответствующих задач (5.1) и (2.3) , необходимо и достаточно, чтобы

4. Для любых допустимых решений x 0 и y 0 справедливо неравенство f(x 0 ) ≤ z(y 0 ); если f(x 0 ) = z(y 0 ), то x 0 и y 0 — оптимальные решения задач (5.1) и (5.3).
5. Если прямая задача (5.1) моделирует максимизацию дохода при ограниченных ресурсах, то двойственная задача (5.3) при тех же предпосылках моделирует минимизацию затрат при фиксированном уровне дохода.

Источник