Постановка задачи линейного программирования и свойства ее решений
Линейное программирование — раздел математического программирования, применяемый при разработке методов отыскания экстремума линейных функций нескольких переменных при линейных дополнительных ограничениях, налагаемых на переменные. По типу решаемых задач его методы разделяются на универсальные и специальные. С помощью универсальных методов могут решаться любые задачи линейного программирования(ЗЛП). Специальные методы учитывают особенности модели задачи, ее целевой функции и системы ограничений. Особенностью задач линейного программирования является то, что экстремума целевая функция достигает на границе области допустимых решений. Классические же методы дифференциального исчисления связаны с нахождением экстремумов функции во внутренней точке области допустимых значений. Отсюда — необходимость разработки новых методов. Формы записи задачи линейного программирования: Общей задачей линейного программирования называют задачу 
( 1) при ограничениях 
( 2) 
( 3) 
( 4) 
( 5) 
— произвольные 
( 6) где 
— заданные действительные числа; ( 1) – целевая функция; ( 1) – ( 6) –ограничения; 
— план задачи. Пусть ЗЛП представлена в следующей записи: 
( 7) 
( 8) 
( 9) Чтобы задача ( 7) – ( 8) имела решение, системе её ограничений ( 8) должна быть совместной. Это возможно, еслиrэтой системы не больше числа неизвестныхn. Случайr>nвообще невозможен. Приr=nсистема имеет единственное решение, которое будет при 
оптимальным. В этом случае проблема выбора оптимального решения теряет смысл. Выясним структуру координат угловой точки многогранных решений. Пустьrn. В этом случае система векторов 
содержит базис — максимальную линейно независимую подсистему векторов, через которую любой вектор системы может быть выражен как ее линейная комбинация. Базисов, вообще говоря, может быть несколько, но не более 
.Каждый из них состоит точно изrвекторов. Переменные ЗЛП, соответствующиеrвекторам базиса, называют, как известно,базиснымии обозначают БП. Остальныеn–rпеременных будутсвободными,их обозначают СП. Не ограничивая общности, будем считать, что базис составляют первыеmвекторов 
. Этому базису соответствуют базисные переменные 
, а свободными будут переменные 
. Если свободные переменные приравнять нулю, а базисные переменные при этом примут неотрицательные значения, то полученное частное решение системы (8) называютопорным решением (планом).Теорема. Если система векторов 
содержит m линейно независимых векторов 
, то допустимый план 
( 10) является крайней точкой многогранника планов.Теорема. Если ЗЛП имеет решение, то целевая функция достигает экстремального значения хотя бы в одной из крайних точек многогранника решений. Если же целевая функция достигает экстремального значения более чем в одной крайней точке, то она достигает того же значения в любой точке, являющейся их выпуклой линейной комбинацией.
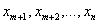
Графический способ решения злп
Геометрическая интерпретация экономических задач дает возможность наглядно представить, их структуру, выявить особенности и открывает пути исследования более сложных свойств. ЗЛП с двумя переменными всегда можно решить графически. Однако уже в трехмерном пространстве такое решение усложняется, а в пространствах, размерность которых больше трех, графическое решение, вообще говоря, невозможно. Случай двух переменных не имеет особого практического значения, однако его рассмотрение проясняет свойства ОЗЛП, приводит к идее ее решения, делает геометрически наглядными способы решения и пути их практической реализации. Пусть дана задача 
( 11) 
( 12) 
( 13) Дадим геометрическую интерпретацию элементов этой задачи. Каждое из ограничений ( 12), ( 13) задает на плоскости 
некоторую полуплоскость. Полуплоскость — выпуклое множество. Но пересечение любого числа выпуклых множеств является выпуклым множеством. Отсюда следует, что область допустимых решений задачи ( 11) — ( 13) есть выпуклое множество. Перейдем к геометрической интерпретации целевой функции. Пусть область допустимых решений ЗЛП — непустое множество, например многоугольник 
. 
Выберем произвольное значение целевой функции 
.Получим 
.Это уравнение прямой линии. В точках прямойNМцелевая функция сохраняет одно и то же постоянное значение 
. Считая в равенстве ( 11) 
параметром, получим уравнение семейства параллельных прямых, называемых линиями уровня целевой функции (линиями постоянного значения). Найдём частные производные целевой функции по 
и 
: 
, ( 14) 
. ( 15) Частная производная ( 14) (так же как и ( 15)) функции показывает скорость ее возрастания вдоль данной оси. Следовательно, 
и 
— скорости возрастания 
соответственно вдоль осей 
и . Вектор 
называется градиентом функции. Он показывает направление наискорейшего возрастания целевой функции: 
Вектор 
указывает направление наискорейшего убывания целевой функции. Его называют антиградиентом. Вектор 
перпендикулярен к прямым 
семейства 
. Из геометрической интерпретации элементов ЗЛП вытекает следующий порядок ее графического решения. 1. С учетом системы ограничений строим область допустимых решений 
. Строим вектор 
наискорейшего возрастания целевой функции — вектор градиентного направления. 3. Проводим произвольную линию уровня 
.4. При решении задачи на максимум перемещаем линию уровня 
в направлении вектора 
так, чтобы она касалась области допустимых решений в ее крайнем положении (крайней точке). В случае решения задачи на минимум линию уровня 
перемещают в антиградиентном направлении. 5. Определяем оптимальный план 
и экстремальное значение целевой функции 
.
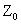
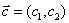
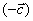
2.3. Свойства решений задачи линейного программирования
Выделим зависимость между m и n и количеством решений системы уравнений.
Пусть m>n. Количество уравнений больше числа переменных и нет линейно-зависимых уравнений. Система не имеет решений.
Если m=n и нет линейно зависимых, то система ограничений имеет единственное решение. Следовательно, ЗЛП имеет единственное решение именно в этой точке.
Запишем ЗЛП в векторном виде:
Область допустимых значений будем называть многогранником планов (для ЗЛП от двух неизвестных – выпуклый многоугольник). Точку пересечения линий будем называть крайней точкой многогранника планов.
Решая ЗЛП, мы получили некоторое решение, удовлетворяющее системе ограничений. Если свободные переменные при этом равны нулю, а базисные переменные принимают неотрицательные значения, то полученное частное решение называют опорным решением.
Теорема1. Если система векторов 
, имеет линейно-независимую подсистему
, то допустимое решение (
,0,0,…,0) является крайней точкой многогранника планов.
Замечание: Среди крайних точек многогранника плана и находится оптимальное (max) решение.
Теорема2. (основная теорема линейного программирования) Если ЗЛП имеет решение, то целевая функция достигает экстремального значения хотя бы в одной из крайних точек многогранника решений. Если же целевая функция достигает экстремального значения более чем в одной крайней точке, то она достигает такого же значения в любой точке, являющейся их выпуклой линейной комбинацией.
2.4. Общая идея симплексного метода
Исходя из основной теоремы линейного программирования, можно предположить следующий метод решения ЗЛП: Находятся все крайние точки многогранника планов и из них выбирается оптимальная. Метод решения универсален, но чрезвычайно трудоемок. Количество крайних точек многогранника планов можно рассчитать по формуле:
.
Для примера: m=5, n=7. Количество крайних точек: 21. каждую из них необходимо найти, посчитать значение целевой функции. Потом все их сравнить.
В связи с этим была поставлена проблема оптимизации перебора точек, т.е. не все точки находить, а только те, значение целевой функции в которых «лучше», чем исходное.
Таким образом, общая идея симплексного метода состоит в следующем: перемещаясь от данной крайней точки к смежной по ребру лучшей, а затем еще лучшей, найти оптимальное решение ЗЛП.
Алгоритм решения ЗЛП симплексным методом:
- Найти начальное опорное решение ЗЛП.
- Проверить, не является ли оно оптимальным.
- Если решение оптимально, то ЗЛП решена. В противном случае необходимо перейти в другую крайнюю точку многогранника планов (найти другое опорное решение), которая не хуже предыдущей (значение целевой функции не хуже, чем в предыдущей точке).
- Перейти к пункту 2.
- уметь строить начальный опорный план ЗЛП;
- знать признак оптимальности опорного плана;
- уметь переходить к нехудшему опорному плану.
2.3. Свойства решений задачи линейного программирования
Выделим зависимость между m и n и количеством решений системы уравнений.
Пусть m>n. Количество уравнений больше числа переменных и нет линейно-зависимых уравнений. Система не имеет решений.
Если m=n и нет линейно зависимых, то система ограничений имеет единственное решение. Следовательно, ЗЛП имеет единственное решение именно в этой точке.
Запишем ЗЛП в векторном виде:
Область допустимых значений будем называть многогранником планов (для ЗЛП от двух неизвестных – выпуклый многоугольник). Точку пересечения линий будем называть крайней точкой многогранника планов.
Решая ЗЛП, мы получили некоторое решение, удовлетворяющее системе ограничений. Если свободные переменные при этом равны нулю, а базисные переменные принимают неотрицательные значения, то полученное частное решение называют опорным решением.
Теорема1. Если система векторов 
, имеет линейно-независимую подсистему
, то допустимое решение (
,0,0,…,0) является крайней точкой многогранника планов.
Замечание: Среди крайних точек многогранника плана и находится оптимальное (max) решение.
Теорема2. (основная теорема линейного программирования) Если ЗЛП имеет решение, то целевая функция достигает экстремального значения хотя бы в одной из крайних точек многогранника решений. Если же целевая функция достигает экстремального значения более чем в одной крайней точке, то она достигает такого же значения в любой точке, являющейся их выпуклой линейной комбинацией.
2.4. Общая идея симплексного метода
Исходя из основной теоремы линейного программирования, можно предположить следующий метод решения ЗЛП: Находятся все крайние точки многогранника планов и из них выбирается оптимальная. Метод решения универсален, но чрезвычайно трудоемок. Количество крайних точек многогранника планов можно рассчитать по формуле:
.
Для примера: m=5, n=7. Количество крайних точек: 21. каждую из них необходимо найти, посчитать значение целевой функции. Потом все их сравнить.
В связи с этим была поставлена проблема оптимизации перебора точек, т.е. не все точки находить, а только те, значение целевой функции в которых «лучше», чем исходное.
Таким образом, общая идея симплексного метода состоит в следующем: перемещаясь от данной крайней точки к смежной по ребру лучшей, а затем еще лучшей, найти оптимальное решение ЗЛП.
Алгоритм решения ЗЛП симплексным методом:
- Найти начальное опорное решение ЗЛП.
- Проверить, не является ли оно оптимальным.
- Если решение оптимально, то ЗЛП решена. В противном случае необходимо перейти в другую крайнюю точку многогранника планов (найти другое опорное решение), которая не хуже предыдущей (значение целевой функции не хуже, чем в предыдущей точке).
- Перейти к пункту 2.
- уметь строить начальный опорный план ЗЛП;
- знать признак оптимальности опорного плана;
- уметь переходить к нехудшему опорному плану.