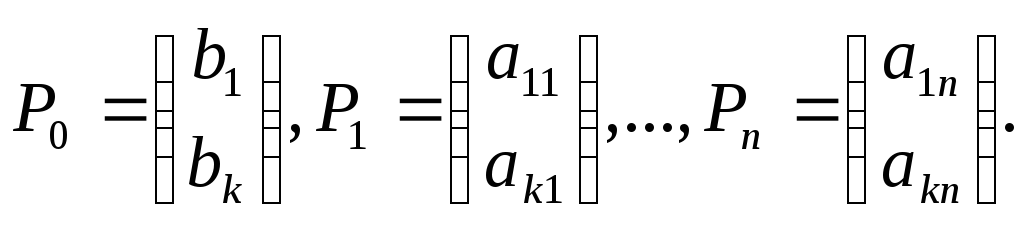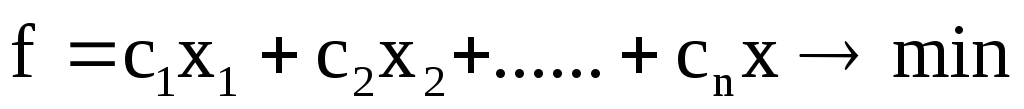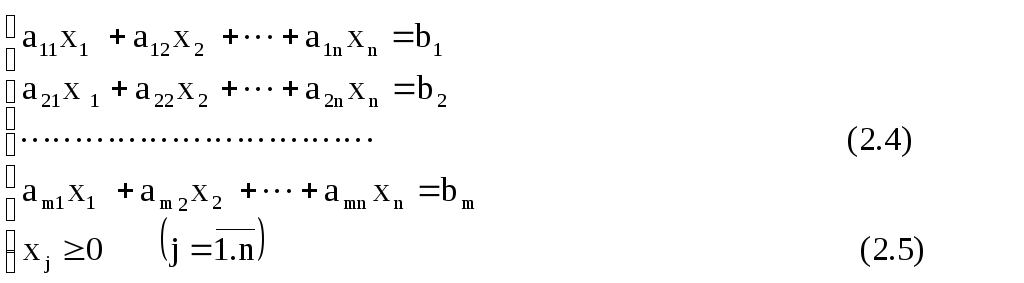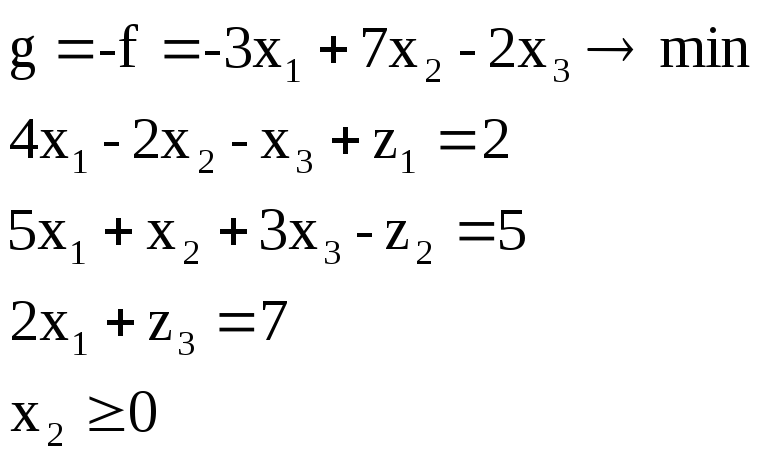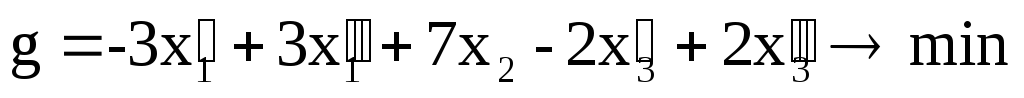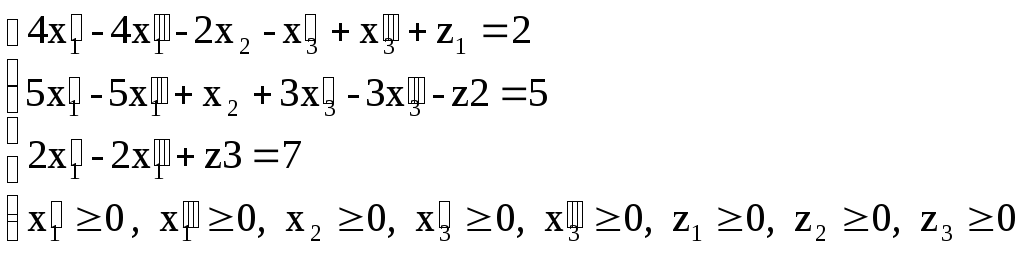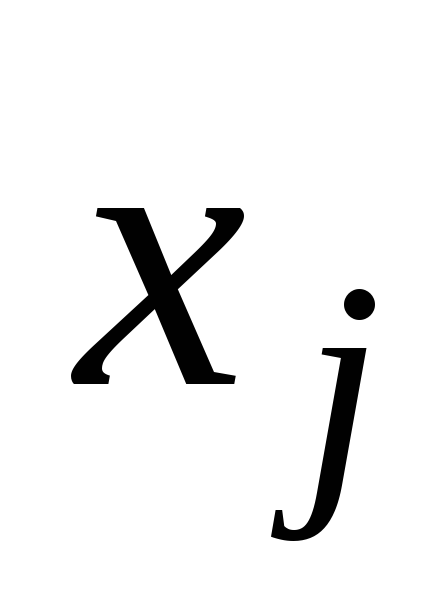Свойства канонической задачи линейного программирования

2.6. Канонический вид злп.

В исходной постановке ЗЛП могут допускать различные формы записи. Так, в одних задачах требуется максимизировать целевую функцию, в других — минимизировать; некоторые линейные ограничения могут иметь вид равенств, другие — неравенств и т.д.

Для единообразия записи ЗЛП вводится так называемая каноническая форма записи.

Говорят, что ЗЛП записана в канонической форме, если она имеет следующий вид:

(2.3)

Отметим следующие особенности канонического вида:

1) требуется минимизировать целевую функцию;

2) все линейные ограничения, кроме требований неотрицательности переменных, имеют вид равенств;

1. на все переменные наложены требования неотрицательности.

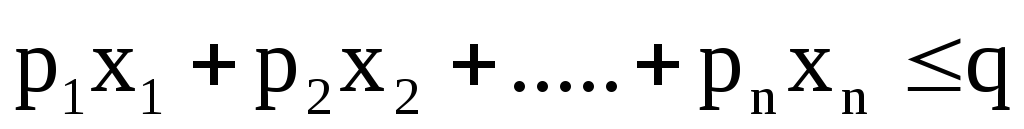
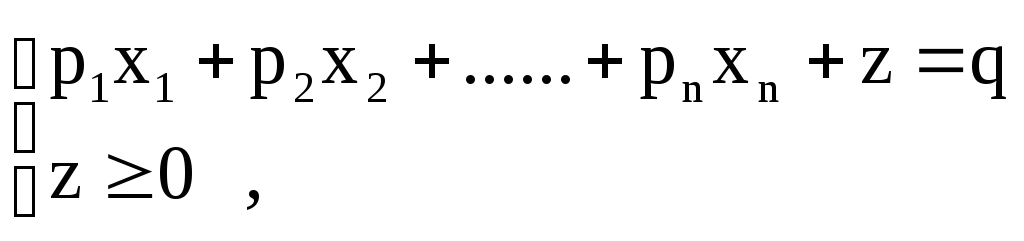
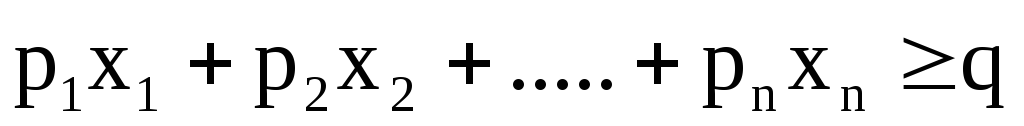
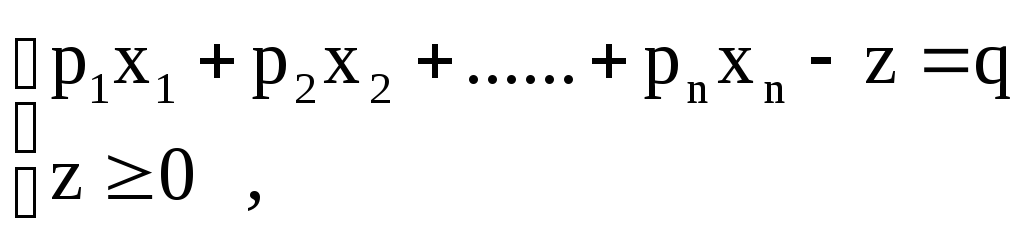
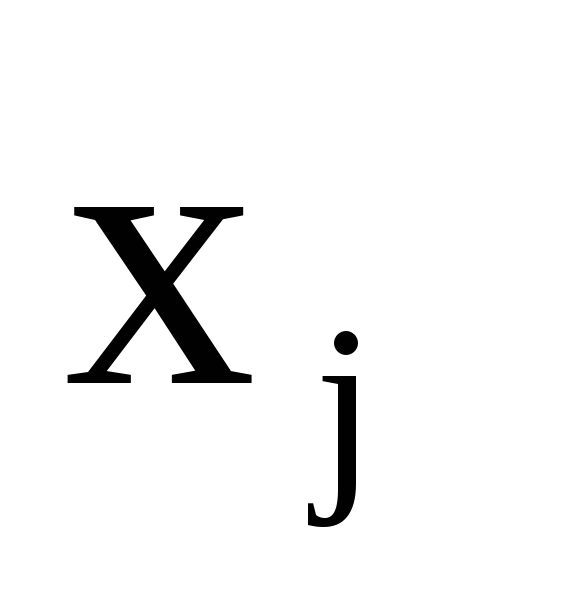
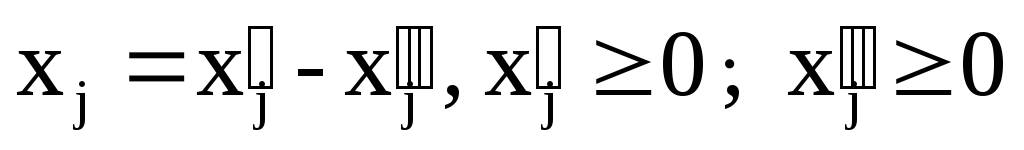
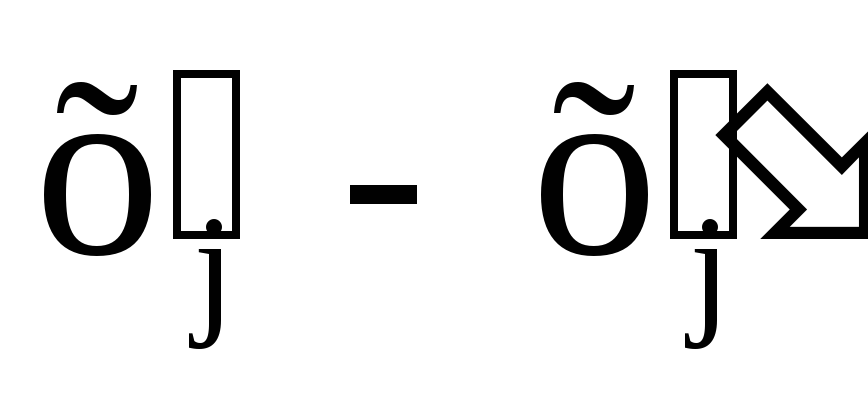
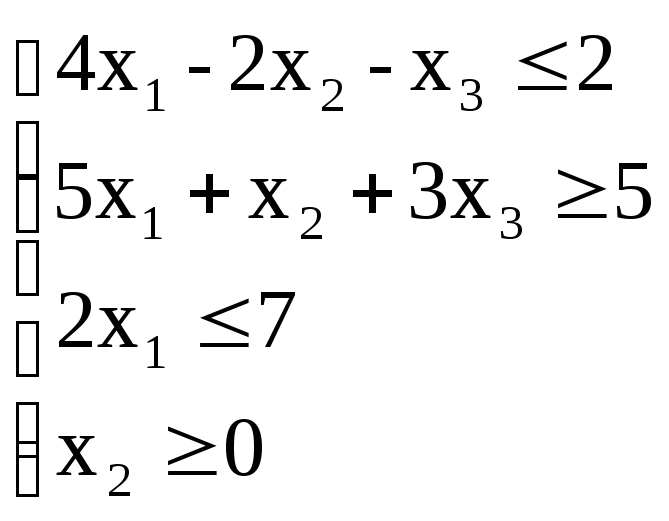
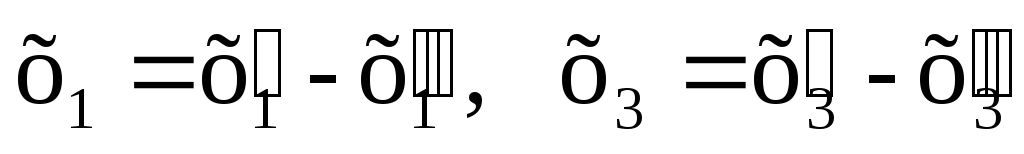
Покажем, что любую ЗЛП можно привести к каноническому виду. 1) Если в ЗЛП требуется максимизировать целевую функцию f, то положим g = — f и потребуем минимизировать функцию g. Получится новая ЗЛП, которая эквивалентна исходной в том смысле, что каждое оптимальное решение исходной задачи будет оптимальным решением новой задачи и наоборот. 2) Предположим, что в ЗЛП есть линейное ограничение вида . Заменим такое ограничение следующими двумя ограничениями: где z— новая переменная, которая в целевую функцию вводится с коэффициентом 0 (иначе говоря, переменная z не вводится в целевую функцию). Значение переменной z можно не учитывать после решения новой задачи. Аналогично, ограничение вида заменяется двумя ограничениями: 3) Предположим, что в ЗЛП не ко всем переменным предъявлено требование неотрицательности. Тогда каждую, переменную , на которую не наложено требование неотрицательности, представим в виде разности двух неотрицательных переменных: (2.6) Каждое вхождение переменной в целевую функцию или ограничения заменим разностью. Решив новую задачу с помощью (2.6), вернемся к прежним переменным. Указанными приемами любая ЗЛП приводится к каноническому виду. Пример. Привести к каноническому виду Проделаем описанные действия. Теперь получим ЗЛП в каноническом виде:

2.7. Понятие опорного плана злп.

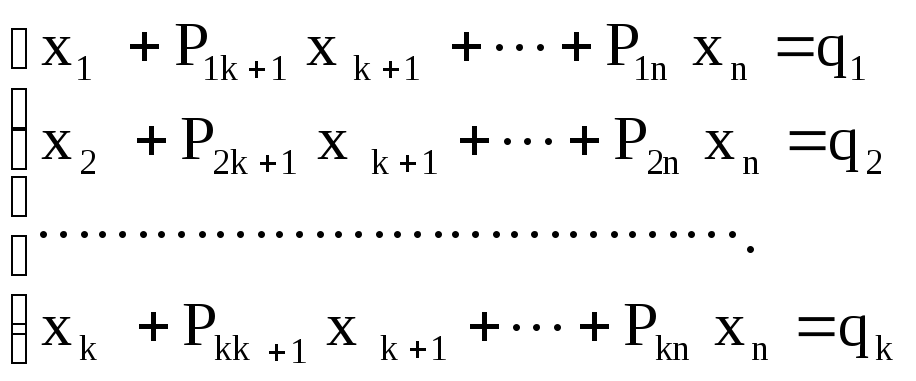
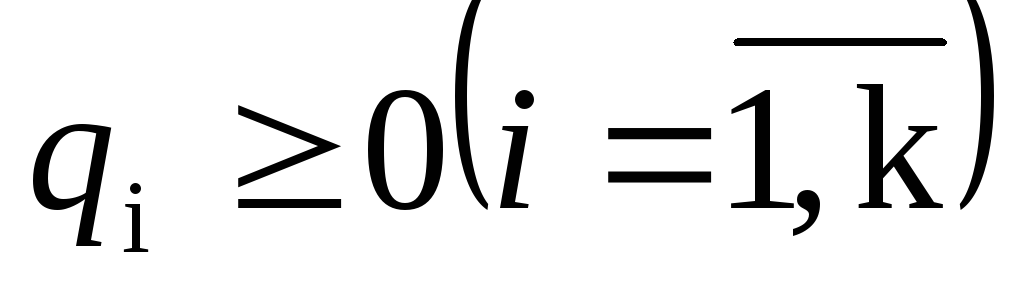
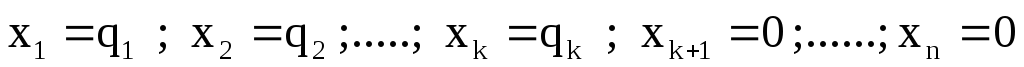
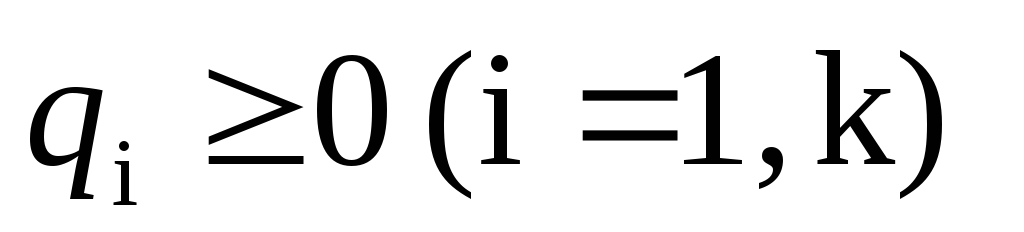
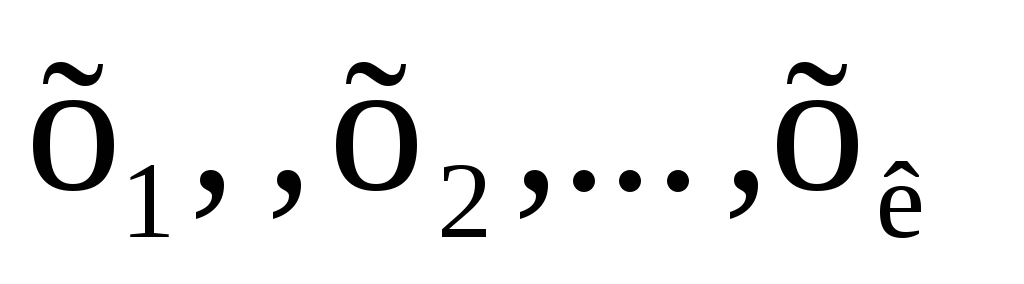
Пусть ВЛП задана в каноническом виде (2.3 — 2.5). Предположим, что система уравнений (2.4) приведена к жордановой форме с неотрицательными правыми частями: (2.6) где . Приравняв к нулю свободные переменные, получим базисное решение системы (2.4) (2.7) В силу условия набор значений переменных (2.7) удовлетворяет и ограничениям (2.5). Поэтому (2.6) являетсядопустимым решением ЗЛП. Допустимое решение (2.7) называется базисным допустимым решением или опорным планом ЗЛП. При этом говорят, что переменные образуют допустимый базис. Оказывается, что если ОДР изобразить геометрически, то каждый опорный план ЗЛП соответствует вершине многогранника. Поэтому справедлива следующая теорема. Если ЗЛП разрешима, то существует оптимальный опорный план.

3. Симплексный метод решения злп

3.1. Общая характеристика и основные этапы симплекс – метода

Основоположниками симплекс-метода являются советский математик Л.В. Канторович и американский математик Дж. Данциг. Симплекс-методом можно решить любую ЗЛП или обнаружить ее неразрешимость. Многие специальные классы ЗЛП можно решить другими, более эффективными для этих классов методами. Однако преимущество симплекс-метода — его универсальность. Почти для всех ЭВМ разработаны стандартные программы для решения ЗЛП симплекс — методом. Опишем общую идею симплекс-метода. Считаем, что ЗЛП записана в каноническом виде и целевую функцию нужно минимизировать. Как мы уже знаем, оптимальный план следует искать среди опорных планов ЗЛП. Симплекс-метод не перебирает все опорные планы (что было бы часто невозможно из-за их огромного количества), а, начиная с некоторого исходного опорного плана, он последовательно переходит к другим опорным планам с уменьшением целевой функции. Симплекс-метод прекращает свою работу тогда, когда либо будет найден оптимальный опорный план, либо установлена неразрешимость задачи. При решении ЗЛП симплекс-методом можно выделить следующие этапы: 1) приведение ЗЛП к каноническому виду; 2) приведение системы линейных уравнений к жордановой форме с неотрицательными правыми частями с одновременной проверкой на неразрешимость ЗЛП из-за противоречивости системы линейных ограничений; 3) исследование опорного плана на оптимальность; 4) исследование ЗЛП на неразрешимость из-за неограниченности снизу на ОДР целевой функции; 5) переход к новому, «лучшему» опорному плану.

Источник

4.1. Каноническая форма задачи линейного программирования

Запись целевой функции и системы ограничений в различных задачах линейного программирования неодинаков: в одних задачах требуется найти минимум целевой функции, а в других – максимум; в одних случаях искомые переменные зависят от одного индекса, а в других – от двух; в одних задачах ограничения заданы в виде системы линейных неравенств, а в других – в виде системы линейных уравнений. На практике возможны также задачи, в которых часть ограничений имеет вид линейных неравенств, а часть – линейных уравнений. Также не во всех задачах может требоваться неотрицательность переменных .

Учет такого разнообразия задач линейного программирования требует разработки специальных методов для решения отдельных их классов. Мы же сосредоточим свое внимание на изучении общих свойств и методов линейного программирования, записанных в так называемой канонической форме.

Если в задаче линейного программирования система исходных ограничений приобретает вид уравнений типа

или

и нужно найти максимум линейной целевой функции

,

то считается, что задача линейного программирования записана в канонической форме.

Любую задачу линейного программирования можно легко свести к канонической форме. В общем случае для этого достаточно уметь, во-первых, свести задачу минимизации целевой функции к задаче ее максимизации, во-вторых, переходить от ограничений-неравенств к ограничениям-равенствам, и в-третьих, менять те переменные, которые не подчинены условию неотрицательности.

В том случае, когда нужно найти минимум функции , можно перейти к нахождению максимума функции , поскольку справедливо утверждение: .

Ограничение-неравенство исходной задачи, которое имеет вид «» , можно превратить в ограничение-уравнение путем добавления к его левой части дополнительной неотрицательной переменной, а ограничение-неравенство вида «»– путем вычитания из его левой части дополнительной неотрицательной переменной.

Заметим, что количество введенных дополнительных неотрицательных переменных всегда равно количеству неравенств в исходной системе ограничений.

Введены дополнительные переменные имеют вполне конкретный экономический смысл. Так, если в ограничениях исходной задачи линейного программирования отражаются расходы и наличие производственных ресурсов, то числовое значение дополнительной переменной показывает объем соответствующего неиспользованного ресурса.

Отметим также, что если некоторая переменная не подчиняется условию неотрицательности, то ее нужно заменить двумя неотрицавтельными переменными и , приняв .

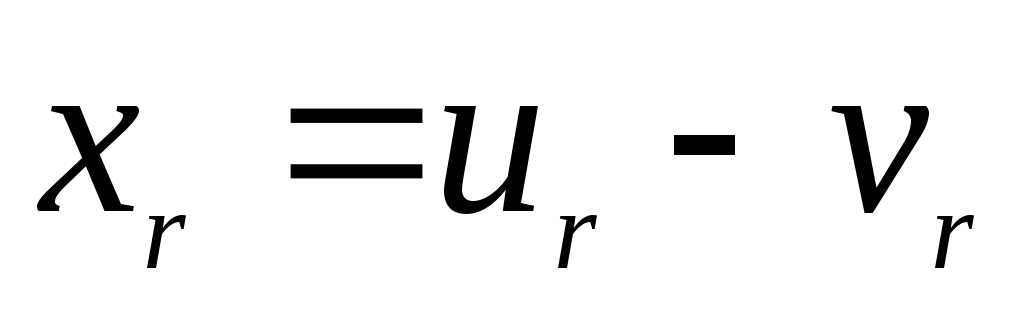
Пример. Записать в канонической форме следующую задачу линейной оптимизации: найти минимум функции при ограничениях

В данной задаче нужно найти минимум целевой функции, а система ограничений включает четыре неравенства. Для того, чтобы записать ее в канонической форме, нужно перейти от ограничений-неравенств к ограничениям-уравнениям, а также превратить целевую функцию.

Так как количество неравенств, входящих в систему ограничений задачи , равно четырем, то этот переход должен быть осуществлен с введением четырех дополнительных неотрицательных переменных. При этом во втором и четвертом неравенствах стоит знак «» , поэтому к их левой части дополнительные переменные добавляем. В первом и третьем неравенствах – знак «», значит от их левой части дополнительные переменные вычитаем.

Также превращаем целевую функцию, поменяв все знаки на противоположные, и находим ее максимум.

Таким образом, данная задача линейного программирования будет записана в следующем каноническом виде:

найти максимум функции

при ограничениях

Источник

Общая и основная задачи линейного программирования.

Общая задача. Найти максимальное значение линейной целевой функции. z = c₁x₁+ c₂x₂+ … + c_nx_n при линейных ограничениях x_j>= 0,j= 1,n= n> Определение 1.1. Совокупность чисел х = (х₁, х₂. х_n), удовлетворяющих ограничениям (1.2), называется допустимым решением или планом. Определение 1.2. План х* =(х₁ * , х₂ * . х_n*), при котором целевая функция (1.1) принимает свое максимальное значение, называется оптимальным.Каноническая форма. Задачу линейного программирова­ния будем считать приведенной к каноническому виду, если 1) требуется найти максимум целевой функции; 2) система ограничений (1.2) содержи! только равенства; 3) правые части системы ограничений неотрицательны. Переход от общей формы к канонической: 1) если в задаче требуется найти минимум целевой функции, то вводим новую целевую функцию z₁ = -z, тогда max z₁ = -min z; 2) чтобы перейти от неравенства к равенству в системе огра­ничений, необходимо прибавить (вычесть) дополнительную не­отрицательную переменную к левой части неравенства; 3) если в правой части системы ограничений имеются отрица­тельные числа, то необходимо умножить на «-1» обе части равен­ства, в котором в правой части стоит отрицательное число. Задачу линейного программирования в канонической фор­ме называют основной задачей.

Свойства задач линейного программирования. Графический метод решения задач линейного программирования.

Свойства задач линейного программирования. Рассмотрим следующую основную задачу линейного про­граммирования: z = c₁x₁+ c₂x₂+ …+c_nx_nmax при ограничениях , Перепишем ограничения этой задачи к немирной форме: x₁Р,+х₂Р₂+. + х_nР_n,(1.3) где Р₁, . Р_nи Р₀ — k-мерные вектор-столбцы, составленные из коэффициентов при неизвестных и свободных членах системы ограничений основной задачи: Определение 1. План х = (x₁,х₂. х_n) называется опорным планом основной задачи линейного программирования, если его положительные коэффициенты (х_j >0) стоят при линейно независимых векторах Р_j. Так как векторы Р: являются k-мерными, то из определения опорного плана следует, что число его положительных компо­нент не может быть больше числа К. Определение 2. Опорный план называется невырож­денным, если он содержит ровно k положительных компонент, в противном случае он называется вырожденным. Свойства задач линейного программирования тесным обра­зом связаны со свойствами выпуклых множеств. Определение 3. Пусть х(|). х(m) — произвольные точ­ки евклидова пространства Rn . Выпуклой линейной комбинацией этих точек называется сумма: а,х(|) + . + а_mх(m) , где а_i; -про­извольные неотрицательные числа, сумма которых равна 1. Определение 4. Множество называется выпуклым, ес­ли вместе с любыми двумя своими точками оно содержит и отре­зок прямой, соединяющий эти точки. Определение 5. Точка х выпуклого множества назы­вается угловой, если она не может быть представлена в виде вы­пуклой линейной комбинации каких-нибудь двух других различ­ных точек данного множества. Сформулируем первое свойство задач ЛП. Теорема 1.1. Множество планов любой задачи линейного программирования является выпуклым (если оно не пусто). Определение 7. Непустое множество планов задачи линейного программирования называется многогранником реше­ний, а всякая угловая точка многогранника решений — вершиной. Сформулируем второе свойство задач ЛП. Теорема 1.2. Если задача линейного программирования имеет оптимальный план, то экстремальное значение целевая функция задачи принимает в одной из вершин многогранника решений. Если экстремальное значение целевая функция прини­мает более чем в одной вершине, то она принимает его на ребре (грани), содержащем эти вершины. Теорема 1.3. Если система векторов Р₁. Р_m() ли­нейно независима и такова, что х₁Р₁₊. + х_mР_m=Р₀, где все х_j>= 0, то точка х = (х,, х₂. х_т,0. 0) является верши­ной многогранника решений. Теорема 1.4. Если х = (х,,х₂. х_п) — вершина многогран­ника решений, то векторы Р_j , соответствующие положительным х_j > 0, линейно независимы.

Источник

Читайте также:  Разработка интернет приложений это