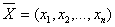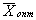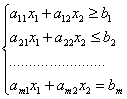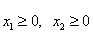Свойства допустимого множества задачи линейного программирования

Нулевые переменные невырожденного опорного решения называются свободными.

Матрица, состоящая из векторов при положительных компонентах невырожденного опорного плана, называется базисной.

Базисное решение – решение системы уравнений (2) , если вектора условий при его ненулевых компонентах линейно-независимые.

Базисная матрица – матрица из линейно-независимых векторов условий, содержащая все вектора условий при ненулевых компонентах. Она всегда квадратная.

Базисная матрица невырожденного решения определяется однозначно, а базисная матрица вырожденного – неоднозначно.

Для определения базисного решения нужно выбрать произвольные переменных , вычислить определитель B из векторов условий этих переменных. Если , то занулить остальные переменные. Тогда для базисных переменных получим систему уравнений:

Максимальное количество базисных решений равно .

Опорное решение – допустимое базисное решение. Для поиска опорных решений можно перебрать все базисные решения и выбрать из них допустимые (с неотрицательными компонентами).

Теорема 3: опорные решения задачи ЛП совпадают с угловыми точками области допустимых решений.

Доказательство теоремы смотри в [8].

Источник

Линейное программирование

Линейное программирование (ЛП) — наука о методах исследования и отыскания экстремальных (наибольших и наименьших) значений линейной функции, на неизвестные которой наложены линейные ограничения.
Эта линейная функция называется целевой, а ограничения, которые математически записываются в виде уравнений или неравенств, называются системой ограничений.
В общем виде математическая модель задачи линейного программирования (ЗЛП) записывается как

где x_j — неизвестные; a_ij, b_i, c_j — заданные постоянные величины.

• ввести обозначения переменных;
• учитывая ограничения в использовании экономических показателей задачи и их количественные закономерности, записать систему ограничений;
• исходя из цели экономических исследований, составить целевую функцию.

Основные свойства задачи линейного программирования

Приведем основные свойства задачи ЛП.
1. Допустимое множество решений задачи ЛП либо пусто, либо является выпуклым многогранником в R n (как пересечение полупространств, описываемых ограничениями-неравенствами). Оно может быть как ограниченным, так и неограниченным; в любом случае это замкнутый многогранник.
2. Если допустимое множество не пусто, а целевая функция ограничена сверху (для задачи максимизации, а для задачи минимизации — ограничена снизу) на этом множестве, то задача ЛП имеет оптимальное решение.
3. Оптимальные решения задачи ЛП (если они существуют) всегда находятся на границе допустимого множества. Точнее, если существует единственное оптимальное решение, то им является какая-либо вершина многогранника допустимых решений; если две или несколько вершин являются оптимальными решениями, то любая их выпуклая комбинация также является оптимальным решением (т.е. существует бесконечно много точек максимума или минимума). Для любой задачи ЛП можно составить двойственную к ней задачу по следующим правилам.
1. Привести исходную задачу ЛП к стандартной форме.
2. Ввести новые переменные по числу основных ограничений исходной задачи.
3. Составить новые ограничения из новых переменных в виде линейных неравенств, знаки которых противоположны знакам неравенств исходной задачи, коэффициентами которых служат элементы транспонированной матрицы исходной задачи, а свободными членами — коэффициенты при целевой функции исходной задачи.
4. Для новых переменных написать условия неотрицательности.
В результате для исходной задачи (5.1) получим следующую двойственную задачу ЛП: (5.3)
Задача (5.1) относительно задачи (5.3) называется прямой задачей ЛП . Векторная форма задачи (5.3) имеет вид: (5.4)
Рассмотрение взаимно двойственных задач ЛП полезно как с теоретической, так и с практической точек зрения. Это видно из следующих утверждений.
1. Если одна из задач (5.1) и (5.3) имеет оптимальное решение, то и другая имеет оптимальное решение, причем
2. Если целевая функция одной из задач неограниченна, то ограничения другой задачи несовместны (т.е. множество допустимых решений пусто).
3. Для того, чтобы допустимое решение и были оптимальными решениями соответствующих задач (5.1) и (2.3) , необходимо и достаточно, чтобы

4. Для любых допустимых решений x 0 и y 0 справедливо неравенство f(x 0 ) ≤ z(y 0 ); если f(x 0 ) = z(y 0 ), то x 0 и y 0 — оптимальные решения задач (5.1) и (5.3).
5. Если прямая задача (5.1) моделирует максимизацию дохода при ограниченных ресурсах, то двойственная задача (5.3) при тех же предпосылках моделирует минимизацию затрат при фиксированном уровне дохода.

Источник

Свойства допустимого множества и оптимального решения в задаче ЛП

Математическая модель ЗЛП может быть канонической и неканонической.

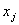
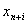
Если все ограничения системы заданы уравнениями и переменные неотрицательные, то такая модель задачи называется канонической. Если хотя бы одно ограничение является неравенством, то модель ЗЛП является неканонической. Чтобы прейти от неканонической модели к канонической, необходимо в каждое неравенство ввести балансовую переменную . Если знак неравенства ≤, то балансовая переменная вводится со знаком +, если знак неравенства ≥, то со знаком -. В целевую функцию балансовые переменные не вводятся.

Свойства допустимого множества и оптимального решения в задаче ЛП.

Определение. Допустимым планом (допустимым решением) задачи линейного программирования называется вектор , удовлетворяющий системе ограничений. Множество допустимых решений образует область допустимых решений.

Допустимое решение, при котором целевая функция достигает своего экстремального значения, называется оптимальным решением ЗЛП и обозначается .

1.Выпуклые множества в n-мерном пространстве.

Рассмотрим на плоскости Х₁ОХ₂ совместную систему линейных неравенств

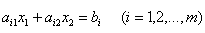
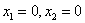
Каждое неравенство этой системы геометрически определяет полуплоскость с граничной прямой . Условия неотрицательности определяют полуплоскости соответственно с граничными прямыми . Система совместна, поэтому полуплоскости как выпуклые множества, пересекаясь, образуют общую часть, которая является выпуклым множеством и представляет собой совокупность точек, координаты каждой из которых являются решением данной системы. Совокупность этих точек называется многоугольником решений. Он может быть точкой, отрезком, лучом, многоугольником, неограниченной многоугольной областью.

2.Свойства решений задачи линейного программирования.

Теорема 1. Множество всех планов задачи линейного программирования выпукло.

Теорема 2. Целевая функция задачи линейного программирования может достигать экстремального значения только в угловой точке области допустимых решений.

Таким образом, для нахождения оптимального решения задачи линейного программирования нет необходимости перебирать все допустимые решения, а достаточно ограничиться перебором лишь конечного числа возможных решений угловых точек многоугольника.

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:

Источник