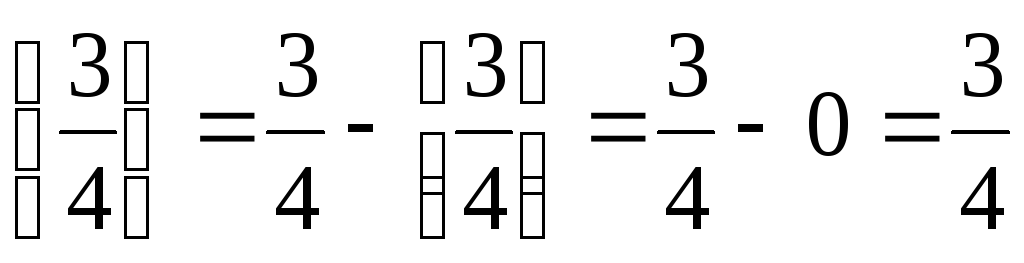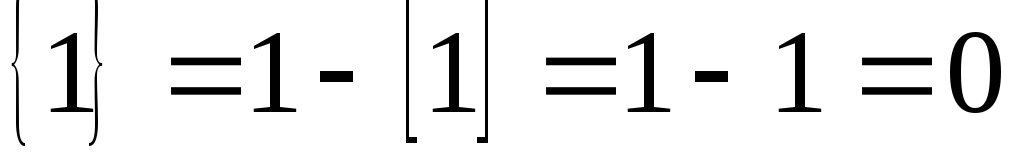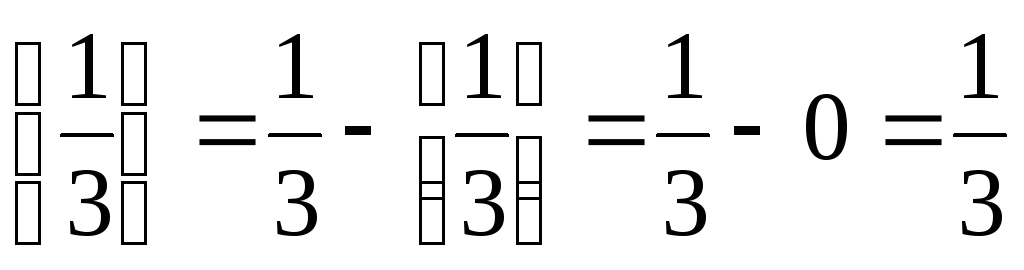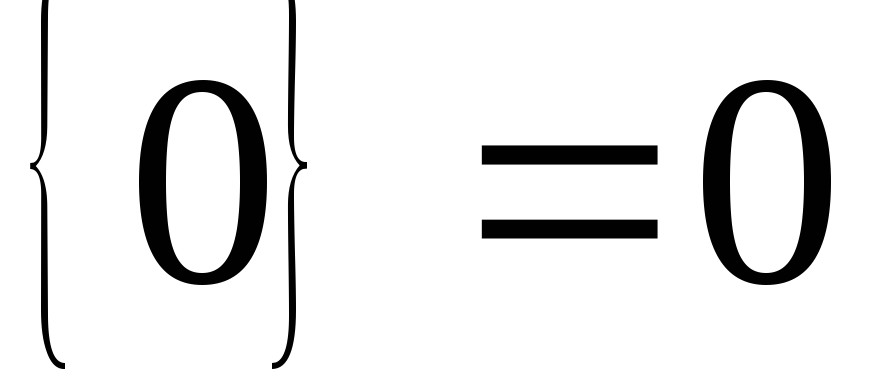Главная » Программирование

Суть метода гомори решения задач целочисленного программирования

Метод Гомори

Метод Гомори решения задач целочисленного программирования является методом отсечения.

Суть метода заключается в построении ограничений, отсекающих нецелочисленные решения задачи линейного программирования, но не отсекающих ни одного целочисленного плана. Для этого сначала решается ослабленная задача линейного программирования без учета условия целочисленности переменных.

Если полученное решение задачи линейного программирования является целочисленным, то задача целочисленного программирования также решена и найденное решение является оптимальным и для нее. Если же в найденном решении задачи линейного программирования одна или большее число переменных не целые, то для отыскания целочисленного решения задачи добавляются новое линейное ограничение, которое отсекает нецелочисленные решения. При продолжении решения расширенной задачи двойственным симплексным методом с учетом этого ограничения получается целочисленный план.

Для нахождения целочисленного решения задачи методом Гомори используется следующий алгоритм.

  1. Решаем ослабленную задачу симплексным методом без учета условия целочисленности. Если все компоненты оптимального плана целые, то он является оптимальным и для задачи целочисленного программирования. Если обнаруживается неразрешимость задачи, то и неразрешима задача целочисленного программирования.
  2. Если в результате решения задачи линейного программирования в полученном оптимальном плане есть нецелая базисная переменная, то к ограничениям задачи добавляется новое ограничение, обладающее следующими свойствами:

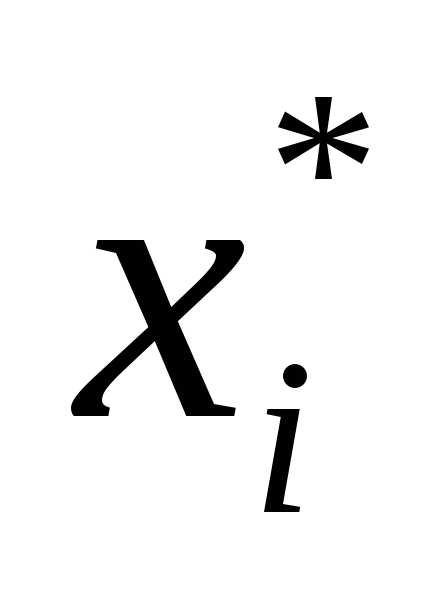
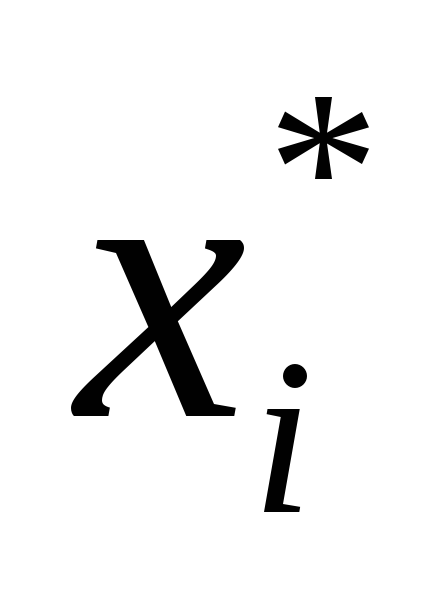
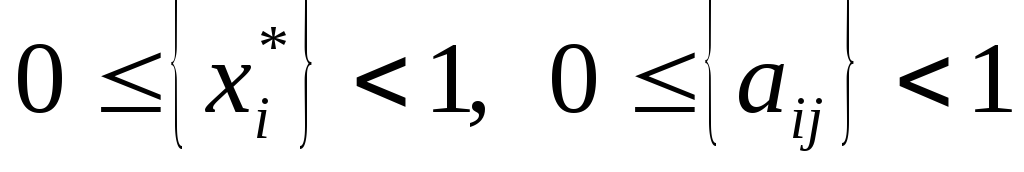
— оно должно быть линейным; — должно отсекать найденный оптимальный нецелочисленный план; — не должно отсекать ни одного целочисленного плана. Если нецелых базисных переменных несколько, то для составления ограничения выбираем компоненту оптимального плана с наибольшей дробной частью (если таких переменных несколько, то выбираем любую). Этой переменной соответствует строка симплексной таблицы, называемая строкой, производящей отсечение (производящей строкой). Для изложения метода вводим следующие понятия. Пусть a – действительное число. Под целой частью некоторого числа а понимается максимальное целое число [a], не превосходящее данного. Под дробной частью некоторого числа а понимается наименьшее неотрицательное число такое, что разность между ним иа есть [a] – целая часть числа). Для выбранной базисной переменной с наибольшей дробной частью находим дробную часть этой переменной и дробные части всех коэффициентов при переменныхi — й строки системы ограничений (производящей строкой). Обозначим ицелые части чисел и . Величины дробных частейи() определяются следующим образом

  1. Составляем неравенство Гомори и включаем его в систему ограничений исходной задачи.
Читайте также:  Языка программирование мобильных приложении java

Для этого по производящей строке симплексной таблицы выписывается уравнение, предполагая, что первые m переменных являются базисными для данного оптимального плана или Переносим все целые части коэффициентов в одну сторону, оставляя все дробные в другой: Так как , получим строгое неравенство Так как левая часть неравенства должна принимать целые значения, то, следовательно, необходимое условие ее целочисленности можно записать только в следующем виде:

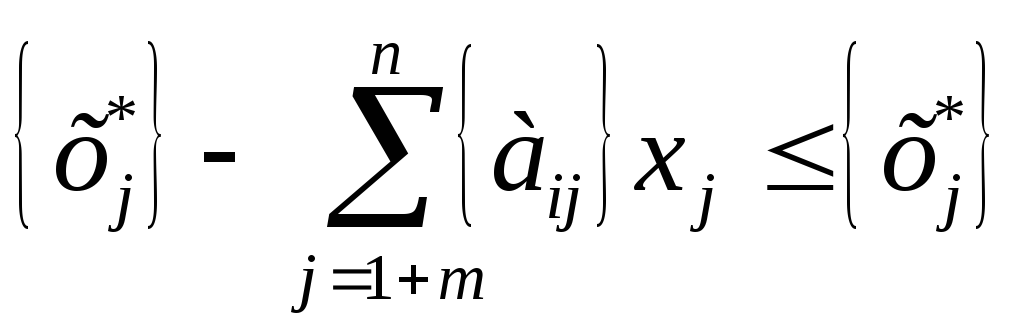
  1. Неравенство преобразуется в уравнение путем введения дополнительной неотрицательной переменной и включается в оптимальную симплексную таблицу.
  2. Решаем задачу, используя двойственный симплексный метод. Если новый оптимальный план расширенной задачи будет целочисленным, то задача решена. Если же решение нецелое, то нужно повторять алгоритм метода Гомори вплоть до получения целочисленного решения.

Пример. Методом Гомори найти решение задачи целочисленного программирования, состоящей в определении максимального значения функции при условии Решение. Выравнивая неравенства с помощью вспомогательных переменных х3, х4, получаем задачу линейного программирования в канонической форме: Решаем задачу линейного программирования симплексным методом, используя поэтапный переход от одного базиса к другому. Ход решения задачи и полученное оптимальное решение представлены в таблицах.

Б СБ В С1=5 С2=11 С3=0 С4=0
а1 а2 а3 а4
а3 0 3 4 1 0
а4 0 10 2 5 0 1
∆j=Zj–Сj 0 -5 -11 0 0
СБ В С1=5 С2=11 С3=0 С4=0
а1 а2 а3 а4
а2 11 1 0
а4 0 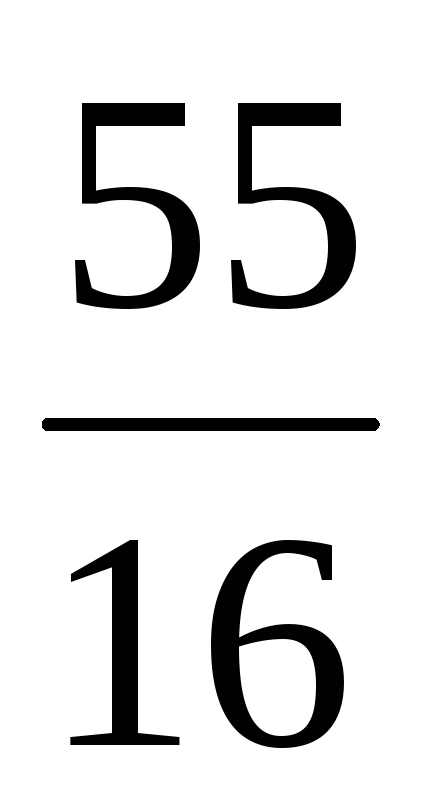0 1
∆j=Zj–Сj 0 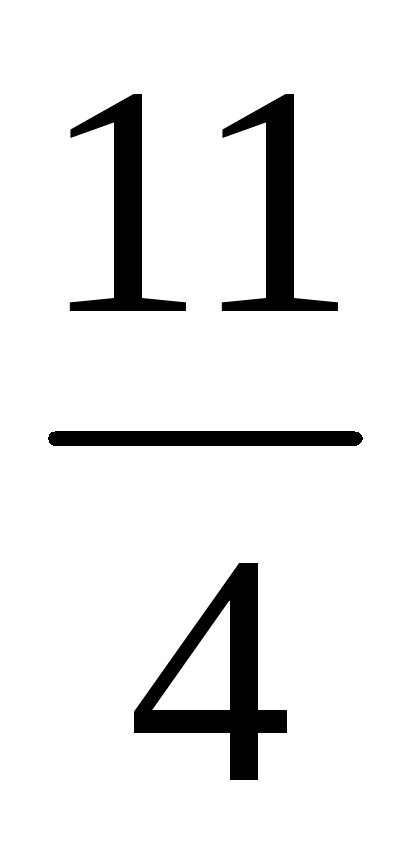0

В найденном оптимальном плане значение переменной х2 равно дробному числу. Находим его дробную часть и дробные части всех элементов строки, содержащей переменную х2 , а именно: Теперь составляем для найденных значений дробных частей неравенство Гомори: . Выравниваем неравенство Гомори с помощью новой вспомогательной переменной х5, переносим свободный член уравнения в правую часть и получаем новое ограничение: . Добавляем в симплексную таблицу строку, содержащую новое ограничение, и столбец, содержащий новую переменную, и продолжаем решать задачу двойственным симплексным методом, так как теперь в таблице записан псевдоплан.

Читайте также:  Программирование си оператор while
Б СБ В С1=5 С2=11 С3=0 С4=0 С5=0
а1 а2 а3 а4 а5
а2 110 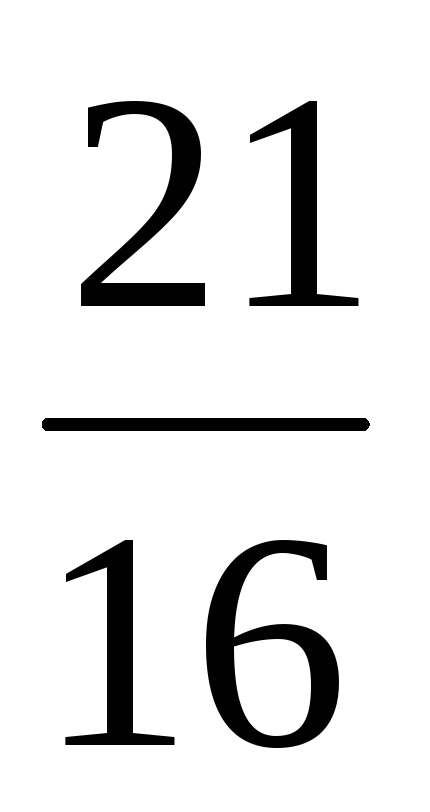1 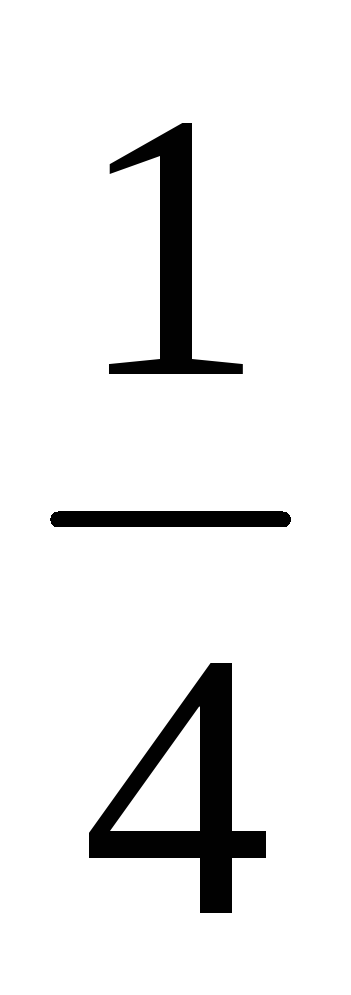0 0
а4 0 0 1 0
а5 0 0 0 1
∆j =Zj–Сj 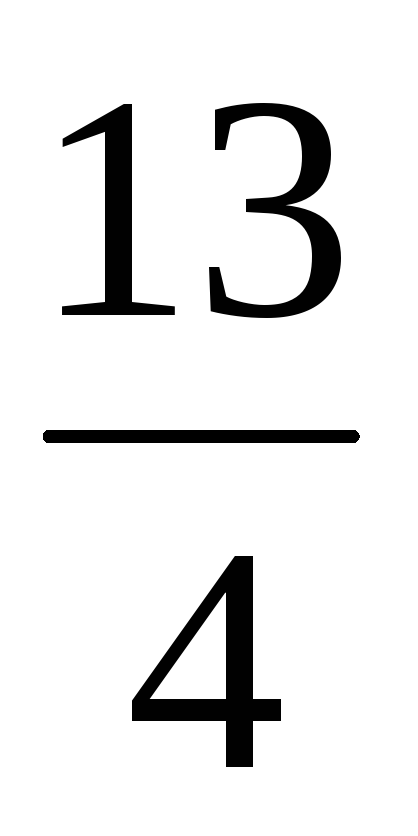0 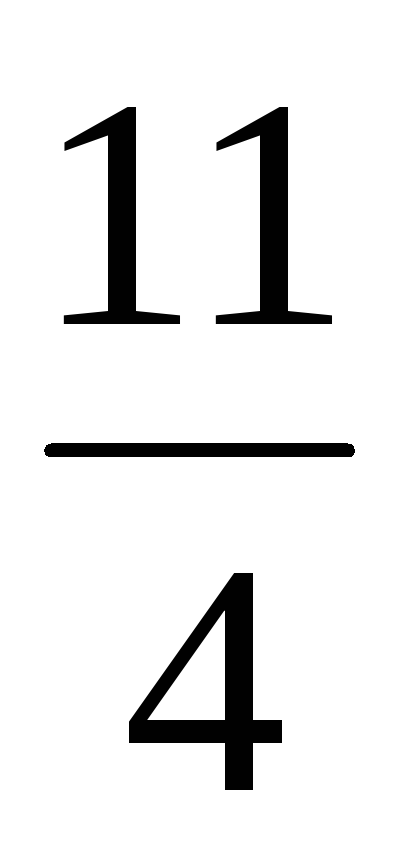0 0
Б СБ В С1=5 С2=11 С3=0 С4=0 С5=0
а1 а2 а3 а4 а5
а2 11 1 0 1 0 0 1
а4 0 0 0 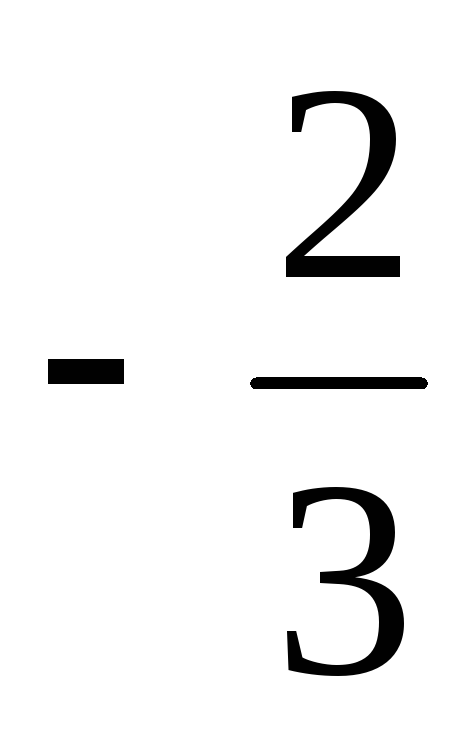1
а1 0 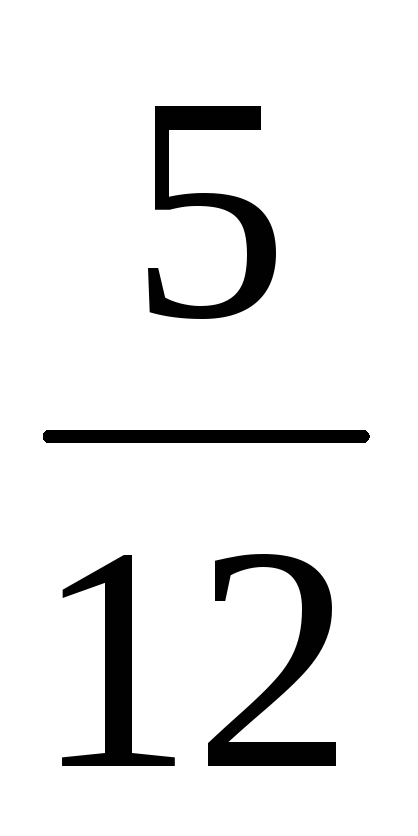1 0 0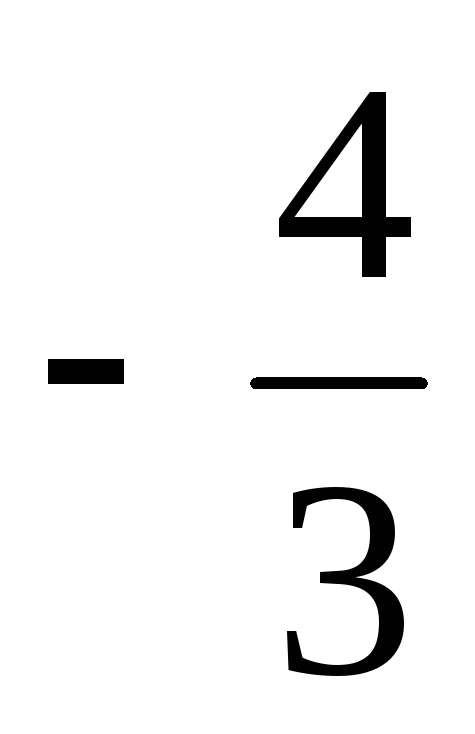
∆j =Zj–Сj 0 0 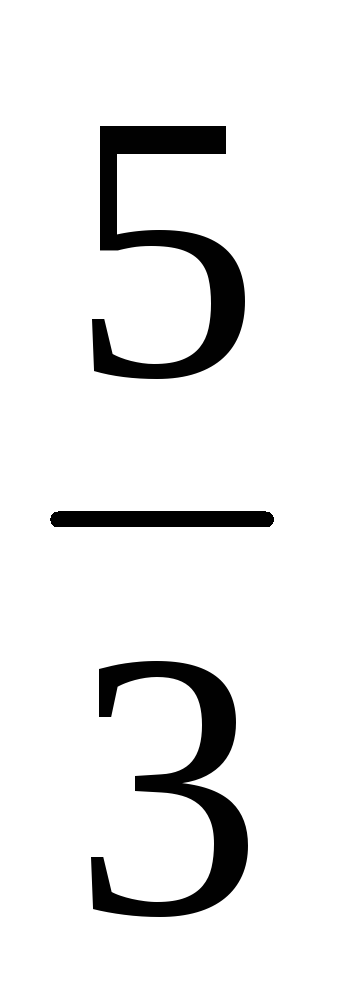0

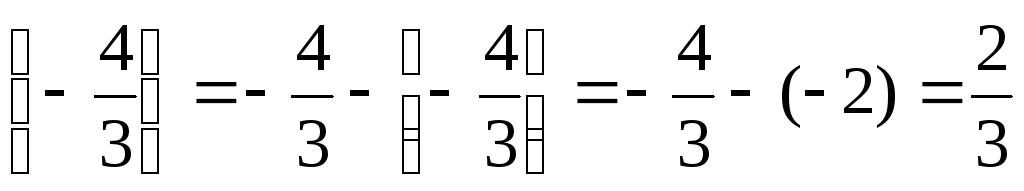
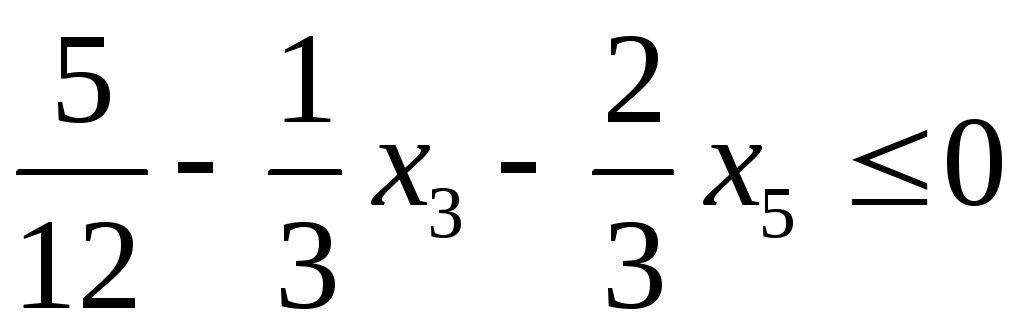
Полученное оптимальное решение расширенной задачи содержит нецелое значение переменной х1, поэтому находим для этой строки дробные части всех нецелых чисел, а именно: и новое неравенство Гомори имеет вид: Выравниваем неравенство Гомори с помощью новой вспомогательной переменной х6, переносим свободный член уравнения в правую часть и получаем новое ограничение: . Добавляем его к решаемой задаче, выравниваем с помощью вспомогательной переменной и решаем расширенную задачу

Б СБ В С1=5 С2=11 С3=0 С4=0 С5=0 С6=0
а1 а2 а3 а4 а5 а6
а2 110 1 0 1 0 0 1 0
а4 0 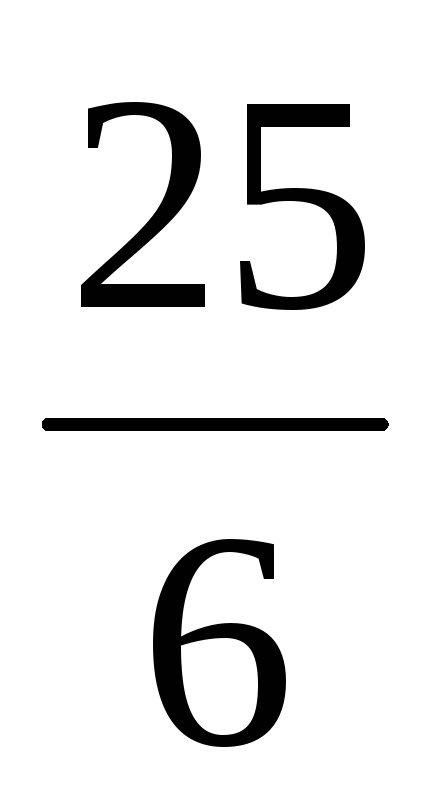0 0 1 0
а1 0 1 0 0 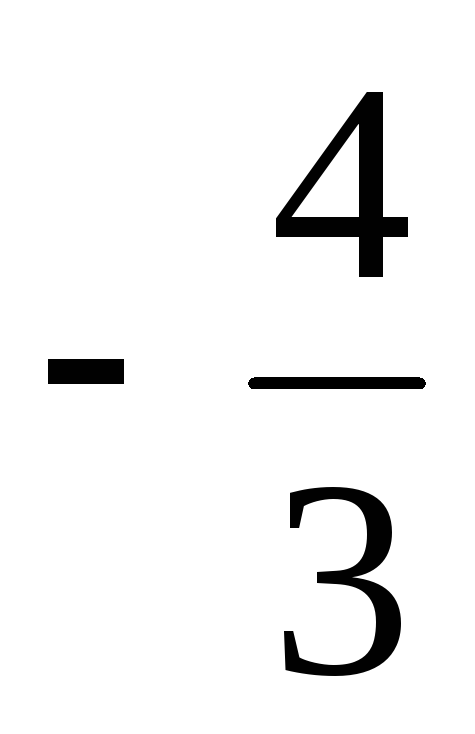0
а6 0 0 0 0 1
∆j =Zj–Сj 0 0 0 0
Б СБ В С1=5 С2=11 С3=0 С4=0 С5=0 С6=0
а1 а2 а3 а4 а5 а6
а2 110 1 0 1 0 0 1 0
а4 0 5 0 0 0 1 -1 -2
а1 0 0 1 0 0 0 -2 1
а3 0 0 0 1 0 2 -3
∆j =Zj–Сj 11 0 0 0 0 1 5

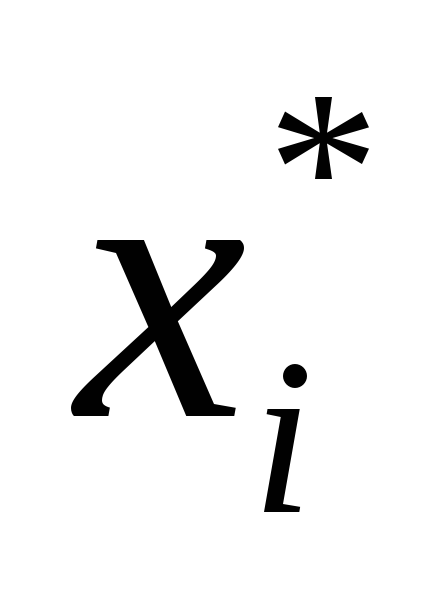
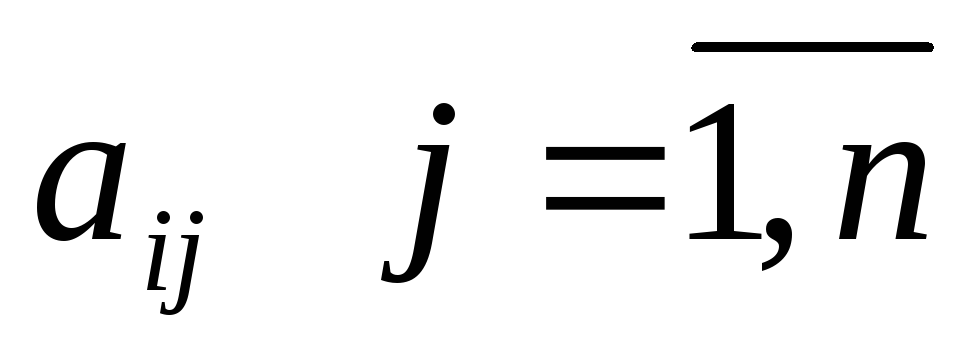
Таким образом, найдено оптимальное решение задачи целочисленного программирования: Zmax =11 при . Замечания: Если в процессе решения в симплексной таблице появится уравнение с нецелой компонентой и целыми коэффициентами в соответствующей строке системы ограничений, то данная задача не имеет целочисленного решения.

Источник

7. Постановка задачи целочисленного программирования (зцлп). Метод Гомори.

Разложенные задачи полностью целочисленные, в которых условие целочисленности распространяются на все переменные и частично целочисленны, в целочисленности налагается только на часть переменных.

Если в (2) среди и есть дробные числа, то каждое уравнение или неравенство с дробными коэффициентами может привести к общему знаменателю и затем обе части умножить на этот общий знаменатель, поэтому не нарушив общности рассуждений, можно предполагать, что коэффициенты целочислены.

Решение целочисленных и непрерывных задач оптимизации имеет принципиальные различия, суть которого заключается в следующем: непрерывные задачи обычно решаются симплекс-методом с построением симплекс-таблиц.

Известно, что для ЗЛП экстремум достигается в крайней точке выпуклого множества или в точке, в которой является выпуклой линейной комбинацией крайних точек. Для ЗЦЛП точкой оптимума может быть любая точка области допустимых решений, поэтому невозможно заменить дискретную задачу непрерывным аналогом, и найдя соответствующее решение и округлить его значение до ближайших целых значений.

Пусть целая часть числа x – [x], огромная – , тогда Если даже оптимальный непрерывной задачи, округлённой до целых значений компонент окажется допустимым, то целевая функция может вести себя так, что её значение будет на нём значительно хуже, чем на оптимальном плане целочисленной задачи.

Перечисленные проблемы предопределяли необходимость разработки специальных методов решения ЗЦЛП, ибо методы последовательного улучшения приводит к целочисленному решению лишь для немногих задач. Методы ЦЛП можно разделить на 3 основные группы:

Сущность 1 состоит в том, что сначала задача решается без условия целочисленности. Если полученный план будет целочисленным, то задача решена. Решение обладает следующими свойствами:

  1. Оно должно быть линейным.
  2. Должно отсекать найденный оптимальный нецелочисленный план.
  3. Не должно отсекать ни одного целочисленного плана.

Дополнительные ограничения, обладающие указанными свойствами, называются правильным отсечением. Затем полученные оптимизационные задачи решаются с учётом нового ограничения. После этого в случае необходимости добавляется новое ограничение.

Геометрическое добавление каждого линейного ограничения отвечает проведению плоскости (гиперплоскости), которая отсекает от многоугольника (многогранника) некоторую его часть вместе с оптимальной точкой с нецелевыми координатами, но не затрагивая ни одной из целочисленных точек этого многоугольника.

Основная идея метода отсекающих плоскостей состоит в том, что на каждом шаге рассматривается задача с ослабленными ограничениями без требования целочисленности, для которой по специальному алгоритму строится некоторое дополнительное ограничение, отсекающее только некоторые нецелочисленные точки. Если полученный в результате оптимальный план содержит только целые компоненты, то автоматически получается соответст. решению ЗЦЛП. В противном случае к системе ограничений задачи должно быть добавлено такое ограничение, для которого:

  1. Найденный нецелочисленный оптимальный план не удовлетворяет вновь добавленному ограничению;
  2. Любой допустимый целочисленный план непрерывной задачи 1-4 удовлетворяет вновь добавленному ограничению.

Приведём обобщённую схему алгоритма Гомори. Структурно он делится на, т. н., большие итерации, каждая из которых содержит этапы:

1. Решение текущей задачи 1, 2 отбросит условия неотрицательности 3 симплекс-методом (малая итерация). Пусть решение исходной задачи с ослабленными ограничениями дало на последнем шаге, соответствующему оптимальному решению, следующие выражения, основных переменных через свободные переменные Кратко это записывается в виде:

Как следует из теории симплекс-метода оптимальным решением задачи в этом случае является вектор

2. Если все компоненты оптимального плана, полученного на первой итерации в целом, то он является оптимальным и для ЗЦЛП 1-4. Если задача ЛП 1-3 не разрешима, то и ЗЦЛП 1-4 также не разрешима. Если среди компонентов оптимального плана есть не целая, то перейдём к следующему этапу.

3. Среди базисных нецелых компонентов оптимального плана следует выбрать компоненту с наибольшей дробной частью.

Пусть компонента не целое число. Рассмотрим уравнение, в котором базисная переменная:

, где R – множество индексов свободных переменных.

Разобьем все коэффициенты и свободные члены уравнения (5) на 2 слагаемых: целую и дробную часть.

Для любого целочисленного решения задачи левая часть (6) – есть целое число, следовательно и правая часть равенства также будет целое число, причём правая часть равенства (6) должна удовлетворяет неравенству:

Это будет сечение Гомори. Т. о., третья итерация состоит в построении для нецелевой базисной компоненты условия отсечения.

4. Неравенство (7) выделением дополнительной неотрицательной целочисленной переменной преобразуется в уравнение и присоединяется к ранее решённой задаче (включить его в симплекс-таблицу с нецелочисленным оптимальным планом). Формируется новая текущая задача. Переход на начало следующей большой итерации.

5. Полученная расширенная ЗЛП решается симплекс-методом. Если полученный оптимальный план будет целочисленным, то ЗЦЛП 1-4 решена. В противном случае следует вернуться к пункту алгоритма 3. Если задача разрешима в целых числах, то после конечного числа итерации оптимальный целочисленный план будет найден.

  • Если в процессе решения появится строка с нецелым свободным членом и целыми остальными коэффициентами, то соответствующее уравнение не имеет решения в целых числах. В таком случае и данная задача не имеет целочисленного оптимального плана.
  • Если число с наибольшей дробной частью окажется несколько то из них выбирается первое по коэффициенту.
  • Несмотря на точность, методы отсечения имеют весьма ограниченную применимость, с их помощью нельзя решить задачи большой размерности.
  • При практической реализации метода Гомори на ЭВМ следует считаться с ошибками округления.

8. Пример решения ЗЦЛП методом Гомори.

Находим общее решение системы:

Выразим целевую функцию через свободные переменные x1 и x3:

Полученный стандартный вид ЦФ применим для решения задач симплекс-методом.

Итерация 1. Используя обычный симплекс-алгоритм решаем непрерывный аналог исходной задачи в котором игнорируются условия целочисленности.

Источник

Оцените статью
© 2024 Программирование