Сумма ряда python math

Вычисление суммы ряды с определенной точностью

Задание звучит так: Даны действительные числа x, ε (x≠0, ε>0) и целое число n. Вычислить с точностью ε:
Я не совсем понимаю, что от меня требуется, поэтому прошу проверить, правильно я все понял и написал код:
(этот код был совсем плох)
Добавлено через 1 час 26 минут
Написал прогу лучше, но не уверен, что правильно
Проверьте, пожалуйста, ее правильность

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

import math x=float(input('x=',)) e=float(input('e=',)) k=1 s=math.sqrt(math.fabs(x)) #первый член ряда if x!=0 and e>0 and math.fabs(s)>=e: while math.fabs(s)>e: a=math.sqrt(math.fabs(x))/k**3 #сам ряд k+=1 s+=a print('summa =', s) else: if math.fabs(s)e: print('s=0') else: print('ne bivaet') input()

Вычисление ряда e^x с определенной точностью
1 Вычисление ex. Вычисление ряда 1 + x + x^/2! + x^3/3! + … для заданного аргумента x с заданной.

Вычисление числа пи с определённой точностью
Возникла проблема с вычисление числа пи. Сразу скажу, что math.pi не подходит, так как нужно больше.

Вычисление функции с определенной точностью
Как вычислить с опред. точность функцию такого вида: \frac? f1 и f2 — тригонометрические.

Green_Caps, вообще не помню когда в последний раз видел, чтобы ТС написал формулу по-человечески, используя форумный редактор! Респект!

Источник

Сумма ряда python math

Last updated: Feb 19, 2023
Reading time · 4 min

# Table of Contents

# Sum all numbers in a range in Python

To sum all numbers in a range:

1. Use the range() class to get a range of numbers.
2. Pass the range object to the sum() function.
3. The sum() function will return the sum of the integers in the range.

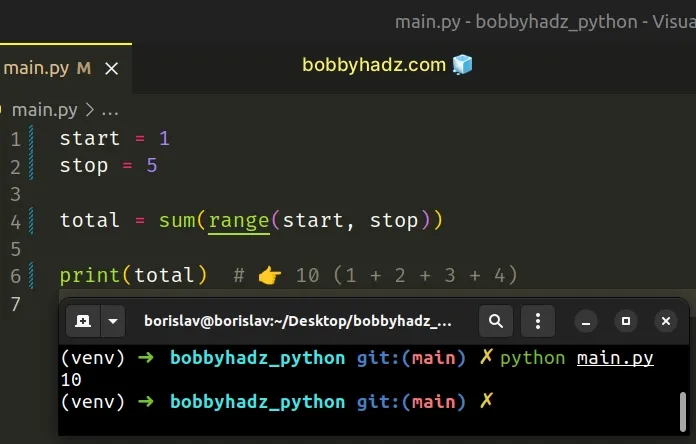
Copied! 
start = 1 stop = 5 total = sum(range(start, stop)) print(total) # 👉️ 10 (1 + 2 + 3 + 4) 

We used the range() class to get a range of numbers.

The range class is commonly used for looping a specific number of times in for loops and takes the following arguments:

Name	Description
start	An integer representing the start of the range (defaults to 0 )
stop	Go up to, but not including the provided integer
step	Range will consist of every N numbers from start to stop (defaults to 1 )

If you only pass a single argument to the range() constructor, it is considered to be the value for the stop parameter.

Copied! 
# 👇️ [0, 1, 2, 3, 4] print(list(range(5))) total = sum(range(5)) print(total) # 👉️ 10 

The example shows that if the start argument is omitted, it defaults to 0 and if the step argument is omitted, it defaults to 1 .

If values for the start and stop parameters are provided, the start value is inclusive, whereas the stop value is exclusive.

Copied! 
# 👇️ [1, 2, 3, 4] print(list(range(1, 5))) total = sum(range(1, 5)) print(total) # 👉️ 10 

If the value for the stop parameter is lower than the value for the start parameter, the range will be empty.

Copied! 
# 👇️ [] print(list(range(5, 1))) total = sum(range(5, 1)) print(total) # 👉️ 0 

The sum function can be used to calculate the sum of the numbers in the range.

The sum function takes an iterable, sums its items from left to right and returns the total.

The sum function takes the following 2 arguments:

Name	Description
iterable	the iterable whose items to sum
start	sums the start value and the items of the iterable. sum defaults to 0 (optional)

# Sum the numbers in a range with a step in Python

If you need to get a range with a step, pass a value for the third argument of the range() class.

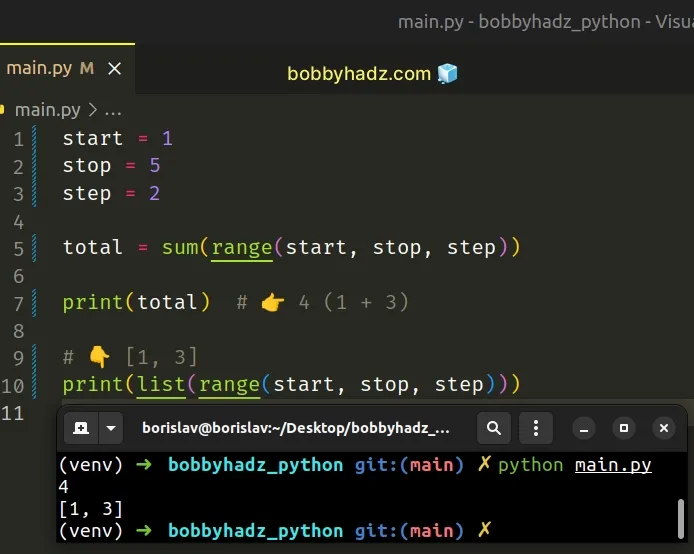
Copied! 
start = 1 stop = 5 step = 2 total = sum(range(start, stop, step)) print(total) # 👉️ 4 (1 + 3) # 👇️ [1, 3] print(list(range(start, stop, step))) 

When the step argument is provided, the range will consist of every N numbers from start to stop .

The value for the step argument defaults to 1 .

# Creating a reusable function

If you have to do this often, define a reusable function.

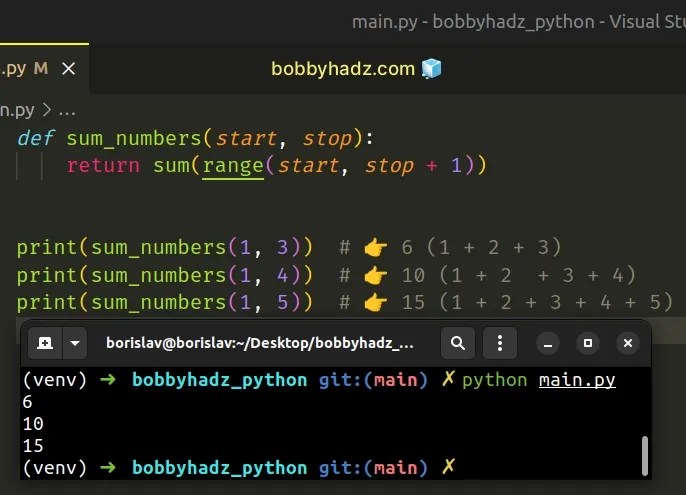
Copied! 
def sum_numbers(start, stop): return sum(range(start, stop + 1)) print(sum_numbers(1, 3)) # 👉️ 6 (1 + 2 + 3) print(sum_numbers(1, 4)) # 👉️ 10 (1 + 2 + 3 + 4) print(sum_numbers(1, 5)) # 👉️ 15 (1 + 2 + 3 + 4 + 5) 

The function takes start and stop values and sums the numbers from start to stop .

Notice that we added 1 to the stop value to make the range inclusive.

If you want to exclude the last number from the range, remove the addition operator.

Copied! 
def sum_numbers(start, stop): return sum(range(start, stop)) print(sum_numbers(1, 3)) # 👉️ 3 (1 + 2) print(sum_numbers(1, 4)) # 👉️ 6 (1 + 2 + 3) print(sum_numbers(1, 5)) # 👉️ 10 (1 + 2 + 3 + 4) 

# Sum the Integers from 1 to N in Python

Multiply by n + 1 and floor-divide by 2 to get the integers from 1 to N.

The result will be the sum of the integers from 1 to N (including N).

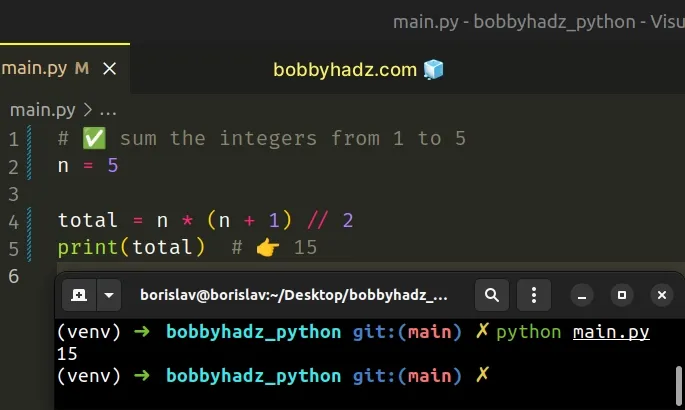
Copied! 
# ✅ sum the integers from 1 to 5 n = 5 total = n * (n + 1) // 2 print(total) # 👉️ 15 

The example multiplies n by n + 1 and floor-divides by 2 to get the sum of the integers from 1 to n .

The result of using the floor division operator is that of a mathematical division with the floor() function applied to the result.

Here is an example that sums the integers from 1 to 100.

Copied! 
n = 100 total = n * (n + 1) // 2 print(total) # 👉️ 5050 

All we had to do is update the value of n to get the sum of the integers from 1 to 100 .

If you don’t want to use a formula, use the range() class from the previous subheading.

# Sum the numbers in a range that are divisible by N

If you need to sum the numbers in a range that are divisible by N, use a while loop.

Copied! 
def sum_divisible_in_range(start, stop, divisor): while start % divisor != 0: start += 1 return sum(range(start, stop, divisor)) print(sum_divisible_in_range(1, 6, 2)) # 👉️ 6 print(sum_divisible_in_range(1, 7, 3)) # 👉️ 9 print(sum_divisible_in_range(1, 8, 4)) # 👉️ 4 

we used a while loop to iterate until the start value reaches the divisor .

The last step is to create a range with the start , stop and divisor values and sum them.

# Additional Resources

You can learn more about the related topics by checking out the following tutorials:

I wrote a book in which I share everything I know about how to become a better, more efficient programmer.

Источник

Python-сообщество

• Начало
• » Python для новичков
• » вычисление суммы ряда e ^(x) с заданной точностью

#1 Янв. 12, 2020 17:07:16

вычисление суммы ряда e ^(x) с заданной точностью

Камрады, need help:
Задача — с заданой точностью ε, (0<ε<1), найти е^х=1+x/1!+x^2/2!+…+x^n/n!
проверить значение

#2 Янв. 13, 2020 02:07:24

вычисление суммы ряда e ^(x) с заданной точностью

Надо эту задачу делать через рекуррентные соотношения (то есть функция факториала не используется).

Надо формулу n-ого члена ряда поделить на формулу (n-1)-ого члена ряда. Это даст коэффициент, на который умножается каждый член ряда, чтобы получить следующий член ряда. Потом, начиная с первого члена ряда, нужно умножать член ряда на этот коэффициент; будет получаться следующий член ряда, который нужно прибавлять к частичной сумме. Таким образом, когда частичная сумма сойдётся к одному числу в пределах заданной точности (то есть при добавлении новых членов ряда частичная сумма в пределах заданной точности не будет меняться), можно прекратить вычисление.

#!/usr/bin/env python3 # вычисляет сумму ряда e ^ (-x) с заданной точностью # # e ^ (-x) = 1 - x + (x ^ 2) / 2! - (x ^ 3) / 3! + # + . + (-1 ^ n) * (x ^ n) / n! import math def emx(x, eps): s, sl, psl, i = 0, 1, 0, 1 while abs(sl - psl) > eps: s += sl psl = sl sl *= -x / i i += 1 return s if __name__ == '__main__': print(math.exp(-4)) for e in ( 1, 0.1, 0.01, 0.001, 0.0001, 0.00001, 0.000001, 0.0000001, ): x = 4 print('<> eps=<>'.format(emx(x, e), e)) 

Отредактировано py.user.next (Янв. 17, 2020 01:02:52)

#3 Янв. 13, 2020 12:15:33

вычисление суммы ряда e ^(x) с заданной точностью

py.user.next
Надо эту задачу делать через рекуррентные соотношения (то есть функция факториала не используется).Надо формулу n-ого члена ряда поделить на формулу (n-1)-ого члена ряда. Это даст коэффициент, на который умножается каждый член ряда, чтобы получить следующий член ряда. Потом, начиная с первого члена ряда, нужно умножать член ряда на этот коэффициент; будет получаться следующий член ряда, который нужно прибавлять к частичной сумме. Таким образом, когда частичная сумма сойдётся к одному числу в пределах заданной точности (то есть при добавлении новых членов ряда частичная сумма в пределах заданной точности не будет меняться), можно прекратить вычисление.Для e^(-x) делал:

import math def emx(x, eps): s, s1, i = 0, 1, 1 while abs(s1 + (math.pow(x, i) / math.factorial(i))) > eps: s = s + s1 s1 = (math.pow(x, i) / math.factorial(i)) i = i + 1 return s print(emx(4, 0.01)) print(math.exp(4)) estimated_error = (math.exp(4))-(emx(4, 0.01)) print(estimated_error) 

Отредактировано FishHook (Янв. 13, 2020 12:34:13)

#4 Янв. 13, 2020 13:08:05

вычисление суммы ряда e ^(x) с заданной точностью

s1 = (math.pow(x, i) / math.factorial(i)) 

Факториал не используется, написал же. Использование факториала в таких задачах — это ошибка.
Делай без факториала, забудь про math.factorial().
Вообще забудь про модуль math, в учебных задачах надо функции модуля math писать самому.

Отредактировано py.user.next (Янв. 13, 2020 13:11:29)

#5 Янв. 17, 2020 00:58:44

вычисление суммы ряда e ^(x) с заданной точностью

#!/usr/bin/env python3 # вычисляет сумму ряда e ^ x с заданной точностью # # е ^ х = 1 + x / 1! + (x ^ 2) / 2! + . + (x ^ n) / n! # import math def ex(x, eps): s, sl, psl, i = 0, 1, 0, 1 while abs(sl - psl) >= eps or x + 1 == i: s += sl psl = sl sl *= x / i i += 1 return s if __name__ == '__main__': print(math.exp(4)) for e in ( 1, 0.1, 0.01, 0.001, 0.0001, 0.00001, 0.000001, 0.0000001, ): x = 4 print('<> eps=<>'.format(ex(x, e), e)) 

[guest@localhost py]$ ./row_ex.py 
54.598150033144236
53.43174603174603 eps=1
54.54818021484688 eps=0.1
54.59398264287153 eps=0.01
54.5978829056501 eps=0.001
54.598136483106295 eps=0.0001
54.598147216543595 eps=1e-05
54.598149928148814 eps=1e-06
54.59815001423152 eps=1e-07
[guest@localhost py]$

Отредактировано py.user.next (Янв. 17, 2020 01:02:38)

Источник