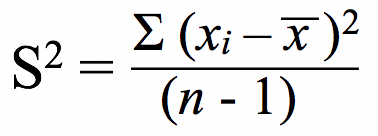Std of list python

Standard deviation of a list

Now I want to take the mean and std of *_Rank[0] , the mean and std of *_Rank[1] , etc.
(ie: mean and std of the 1st digit from all the (A..Z)_rank lists;
the mean and std of the 2nd digit from all the (A..Z)_rank lists;
the mean and std of the 3rd digit. ; etc).

8 Answers 8

Since Python 3.4 / PEP450 there is a statistics module in the standard library, which has a method stdev for calculating the standard deviation of iterables like yours:

>>> A_rank = [0.8, 0.4, 1.2, 3.7, 2.6, 5.8] >>> import statistics >>> statistics.stdev(A_rank) 2.0634114147853952 

It’s worth pointing out that pstddev should probably be used instead if your list represents the entire population (i.e. the list is not a sample of a population). stddev is calculated using sample variance and will overestimate the population mean.

The functions are actually called stdev and pstdev , not using std for standard as one would expect. I couldn’t edit the post as edits need to modify at least 6 chars.

I would put A_Rank et al into a 2D NumPy array, and then use numpy.mean() and numpy.std() to compute the means and the standard deviations:

In [17]: import numpy In [18]: arr = numpy.array([A_rank, B_rank, C_rank]) In [20]: numpy.mean(arr, axis=0) Out[20]: array([ 0.7 , 2.2 , 1.8 , 2.13333333, 3.36666667, 5.1 ]) In [21]: numpy.std(arr, axis=0) Out[21]: array([ 0.45460606, 1.29614814, 1.37355985, 1.50628314, 1.15566239, 1.2083046 ]) 

the result of numpy.std is not correct. Given these values: 20,31,50,69,80 and put in Excel using STDEV.S(A1:A5) the result is 25,109 NOT 22,45.

@JimClermonts It has nothing to do with correctness. Whether or not ddof=0 (default, interprete data as population) or ddof=1 (interprete it as samples, i.e. estimate true variance) depends on what you’re doing.

To further clarify @runDOSrun’s point, the Excel function STDEV.P() and the Numpy function std(ddof=0) calculate the population sd, or uncorrected sample sd, whilst the Excel function STDEV.S() and Numpy function std(ddof=1) calculate the (corrected) sample sd, which equals sqrt(N/(N-1)) times the population sd, where N is the number of points. See more: en.m.wikipedia.org/wiki/…

Here’s some pure-Python code you can use to calculate the mean and standard deviation.

All code below is based on the statistics module in Python 3.4+.

def mean(data): """Return the sample arithmetic mean of data.""" n = len(data) if n < 1: raise ValueError('mean requires at least one data point') return sum(data)/n # in Python 2 use sum(data)/float(n) def _ss(data): """Return sum of square deviations of sequence data.""" c = mean(data) ss = sum((x-c)**2 for x in data) return ss def stddev(data, ddof=0): """Calculates the population standard deviation by default; specify ddof=1 to compute the sample standard deviation.""" n = len(data) if n < 2: raise ValueError('variance requires at least two data points') ss = _ss(data) pvar = ss/(n-ddof) return pvar**0.5 

Note: for improved accuracy when summing floats, the statistics module uses a custom function _sum rather than the built-in sum which I've used in its place.

>>> mean([1, 2, 3]) 2.0 >>> stddev([1, 2, 3]) # population standard deviation 0.816496580927726 >>> stddev([1, 2, 3], ddof=1) # sample standard deviation 0.1 

@Ranjith: if you want to calculate the sample variance (or sample SD) you can use n-1 . The code above is for the population SD (so there are n degrees of freedom).

Hello Alex, Could you please post function for calculating sample standard deviation? I am limited with Python2.6, so I have to relay on this function.

@VenuS: Hello, I've edited the stddev function so that it can calculate both sample and population standard deviations.

In Python 2.7.1, you may calculate standard deviation using numpy.std() for:

• Population std: Just use numpy.std() with no additional arguments besides to your data list.
• Sample std: You need to pass ddof (i.e. Delta Degrees of Freedom) set to 1, as in the following example:

numpy.std(< your-list >, ddof=1)

The divisor used in calculations is N - ddof, where N represents the number of elements. By default ddof is zero.

It calculates sample std rather than population std.

Using python, here are few methods:

import statistics as st n = int(input()) data = list(map(int, input().split())) 

Approach1 - using a function

Approach2: calculate variance and take square root of it

variance = st.pvariance(data) devia = math.sqrt(variance) 

Approach3: using basic math

mean = sum(data)/n variance = sum([((x - mean) ** 2) for x in X]) / n stddev = variance ** 0.5 print("".format(stddev)) 

Note:

• variance calculates variance of sample population
• pvariance calculates variance of entire population
• similar differences between stdev and pstdev

In python 2.7 you can use NumPy's numpy.std() gives the population standard deviation.

In Python 3.4 statistics.stdev() returns the sample standard deviation. The pstdv() function is the same as numpy.std() .

The statistics module accepts int , float , Decimal and Fraction -- Decimal in particular could be useful if you need exact or want to alter the precision.

from math import sqrt def stddev(lst): mean = float(sum(lst)) / len(lst) return sqrt(float(reduce(lambda x, y: x + y, map(lambda x: (x - mean) ** 2, lst))) / len(lst)) 

There's nothing 'pure' about that 1-liner. Yuck. Here's more pythonic version: sqrt(sum((x - mean)**2 for x in lst) / len(lst))

The other answers cover how to do std dev in python sufficiently, but no one explains how to do the bizarre traversal you've described.

I'm going to assume A-Z is the entire population. If not see Ome's answer on how to inference from a sample.

So to get the standard deviation/mean of the first digit of every list you would need something like this:

#standard deviation numpy.std([A_rank[0], B_rank[0], C_rank[0], . Z_rank[0]]) #mean numpy.mean([A_rank[0], B_rank[0], C_rank[0], . Z_rank[0]]) 

To shorten the code and generalize this to any nth digit use the following function I generated for you:

def getAllNthRanks(n): return [A_rank[n], B_rank[n], C_rank[n], D_rank[n], E_rank[n], F_rank[n], G_rank[n], H_rank[n], I_rank[n], J_rank[n], K_rank[n], L_rank[n], M_rank[n], N_rank[n], O_rank[n], P_rank[n], Q_rank[n], R_rank[n], S_rank[n], T_rank[n], U_rank[n], V_rank[n], W_rank[n], X_rank[n], Y_rank[n], Z_rank[n]] 

Now you can simply get the stdd and mean of all the nth places from A-Z like this:

#standard deviation numpy.std(getAllNthRanks(n)) #mean numpy.mean(getAllNthRanks(n)) 

Источник

Как рассчитать стандартное отклонение списка в Python

Вы можете использовать один из следующих трех методов для вычисления стандартного отклонения списка в Python:

Способ 1: использовать библиотеку NumPy

import numpy as np #calculate standard deviation of list np.std( my_list ) 

Способ 2: использовать библиотеку статистики

import statistics as stat #calculate standard deviation of list stat. stdev ( my_list ) 

Способ 3: использовать пользовательскую формулу

#calculate standard deviation of list st. stdev ( my_list ) 

В следующих примерах показано, как использовать каждый из этих методов на практике.

Метод 1: рассчитать стандартное отклонение с помощью библиотеки NumPy

В следующем коде показано, как рассчитать как стандартное отклонение выборки, так и стандартное отклонение совокупности списка с помощью NumPy:

import numpy as np #define list my_list = [3, 5, 5, 6, 7, 8, 13, 14, 14, 17, 18] #calculate sample standard deviation of list np.std( my_list, ddof= 1 ) 5.310367218940701 #calculate population standard deviation of list np.std( my_list ) 5.063236478416116 

Обратите внимание, что стандартное отклонение совокупности всегда будет меньше, чем стандартное отклонение выборки для данного набора данных.

Метод 2: расчет стандартного отклонения с использованием библиотеки статистики

В следующем коде показано, как рассчитать как стандартное отклонение выборки, так и стандартное отклонение генеральной совокупности для списка с помощью библиотеки статистики Python:

import statistics as stat #define list my_list = [3, 5, 5, 6, 7, 8, 13, 14, 14, 17, 18] #calculate sample standard deviation of list stat. stdev (my_list) 5.310367218940701 #calculate population standard deviation of list stat. pstdev (my_list) 5.063236478416116 

Метод 3: расчет стандартного отклонения с использованием пользовательской формулы

В следующем коде показано, как вычислить как стандартное отклонение выборки, так и стандартное отклонение совокупности списка без импорта каких-либо библиотек Python:

#define list my_list = [3, 5, 5, 6, 7, 8, 13, 14, 14, 17, 18] #calculate sample standard deviation of list (sum((x-(sum(my_list) / len(my_list))) \*\* 2 for x in my_list) / (len(my_list)-1)) \*\* 0.5 5.310367218940701 #calculate population standard deviation of list (sum((x-(sum(my_list) / len(my_list))) \*\* 2 for x in my_list) / len(my_list)) \*\* 0.5 5.063236478416116 

Обратите внимание, что все три метода рассчитали одни и те же значения для стандартного отклонения списка.

Источник

Python calculate standard deviation of list

Standard Deviation
Standard deviation means the variation or dispersion of values of a data set from its mean or average. For a list, it means the variation of its elements from the mean value of elements.
Python provides different ways to calculate standard deviation and we can also calculate it by applying its formula. All this will be covered in this article.
Method 1 : Using stdev()
Python statistics module has a stdev() function which takes a data set as argument and returns square root of variance, also called standard deviation. Example,

import statistics # create list l=[1,2,3,4,5] d=statistics.stdev(l) print('Standard deviation =',d)

Standard deviation = 1.5811388300841898

This method is available since Python 3.4
Method 2 : Using pstdev()
Python statistics module has a pstdev() function which calculates standard deviation over the entire population or data set. Example,

import statistics l=[1,2,3,4,5] print('Standard deviation =',statistics.pstdev(l))

Standard deviation = 1.4142135623730951

stdev() takes into account sample data[(n -1 ) elements] to calculate variance. Hence, there is a difference between the results of stdev() and pstddev() .
Since stdev() takes a smaller data set, its value is higher as compared to pstdev() .

Method 3 : Using numpy library
Python’s numpy (shorthand for Numerical Python) library contains mathematical functions to work on large data sets. It has a function std() which takes a data set argument and returns its standard deviation. Example,

import numpy as n l=[1,2,3,4,5] print('Standard deviation =',n.std(l))

Standard deviation = 1.4142135623730951

There is a difference in the values returnd from statistics module and numpy because statistics considers (n-1) elements while numpy takes into account n elements.

Notice that the result of numpy and pstdev() are identical, since they both cover all list elements.
Method 4 : Using formula
Mathematically, standard deviation is the square root of variance. Variance is calculated using below formula

where,
x_i is value of obervation or a single list element,
x̄ is the average or mean of list elements,
n is the total number of list elements,
S 2 is the variance, and
Σ is the summation.

So, if you carefully look at the formula, it is subtracting each list element from the list average, squaring the result, adding them up and dividing by the list element count.
This values will be variance. Finally, take the square root of variance to get standard deviation.
We can apply this formula in a python program to calculate standard deviation of list elements. Example,

l=[1,2,3,4,5] # calculate average of list mean = sum(l) / len(l) # apply formula variance = sum((x - mean)**2 for x in l) / len(l) # square root of variance std_dev = variance ** 0.5 print('Standard deviation =',std_dev)

To calculate mean or average, Python’s inbuilt sum() and len() functions are used.

To calculate, variance, we are iterating over a list, subtracting the mean from each element and taking its square. All these operations are performed in below line

This syntax is called Python list comprehension .
If you are not familiar with this syntax, then replace it with Python for loop as shown below.

element_sum = 0 for x in l: element_sum += (x-mean)**2 variance = element_sum / len(l)

Divide the sum of elements with the length of list to get variance. Finally, calculate standard deviation by taking square root of varianceby raising it to the power of 0.5.
Output of this code is

Standard deviation = 1.4142135623730951

Note that this method does not require any external library or module, it is a pure mathematical solution.

That is all on different methods to calculate standard deviation in Python. Hope the article was useful.

Источник