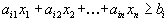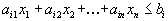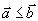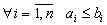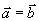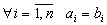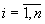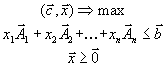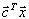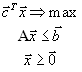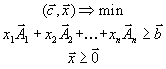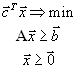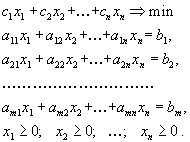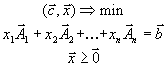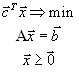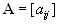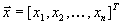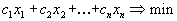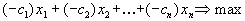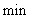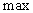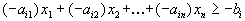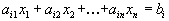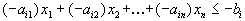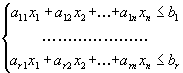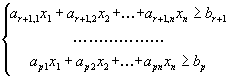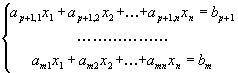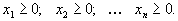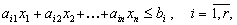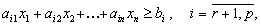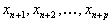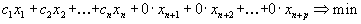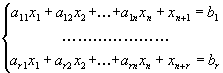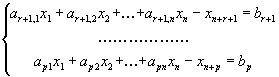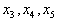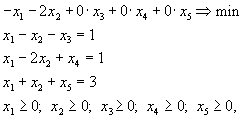Стандартная форма представления задач линейного программирования

Стандартная форма задачи линейного программирования

Рассмотрим подробнее стандартную и каноническую форму задач линейного программирования. В стандартной форме все ограничения являются неравенствами, а в канонической — равенствами (за исключением ограничений, требующих чтобы все ограничения были неотрицательны), но есть определенные нюансы.

Стандартная форма

В стандартной форме задаются \( n \) действительных чисел \(с_1, c_2, \ldots, c_n \); \( m \) действительных чисел \( b_1,b_2,\ldots ,b_m \); и \( mn \) действительных чисел \( a_ \), где \( i=1,2, \ldots, m \) и \( j = 1,2, \ldots, n \).
Требуется найти \( n \) действительных чисел \( x_1,x_2,\ldots,x_n \) которые:

Максимизируют целевую функцию \( \sum\limits_^n c_j x_j \) при заданных ограничениях : \( \sum\limits_^n a_ x_j \le b_i\) при \( i=1,2, \ldots, m \) и ограничениях неотрицательности \( x_j \ge 0 \) при \( j= 1,2,\ldots,n \)

Преобразование в стандартную форму

Задача находится не в стандартной форме если:

1. Целевая функция минимизируется, а не максимизируется
2. На имеющиеся переменные не наложены условия неотрицательности
3. Некоторые ограничения имеют форму равенства, т.е. имеют знак равенства вместо меньше или равно
4. Некоторые ограничения вместо знака «меньше или равно» имеют знак «больше или равно».

Как получить стандартную форму в таких случаях? Рассмотрим по пунктам:

1. Достаточно поменять знаки целевой функции, например: \( -5x_1+2x_2 \to min \) эквивалентно \( 5x_1-2x_2 \to max \).
2. Если отсутствует ограничение неотрицательности для переменной \(x_j\), то заменяем эту переменную выражением \( x_j^-x_j^ \) из двух неотрицательных переменных \(x_j^,x_j^ \ge 0 \).
3. Если ограничение имеет вид равенства, то заменяем его парой из двух неравеств «меньше или равно» и «больше или равно».
4. Для смены смены выда неравенства с «больше или равно» на «меньше или равно» умножаем обе части неравества на -1 и меняем знак сравнения.

Шаг 1. Меняем знак целевой функции

Шаг 2. Для второй переменной \(x_2\) ограничений неотрицательности нет. Заменим на выражение \(x_2=x_2^-x_2^ \):

Шаг 3. Заменяем равенство на два неравенства:

Шаг 4. Изменяем знак неравества:

Получили задачу в стандартном виде.

В данной заметке рассмотрен основной подход к виду стандартной формы задачи ЛП. Существует и другой подход, например в книге Соколов А. В., Токарев В.В. Методы оптимальных решений. В 2-х т. Т 1. Общие положения. математическое программирование. — 3-е изд. — 564 с. на с. 423 выделяется стандартный вид задачи на максимум:

Однако в общепринят первый вариант из которого второй получается простым умножением обеих частей неравенств на -1.

Источник

5. Формы представления задач линейного программирования

1. Стандартная форма на максимум:

1. Стандартная форма на минимум:

1. Каноническая форма представления:

6. Структура допустимого множества и типы решений задач линейного программирования

Каждое функциональное ограничение, входящее в формальную запись задачи линейного программирования, представляет собой некоторые замкнутые полупространства размерности n (при условии ограничения в виде неравенства). Если ограничения заданы в виде равенства, то оно отображается гиперплоскостью в n-мерном пространстве. Прямые ограничения образуют также замкнутые полупространства. Следовательно, допустимое множество задач линейного программирования задается системой ограничений и представляет собой пересечение замкнутых полупространств и/или гиперплоскостей. Такое образование называетсямногогранным множеством. Многогранное множество всегда замкнуто и выпукло, но в частном случае может быть пустым или неограниченным, а размерность его может составлять n или менее. Рассмотрим примеры формирования допустимого множества для n=2, тогда все рассуждения будут рассматриваться на плоскости. Пример 1 Данная система решений не имеет (т.к. нет пересечений), следовательно, Х а =. Пример 2. Данная система имеет решение в точке (3,0), следовательно, Х а =(3,0). Пример 3. Областью допустимых значений Х а в данном случае является отрезок. Пример 4. Областью допустимых значений Х а в данном случае является ограниченная область. Пример 5. Областью допустимых значений Х а в данном случае является неограниченная область.

7. Типы решений

Если считать, что целевая функция задачи линейного программирования имеет вид f(x₁, …, x_n) = c₁x₁ + … + c_nx_n = C, то эта целевая функция представляет собой семейство параллельных гиперплоскостей в n-мерном пространстве. Если требуется максимизировать целевую функцию, то при графической задаче константа С увеличивается, пока гиперплоскость все еще будет пересекать допустимое множество, т.е.: Δf=(c₁, …, c_n) – градиент целевой функции.Если требуется минимизировать целевую функцию, то гиперплоскость надо сдвигать в направлении противоположном градиенту. Возможны следующие случаи:

1. Задача не имеет решений

1. Задача имеет единственное решение

1. Задача имеет единственное решение

1. Задача имеет множество решений

8. Понятие двойственной задачи

Если имеется задача линейного программирования на max: 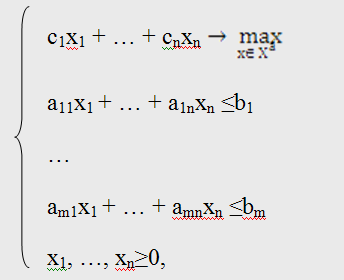то механизм построения двойственной задачи заключается в следующем: это двойственная задача. Связь прямой и двойственной задачи состоит в том, что решение одной из них может быть получено из решения другой. Теоретически доказано, что прямая и двойственная задача либо обе неразрешимы, либо обе имеют решение, причем значения целевых функций для оптимальных решений совпадают. На практике бывают случаи, когда решение двойственной задачи оказывается проще, чем прямой.

9. О методах решения задач линейного программирования

Для задач линейного программирования, особенно для типовых классов таких задач, разработано много специфических методов, причем эти методы часто связаны с решением двойственных задач. Однако, несмотря на специфику различных методов, практически все они реализуют общий метод решения задач линейного программирования, названный симплекс-методом (метод последовательного улучшения оценок). Он был предложен Данцингом в 1947 г. Геометрический метод состоит в следующем: пусть имеется n-переменных х_{1, …,} х_n и p-ограничений, p процесс регуляризации.

Источник

1.2. Стандартная и каноническая формы задачи линейного программирования

Обратите внимание на то, что в указанных выше двух примерах задачи имели достаточно разный вид: в задаче о диете требовалось найти минимум целевой функции, а в задаче о плане производства  максимум. В задаче о диете ограничения имели вид

,

а в задаче о плане производства  вид

.

Такой разнобой неудобен при разработке алгоритмов решения этих задач. Поэтому имеются некоторые стандартные формы задач линейного программирования, к которым и приводят конкретные различные задачи.

Прежде чем выписывать эти формы, договоримся об обозначениях. Для более краткой записи мы будем использовать векторную или матричную запись. Под векторами мы будем понимать вектора-столбцы, например

, ,

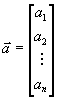
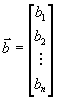
и т.д. Обозначение

будет означать, что

Соответственно, запись

означает, что

Первая стандартная форма задачи линейного программирования имеет вид

; ; ,

,

.

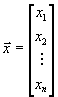
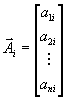
Заметим, что комбинация есть не что иное, как скалярное произведение векторов 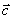и . Поэтому в векторной форме задача (1.7) примет вид

Можно использовать и матричные обозначения. Тогда комбинация

есть произведение

Вторая стандартная форма задачи линейного программирования имеет вид

В векторной форме эта задача имеет вид

и в матричной форме — вид

Канонической формой задачи линейного программирования называется задача вида

В векторной форме эта задача имеет вид

и в матричной форме — вид

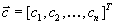
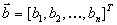
Во всех этих задачах функцию называют целевой функцией. Вектор называют вектором коэффициентов линейной формы, вектор  вектором ограничений.

Матрицу

называют матрицей коэффициентов.

Любой набор чисел , удовлетворяющий ограничениям задачи, называют планом, а множество всех планов  допустимой областью. Тот план, который доставляет экстремум (минимум или максимум) целевой функции, называют оптимальным планом или просто решением задачи линейного программирования.

Правила приведения задач линейного программирования к стандартной и канонической формам

Рассмотрим теперь те приёмы, которые позволяют произвольные формы задач линейного программирования приводить к указанным выше стандартным формам.

1. Превращение мах в min и наоборот.

Если целевая функция в задаче линейного программирования задана в виде

,

то, умножая её на (- 1), приведем её к виду

,

так как смена знака приводит к смене

на .

Аналогично можно заменить

2. Смена знака неравенства.

Если ограничение задано в виде

.

Аналогично, неравенство вида больше либо равно можно превратить в неравенство вида меньше либо равно .

3. Превращение равенства в систему неравенств.

Если ограничение задано в виде

,

то его можно заменить эквивалентной системой двух неравенств

,

или такой же системой неравенств со знаками больше либо равно .

Указанные выше приемы позволяют приводить задачи линейного программирования к стандартной форме.

4. Превращение неравенств в равенства.

Пусть исходная форма задачи линейного программирования имеет вид

Здесь первые r ограничений имеют вид неравенств со знаком меньше либо равно

затем идет группа неравенств со знаком больше либо равно

и, наконец, группа ограничений со знаком = .

Для приведения задачи к канонической форме, где все ограничения имеют вид равенств, вводят дополнительные переменные , которые тоже считаются неотрицательными и записывают исходную задачу в виде

,

т.е. в неравенстве со знаком меньше либо равно добавляют дополнительную неотрицательную переменную, а из неравенства со знаком больше либо равно вычитают дополнительную переменную.

В целевую функцию эти дополнительные переменные включают с коэффициентом 0, т.е. фактически они в целевой функции отсутствуют.

Получив решение задачи (1.17), т.е. решение задачи в канонической форме, для получения решения исходной задачи (1.16) надо просто выбросить из решения значения введенных дополнительных переменных.

Привести к каноническому виду задачу

Введем дополнительные переменные . Переводя мах в min, запишем задачу в виде

что и дает эквивалентную задачу в канонической форме.

Источник

Научная электронная библиотека

Задачами линейного программирования называются оптимизационные задачи, в которых ограничения, представленные в виде равенств или неравенств, и целевая функция линейна. Разработка модели ЛП включает следующие основные этапы: определение переменных задачи, представление её ограничений в виде линейных уравнений или неравенств, задание линейной целевой функции, подлежащей минимизации или максимизации.

Задача ЛП в стандартной форме с m ограничениями и n переменными имеет следующий вид:

максимизировать или минимизировать

Задачи ЛП в стандартной форме можно записать в компактных матричных обозначениях следующим образом:

максимизировать или минимизировать

где A — матрица размерности mxn, x — вектор-столбец размерности nxl, b— вектор-столбец размерности mxl, а c — вектор-строка размерности .1xn.

Обычно A назначается матрицей коэффициентов, x — вектором переменных, b — вектором ресурсов, c — вектором оценок задачи ЛП.

При решении задачи ЛП симплекс-методом требуется, чтобы задача была представлена в стандартной форме. Однако не все практические задачи ее имеют, поэтому для удовлетворения требования алгоритма необходимо следующее.

• 1. При помощи введения дополнительных остаточных или избыточных переменных преобразовать неравенства в равенства.
• 2. Для получения неотрицательных переменных задачи неограниченные по знаку переменные заменить разностью двух неотрицательных.

При решении задач ЛП используются следующие основные понятия. Допустимым решением являются неотрицательные значения переменных, для которых выполняются ограничения, а допустимой областью — совокупность допустимых решений. Оптимальным решением называются такие допустимые значения переменных, при которых ЦФ экстремальна, т.е. имеет оптимальное значение. В ряде случаев, ЦФ имеет одно оптимальное значение при нескольких комбинаций значений переменных, следовательно, задача обладает неединственностью оптимума. Когда в задаче ЛП нет конечного оптимума, то в этом случае существует неограниченный оптимум.

Источник