Стандартная форма модели линейного программирования

Стандартная форма задачи линейного программирования

Рассмотрим подробнее стандартную и каноническую форму задач линейного программирования. В стандартной форме все ограничения являются неравенствами, а в канонической — равенствами (за исключением ограничений, требующих чтобы все ограничения были неотрицательны), но есть определенные нюансы.

Стандартная форма

В стандартной форме задаются \( n \) действительных чисел \(с_1, c_2, \ldots, c_n \); \( m \) действительных чисел \( b_1,b_2,\ldots ,b_m \); и \( mn \) действительных чисел \( a_ \), где \( i=1,2, \ldots, m \) и \( j = 1,2, \ldots, n \).
Требуется найти \( n \) действительных чисел \( x_1,x_2,\ldots,x_n \) которые:

Максимизируют целевую функцию \( \sum\limits_^n c_j x_j \) при заданных ограничениях : \( \sum\limits_^n a_ x_j \le b_i\) при \( i=1,2, \ldots, m \) и ограничениях неотрицательности \( x_j \ge 0 \) при \( j= 1,2,\ldots,n \)

Преобразование в стандартную форму

Задача находится не в стандартной форме если:

1. Целевая функция минимизируется, а не максимизируется
2. На имеющиеся переменные не наложены условия неотрицательности
3. Некоторые ограничения имеют форму равенства, т.е. имеют знак равенства вместо меньше или равно
4. Некоторые ограничения вместо знака «меньше или равно» имеют знак «больше или равно».

Как получить стандартную форму в таких случаях? Рассмотрим по пунктам:

1. Достаточно поменять знаки целевой функции, например: \( -5x_1+2x_2 \to min \) эквивалентно \( 5x_1-2x_2 \to max \).
2. Если отсутствует ограничение неотрицательности для переменной \(x_j\), то заменяем эту переменную выражением \( x_j^-x_j^ \) из двух неотрицательных переменных \(x_j^,x_j^ \ge 0 \).
3. Если ограничение имеет вид равенства, то заменяем его парой из двух неравеств «меньше или равно» и «больше или равно».
4. Для смены смены выда неравенства с «больше или равно» на «меньше или равно» умножаем обе части неравества на -1 и меняем знак сравнения.

Шаг 1. Меняем знак целевой функции

Шаг 2. Для второй переменной \(x_2\) ограничений неотрицательности нет. Заменим на выражение \(x_2=x_2^-x_2^ \):

Шаг 3. Заменяем равенство на два неравенства:

Шаг 4. Изменяем знак неравества:

Получили задачу в стандартном виде.

В данной заметке рассмотрен основной подход к виду стандартной формы задачи ЛП. Существует и другой подход, например в книге Соколов А. В., Токарев В.В. Методы оптимальных решений. В 2-х т. Т 1. Общие положения. математическое программирование. — 3-е изд. — 564 с. на с. 423 выделяется стандартный вид задачи на максимум:

Однако в общепринят первый вариант из которого второй получается простым умножением обеих частей неравенств на -1.

Источник

Научная электронная библиотека

Задачами линейного программирования называются оптимизационные задачи, в которых ограничения, представленные в виде равенств или неравенств, и целевая функция линейна. Разработка модели ЛП включает следующие основные этапы: определение переменных задачи, представление её ограничений в виде линейных уравнений или неравенств, задание линейной целевой функции, подлежащей минимизации или максимизации.

Задача ЛП в стандартной форме с m ограничениями и n переменными имеет следующий вид:

максимизировать или минимизировать

Задачи ЛП в стандартной форме можно записать в компактных матричных обозначениях следующим образом:

максимизировать или минимизировать

где A — матрица размерности mxn, x — вектор-столбец размерности nxl, b— вектор-столбец размерности mxl, а c — вектор-строка размерности .1xn.

Обычно A назначается матрицей коэффициентов, x — вектором переменных, b — вектором ресурсов, c — вектором оценок задачи ЛП.

При решении задачи ЛП симплекс-методом требуется, чтобы задача была представлена в стандартной форме. Однако не все практические задачи ее имеют, поэтому для удовлетворения требования алгоритма необходимо следующее.

• 1. При помощи введения дополнительных остаточных или избыточных переменных преобразовать неравенства в равенства.
• 2. Для получения неотрицательных переменных задачи неограниченные по знаку переменные заменить разностью двух неотрицательных.

При решении задач ЛП используются следующие основные понятия. Допустимым решением являются неотрицательные значения переменных, для которых выполняются ограничения, а допустимой областью — совокупность допустимых решений. Оптимальным решением называются такие допустимые значения переменных, при которых ЦФ экстремальна, т.е. имеет оптимальное значение. В ряде случаев, ЦФ имеет одно оптимальное значение при нескольких комбинаций значений переменных, следовательно, задача обладает неединственностью оптимума. Когда в задаче ЛП нет конечного оптимума, то в этом случае существует неограниченный оптимум.

Источник

1.4.2 Стандартная форма задачи линейного программирования

Задачу с неотрицательными переменными, все остальные ограничения которой имеют форму неравенств одного знака (, если задача на максимум, и, если на минимум), будем называтьстандартной формойзаписи задачи линейного программирования:

или

Любая задача в смешанной форме может быть приведена к любой из стандартных форм. Рассмотрим приведение к стандартной форме на max(наminприводится аналогично).

Если какая-то из переменных задачи не ограничена по своему знаку, то ее заменяют на разность двух неотрицательных переменных точно так же, как это делается при приведении задачи к канонической форме (см. раздел 1.4.1).

Необходимо добиться, чтобы во всех остальных ограничениях стоял знак . Предположим, что в некотором ограничении стоит знак. Тогда обе его части умножаются на -1, при этом знак неравенства меняется на противоположный.

Предположим, что некоторое ограничение является уравнением. Тогда его заменяют на два неравенства следующим образом (в самом деле, ведь «равно» означает «не больше и не меньше»):

Кроме того, если при приведении задачи к канонической форме было не важно, максимизируется или минимизирутся целевая функция, то теперь необходимо добиться определенного направления экстремизации (в данном случае, максимизации). Предположим, что целевая функция задачи минимизируется. Тогда к максимизации переходят, умножив выражение для нее на -1:

Отметим, что задача производственного планирования из раздела 1.1 была с самого начала построена в стандартной форме на максимум.

1.4.3 Матричная форма записи

Если задача линейного программирования приведена к стандартной или канонической форме, ее удобно кратко записать в матричной форме. С этой целью вводятся следующие обозначения:

С = (с₁, с₂, . . ., с_j, . . . , с_n) – вектор-строка коэффициентов целевой функции,

B = — вектор-столбец свободных членов (правых частей ограничений),

X = — вектор-столбец переменных,

A = — матрица коэффициентов в левых частях ограничений (каждая ее строка соответствует ограничению, а каждый столбец – переменной).

Тогда задача линейного программирования в канонической форме запишется следующим образом:

Задача в стандартной форме будет иметь вид:

или .

В самом деле, по правилам перемножения векторов СХ = с₁х₁+ с₂х₂+ … + с_nх_n=. Это и есть линейное выражение в целевой функции.

Умножая матрицу А размерности (mxn) на вектор Х (nx1), получают столбец изmвыражений, т.е. матрицу (mx1). Каждое их этих выражений получают умножением строки матрицы А на столбец Х, т.е. а_i1х₁ + а_i2х₂+ … + а_i1х_n=. Тогда АХ представляет собой столбец выражений в левых частях ограничений: АХ =. Благодаря тому, что во всех ограничениях стоит один и тот же знак, этот столбец можно сравнить со столбцом В. Тогда запись АХ = В представляет собой систему уравнений в ограничениях задачи в канонической форме (АХВ или АХВ – соответственно системы неравенств в задачах в стандартной форме).

Отметим, что О в формулах (10) и (11) представляет собой не одно число, а нулевой вектор (столбец из nнулей), поскольку каждая изnпеременных сравнивается с нулем.

Источник

Линейное программирование

1.1. Примеры моделей, приводящих к задачам линейного программирования

Линейное программирование является одной из основных частей того раздела современной математики, который получил название математического программирования. В общей постановке задачи этого раздела выглядят следующим образом.

Имеются какие-то переменные и функция этих переменных , которая носит название целевой функции. Ставится задача: найти экстремум (максимум или минимум) целевой функции при условии, что переменные x принадлежат некоторой области G:

В зависимости от вида функции и области G и различают разделы математического программирования: квадратичное программирование, выпуклое программирование, целочисленное программирование и т.д. Подробнее об этом будет сказано в заключении.

Линейное программирование характеризуется тем, что

является линейной функцией переменных ;

б) область G определяется системой линейных равенств или неравенств.

Чтобы понять, откуда берутся задачи линейного программирования, рассмотрим некоторые, уже ставшие классическими, примеры подобных задач.

Задача о диете

Задача о диете возникает при составлении наиболее экономного (т.е. наиболее дешевого) рациона питания животных, удовлетворяющего определенным медицинским требованиям.

Предположим, что в нашем распоряжении имеется n продуктов питания (сено, зерно, комбикорм, соль и т.д.). Обозначим эти продукты через

. Предположим, что

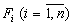
есть стоимость единицы веса (например,

стоимость одного килограмма) продукта .

Рациональная диета должна доставлять животному определенные компоненты (белки, жиры, углеводы, витамины, микроэлементы и т.д.). Обозначим эти компоненты через . Тогда можно составить таблицу — справочник, указывающую, какое количество каждого компонента имеется в единице веса каждого продукта.

Источник