Способы задания графа программирование

Вступление

Как оказалось тема алгоритмов интересна Хабра-сообществу. Поэтому я как и обещал, начну серию обзоров «классических» алгоритмов на графах.
Так как публика на Хабре разная, а тема интересна многим, я должен начать с нулевой части. В этой части я расскажу что такое граф, как он представлен в компьютере и зачем он используется. Заранее прошу прощения у тех кто это все уже прекрасно знает, но для того чтобы объяснять алгоритмы на графах, нужно сначала объяснить что такое граф. Без этого никак.

Основы

В математике, Граф — это абстрактное представление множества объектов и связей между ними. Графом называют пару (V, E) где V это множество вершин, а E множество пар, каждая из которых представляет собой связь (эти пары называют рёбрами).
Граф может быть ориентированным или неориентированным. В ориентированном графе, связи являются направленными (то есть пары в E являются упорядоченными, например пары (a, b) и (b, a) это две разные связи). В свою очередь в неориентированном графе, связи ненаправленные, и поэтому если существует связь (a, b) то значит что существует связь (b, a).

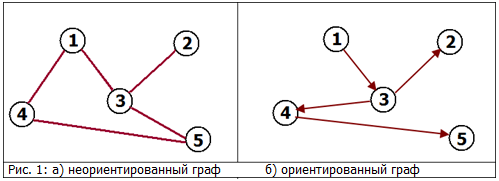
Неориентированный граф: Соседство (в жизни). Если (1) сосед (3), то (3) сосед (1). См рис. 1.а

Ориентированный граф: Ссылки. Сайт (1) может ссылаться на сайт (3), но совсем не обязательно (хотя возможно) что сайт (3) ссылается сайт (1). См рис. 1.б

Степень вершины может быть входящая и исходящая (для неориентированных графов входящая степень равна исходящей).
Входящая степень вершины v это количество ребер вида (i, v), то есть количество ребер которые «входят» в v.
Исходящая степень вершины v это количество ребер вида (v , i), то есть количество ребер которые «выходят» из v.
Это не совсем формальное определение (более формально определение через инцидентность), но оно вполне отражает суть

Путь в графе это конечная последовательность вершин, в которой каждые две вершины идущие подряд соединены ребром. Путь может быть ориентированным или неориентированным в зависимости от графа. На рис 1.а, путем является например последовательность [(1), (4), (5)] на рис 1.б, [(1), (3), (4), (5)].

У графов есть ещё много разных свойств (например они могут быть связными, двудольными, полными), но я не буду описывать все эти свойства сейчас, а в следующих частях когда эти понятия понадобятся нам.

Представление графов

Существует два способа представления графа, в виде списков смежности и в виде матрицы смежности. Оба способа подходят для представления ориентированных и неориентированных графов.

Матрица смежности
Этот способ является удобным для представления плотных графов, в которых количество рёбер (|E|) примерно равно количеству вершин в квадрате (|V| 2 ).
В данном представлении мы заполняем матрицу размером |V| x |V| следущим образом:
A[i][j] = 1 (Если существует ребро из i в j)
A[i][j] = 0 (Иначе)
Данный способ подходит для ориентированных и неориентированных графов. Для неориентированных графов матрица A является симметричной (то есть A[i][j] == A[j][i], т.к. если существует ребро между i и j, то оно является и ребром из i в j, и ребром из j в i). Благодаря этому свойству можно сократить почти в два раза использование памяти, храня элементы только в верхней части матрицы, над главной диагональю)
Понятно что с помощью данного способа представления, можно быстро проверить есть ли ребро между вершинами v и u, просто посмотрев в ячейку A[v][u].
С другой стороны этот способ очень громоздкий, так как требует O (|V| 2 ) памяти для хранения матрицы.

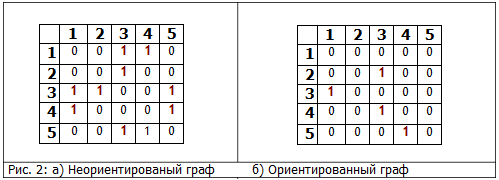
На рис. 2 приведены представления графов из рис. 1 с помощью матриц смежности.

Списки смежности
Данный способ представления больше подходит для разреженных графов, то есть графов у которых количество рёбер гораздо меньше чем количество вершин в квадрате (|E| В данном представлении используется массив Adj содержащий |V| списков. В каждом списке Adj[v] содержатся все вершины u, так что между v и u есть ребро. Память требуемая для представления равна O (|E| + |V|) что является лучшим показателем чем матрица смежности для разреженных графов.
Главный недостаток этого способа представления в том, что нет быстрого способа проверить существует ли ребро (u, v).

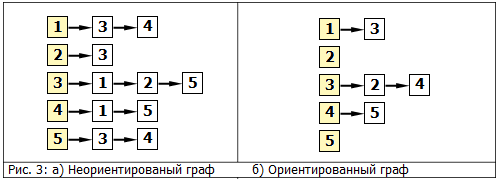
На рис. 3 приведены представления графов из рис. 1 с помощью списков смежности.

Применение

Те кто дочитал до этого места, наверное задали себе вопрос, а где же собственно я смогу применить графы. Как я и обещал я буду стараться приводить примеры. Самый первый пример который приходит в голову это социальная сеть. Вершинами графа являются люди, а ребрами отношения (дружба). Граф может быть неориентированным, то есть я могу дружить только с теми кто дружит со мной. Либо ориентированным (как например в ЖЖ), где можно добавить человека в друзья, без того чтобы он добавлял вас. Если же он да добавит вас вы будете «взаимными друзьями». То есть будет существовать два ребра: (Он, Вы) и (Вы, Он)
Ещё одно из применений графа, которое я уже упоминал это ссылки с сайта на сайт. Представим Вы хотите сделать поисковую систему и хотите учесть на какие сайты есть больше ссылок (например сайт A), при этом учитывать сколько сайтов ссылается на сайт B, который ссылается на сайт A. У вас будет матрица смежности этих ссылок. Вы захотите ввести какую то систему подсчёта рейтинга, которая делает какие то подсчёты на этой матрице, ну, а дальше… это Google (точнее PageRank) =)

Заключение

Это небольшая часть теории которая понадобится нам чтобы для следующих частей. Надеюсь вам было понятно, а главное понравилось и заинтересовало читать дальнейшие части! Оставляйте свои отзывы и пожелания в комментариях.

В следующей части

BFS — Алгоритм поиска в ширину

Библиография

Кормен, Лайзерсон, Риверст, Штайн — Алгоритмы. Построение и анализ. Издательство Вильямс, 2007.
Словарь терминов теории графов
Граф — статья в английской Википедии

Статья это кросс-пост из моего блога — «Programing as is — записки программиста»

Источник

Графы. Способы представления графа в программе

В качестве простейшего примера графа часто приводят систему дорог между городами, где города — это вершины, а дороги — ребра графа. Однако, вокруг нас есть множество и более обыденных примеров:

• электрическая схема является графом, в котором вершины — элементы схемы, а дуги — соединяющие провода;
• блок-схема алгоритма;
• система каталогов операционной системы является частным случаем графа — каталоги и папки задаются вершинами, а отношение вложенности — дугами.

Если направление ребер графа имеет значение (например при отражение отношения вложенности каталогов) — то граф называется ориентированным. Если направление не важно (например при соединении элементов электрической цепи) — граф является неориентированным. Кроме того, ребрам часто приписывается вес, граф в этом случае называется взвешенным — в системе дорог веса ребер могут отражать расстояния между городами.

В связи с этим возникает необходимость обработки графов компьютером, но для этого необходимо сначала каким-то удобным для обработки образом разместить его в памяти. Итак, граф ( G ) — это совокупность вершин ( V ), и дуг ( E ), в зависимости от того, как они задаются, выделяются следующие способы машинного представления графа:

• матрица смежности для графа из N вершин хранится в виду двумерного массива размером N x N . Вершины графа в этом случае задаются номерами (индексами строк и столбцов матрицы), а ячейка графа matrix[i, j] отражает наличие дуги между соответствующими вершинами. Например, при наличии дуги в ячейке может быть записана единица (или вес ребра i->j для взвешенного графа) , а при отсутствии — ноль;
• матрица инцидентности для графа из N вершин и M дуг хранится в виде двумерного массива размером N x M . Ячейка матрицы matrix[i, j] отражает инцидентность ребра j вершине i , т.е. тот факт, что это ребро выходит или входит в вершину i . Если ребро не связано с вершиной — в соответствующей ячейке матрицы записывается ноль, в противном случае единица (если граф ориентированный, то начало ребра можно отметить -1 , а конец 1 , если граф взвешенный — единица может быть заменена весом соответствующего ребра).

A	B	C	D	E	F	G
A	0	12	0	0	0	16	3
B	12	0	8	0	0	0	6
C	0	8	0	4	0	0	8
D	0	0	4	0	14	0	30
E	0	0	0	14	0	28	11
F	16	0	0	0	28	0	13
G	3	6	8	30	11	13	0

Матрица инцидентности графа:

AB	BC	CD	DE	EF	FA	AG	BG	CG	DG	EG	FG
A	12	0	0	0	0	0	3	0	0	0	0	0
B	12	8	0	0	0	0	0	6	0	0	0	0
C	0	8	4	0	0	0	0	0	8	0	0	0
D	0	0	4	14	0	0	0	0	0	30	0	0
E	0	0	0	14	28	0	0	0	0	0	11	0
F	0	0	0	0	28	16	0	0	0	0	0	13
G	0	0	0	0	0	16	3	6	8	30	11	13

Работая с приведенными матрицами возможно, например, найти в графе кратчайшие пути между вершинами, построить минимальные остовы и т.д., однако, у них есть недостатки:

• избыточность. Зачастую в графах ребра существуют между небольшим (количеством вершин), поэтому в матрице смежности будет огромное количество нулей. В матрице инцидентности в каждом столбце может быть лишь два ненулевых значения (т.к. у дуги два конца). На хранение нулей тратится память, что может быть существенно при обработки больших графов;
• недостаточная расширяемость. В матрицу смежности можно без проблем добавлять новые дуги, но чтобы добавить вершину нужно создавать новую матрицу большего размера и копировать в нее данные из старой. Это работает очень медленно при больших матрицах. В матрице инцидентности такие проблемы возникнут как при добавлении дуг, так и при добавлении вершин.

В связи с этим, зачастую применяются списки смежности и инцидентности. Для каждой вершины при этом хранится список с номерами смежных вершин или инцидентных ребер. В качестве структуры данных при этом могут использоваться массивы, связные списки и даже хеш-массивы.

A	B(12)	F(16)	G(3)
B	A(12)	C(8)	G(6)
C	B(8)	D(4)	G(8)
D	C(4)	E(14)	G(30)
E	D(14)	F(28)	G(11)
F	A(16)	E(28)	G(13)
G	A(3)	B(6)	C(8)	D(30)	E(11)	F(13)

Списки смежности и инцидентности решают проблему расширяемости графа, т.к. новые узлы и дуги могут быть очень просто и эффективно добавлены во время выполнения программы, кроме того они более оптимальны по памяти, т.к. хранятся только данные о существующих дугах. Однако, такой способ представления графа менее эффективен по процессорному времени, т.к. для проверки существования дуги в худшем случае нужно будет перебрать все дуги, выходящие из некоторой вершины, но в матрице смежности было достаточно обратиться к элементу массива (асимптотическая сложность ухудшилась с O(1) до O(K) при использовании связных списков или O(log(K)) при использовании хеш-массивов). Важно, что K в этом случае — количество смежных вершин, для многих графов оно не будет очень большим (например, если граф представлял бы карту города, то скорее всего значение K для каждой вершины не превышало бы 4-6 ), в связи с этим, нужно очень внимательно выбирать структуру данных для хранения списков смежности/инцидентности.

Еще одним способом задания графа в программе может быть хранение указателей на смежные вершины/инцидентные дуги внутри каждого узла программы, при этом узел описывается в виде структуры, содержащей данные и эти указатели. Примерно так:

Сам граф в программе хранится в виде списка таких вершин.

Литература по теме:

• Анализ сложности алгоритмов. Примеры — поможет разобраться с оценкой сложности по памяти и процессорному времени (нужно чтобы уметь выбирать наиболее подходящую для своей задачи структуру данных);
• Макоха А. Н., Сахнюк П. А., Червяков Н. И. Дискретная математика: Учеб. пособие. — М. ФИЗМАТЛИТ, 2005 — 368 с.
• Дж. Макконелл Анализ алгоритмов. Активный обучающий подход. — 3-е дополненное издание. М: Техносфера, 2009. -416с.

Источник