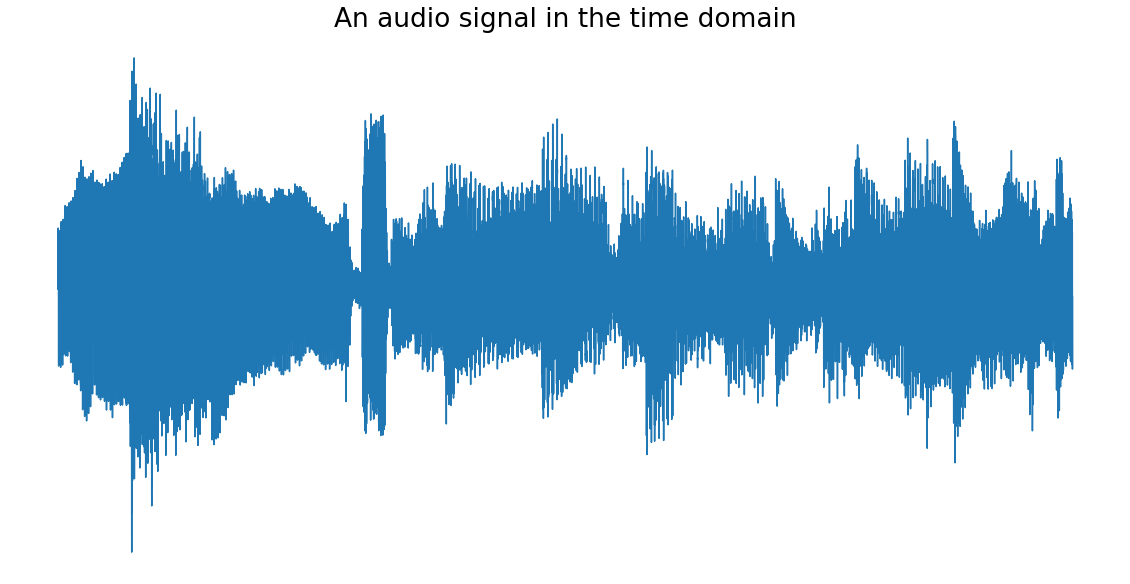- Спектральный анализ сигналов нелинейных звеньев АСУ на Python
- Метод анализа и программный код
- Результаты
- Вывод
- Модуль scipy.fft
- Зачем может понадобиться преобразование Фурье?
- Временная область против частотной области
- Классификация преобразований Фурье
- Практический пример: удаление нежелательного шума из аудиофайла
- Создание сигнала
- Фильтрация сигнала
- Применение обратного преобразования Фурье
- Заключение
Спектральный анализ сигналов нелинейных звеньев АСУ на Python
В моей статье [1] рассмотрен метод гармонической линеаризации для исследования систем управления, содержащих нелинейные элементы.
Этот метод может быть использован в том случае, когда линейная часть системы является низкочастотным фильтром, т.е. отфильтровывает все возникающие на выходе нелинейного элемента гармонические составляющие, кроме первой гармоники [2]. Поэтому логическим продолжением моей первой статьи будет гармонический анализ рассмотренных нелинейных элементов. Кроме этого нужно рассмотреть аппаратную альтернативу методу гармонической линеаризации.
Метод анализа и программный код
Пусть на нелинейные элементы поступает чистый синусоидальный сигнал. Методом разложения в дискретный ряд Фурье получим его спектр.
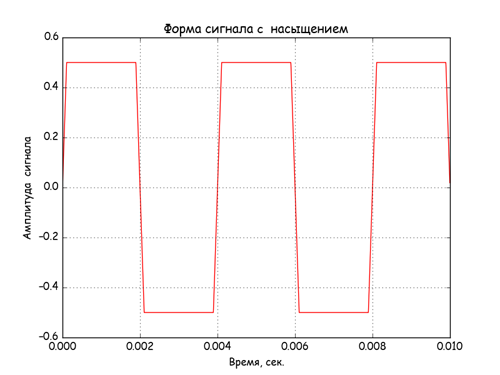
#!/usr/bin/env python #coding=utf8 from numpy import array, arange, abs as np_abs from numpy.fft import rfft, rfftfreq from math import sin, pi import matplotlib.pyplot as plt import matplotlib as mpl mpl.rcParams['font.family'] = 'fantasy' mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial' FD = 250000#частота дискретизации, отсчётов в секунду N = 2500#длина входного массива, N/FD секунд F=250.0#циклическая частота входного сигнала w=(2.*pi*F/FD)#отсчёт круговой частоты A=3.0#амплитуда сигнала B=0.5#порог ограничения #сгенерируем чистый синусоидальный сигнал с частотой F длиной N sin_sig = array([A*sin(w*t) for t in range(N)])#график сигнала plt.plot(arange(N)/float(FD), sin_sig, 'r') plt.xlabel('Время, сек.') plt.ylabel('Амплитуда сигнала') plt.title('Входной синусоидальный сигнала') plt.grid(True) plt.show() spectr_sin = rfft(sin_sig )#вычисляем дискретное действительное rfft преобразование Фурье plt.plot(rfftfreq(N, 1./FD), np_abs(spectr_sin)/N) #график спектра plt.xlabel('Частота, Гц') plt.ylabel('Амплитуда сигнала') plt.title('Спектр синусоидального сигнала') plt.grid(True) plt.show() Получим сигнал и спектр сигнала с выхода нелинейного элемента с «насыщением».
# сгенерируем сигнал нелинейности c «насыщением» из A*sin(w*t) при abs(А)>abs(B) sinp_sig =array([A*sin(w*t) if abs(A*sin(w*t)) Для учёта знака ограничения B использован следующий код — A*sin(w*t)*B/abs(A*sin(w*t).
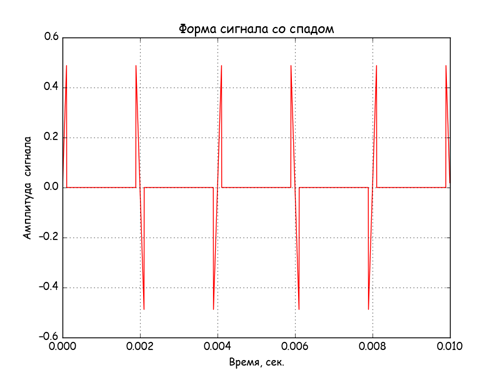
Получим вид сигнала и спектр нелинейного элемента с переходом амплитуды в ноль.
# сгенерируем сигнал нелинейности «cо спадом до нуля» из A*sin(w*t) при abs(А)=abs(B) sinn_sig = array([A*sin(w*t) if abs(A*sin(w*t)) Результаты
Сигнала на входе и на выходе нелинейных элементов.
Спектры сигналов на выходе нелинейных элементов.
Нелинейный элемент со спадом сигнала генерирует большое число высокочастотных гармоник. Для фильтрации сигнала на выходе нелинейных элементов можно применить цифровой НЧ фильтр, детально описанный в работе [3]. Для исследования возможностей цифровой фильтрации сигналов нелинейных элементов в код программы [3], были внесены следующие изменения.
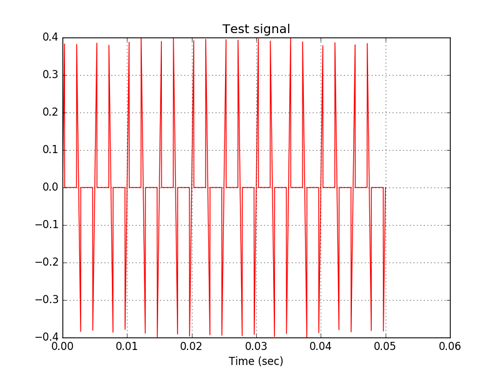
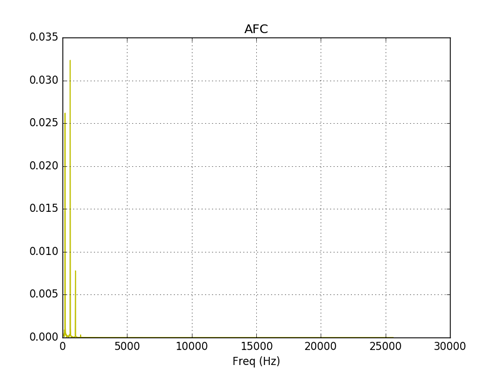
A=1.0 B=0.4 test_n = 2560 # Кол-во отсчётов тестового сигнала test_f = 200 # Наименьшая отличная от нуля частота тестового сигнала test_period_count = 10.0 # Кол-во периодов тестового сигнала test_t = numpy.linspace(0.0, test_period_count/test_f, test_n) # Базовый сигнал sin(wt), подлежащий восстановлению фильтром test_base_signal = array([A*sin(2*pi*test_f* i) for i in test_t ]) test_signal =array([A*sin(2*pi*test_f* i) if abs(sin(2*pi*test_f* i)) Спектр сигнала на выходе фильтра.
Вывод
Решить задачу использования нелинейных элементов можно аппаратно используя микропроцессор, но при этом необходимо согласование уровней сигналов, а так же ЦАП и АЦП.
Модуль scipy.fft
Прежде чем начать, необходимо установить SciPy, NumPy (библиотека для работы с массивами) и Matplotlib (библиотека для визуализации данных). Вы можете сделать это одним из двух способов:
- С помощью Anaconda: загрузите и установите Anaconda Individual Edition. В этот набор инструментов уже включены перечисленные библиотеки.
- С помощью pip вы можете установить (или обновить) библиотеки посредством следующей команды:
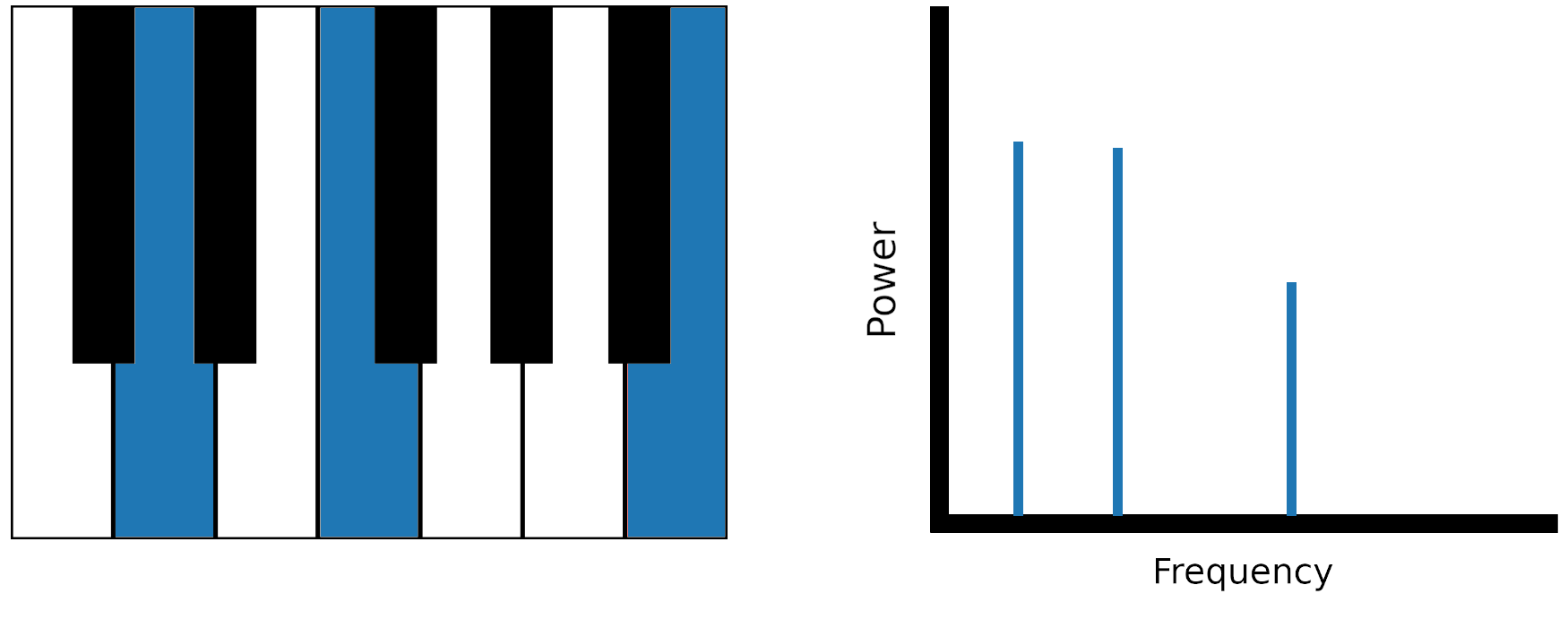
Представьте, что вы использовали преобразование Фурье для записи того, как кто-то играет на фортепиано аккорд из трёх нот.
Результирующий частотный спектр покажет три пика – по одному для каждой ноты. Если человек играл одну ноту мягче, мощность для частоты этой ноты будет меньше, чем для двух других.
Зачем может понадобиться преобразование Фурье?
Преобразование Фурье полезно во многих приложениях. Например, Shazam и другие службы распознавания музыки используют преобразование Фурье для идентификации песен. Алгоритм сжатия JPEG представляет собой вариант преобразования Фурье, применяемый для удаления высокочастотных компонент изображений. В распознавании речи преобразование Фурье и связанные с ним преобразования служат для восстановления произнесенных слов.
Задача преобразования Фурье возникает всякий раз, когда нужно как-либо работать с сигналом, представляемым в пространстве частот.
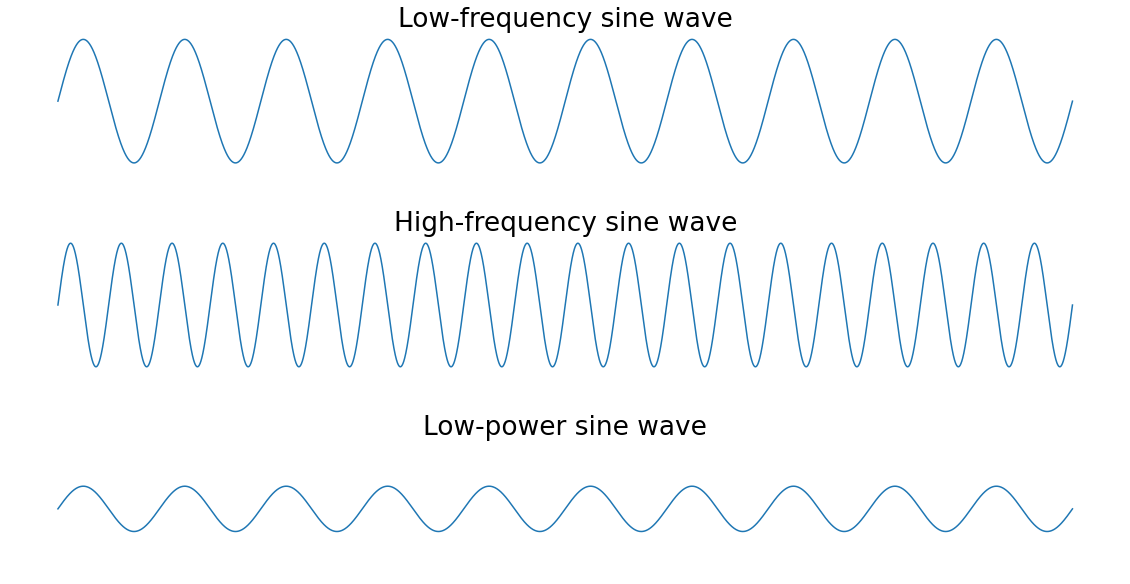
Временная область против частотной области
Далее мы будем иметь дело с временно́й и частотной областями] – двумя подходами к представлению сигнала: как информации, которая изменяется во времени и информации, отображенной в виде набора частот и соответствующих им амплитуд.
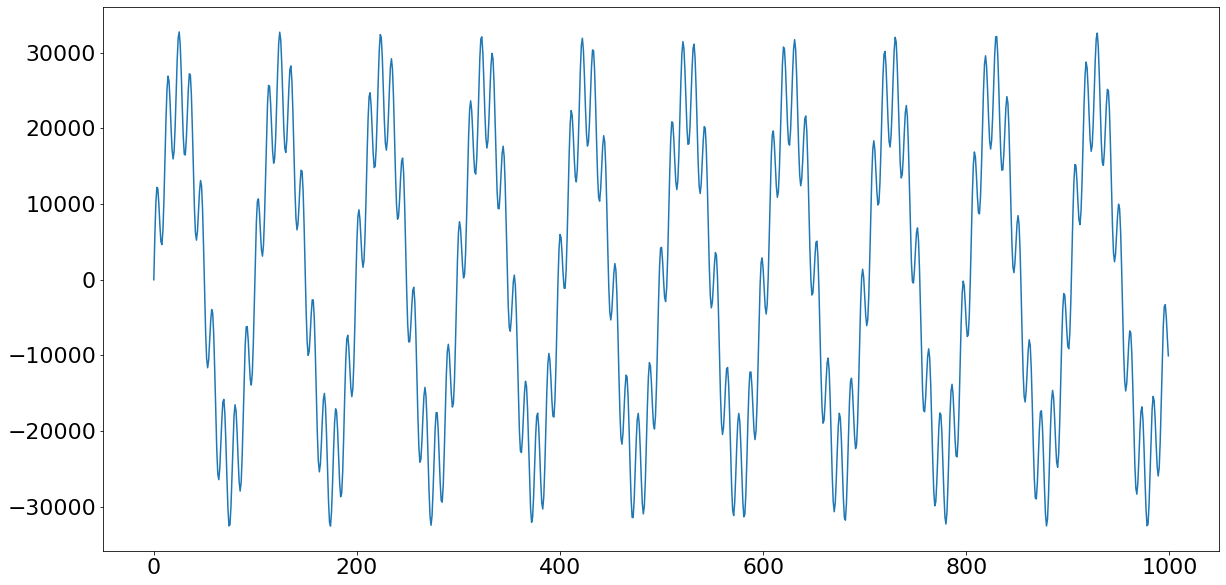
Ниже представлено характерное изображение аудиосигнала – классического примера сигнала во временной области. Горизонтальная ось соответствует времени, вертикальная ось – амплитуде.
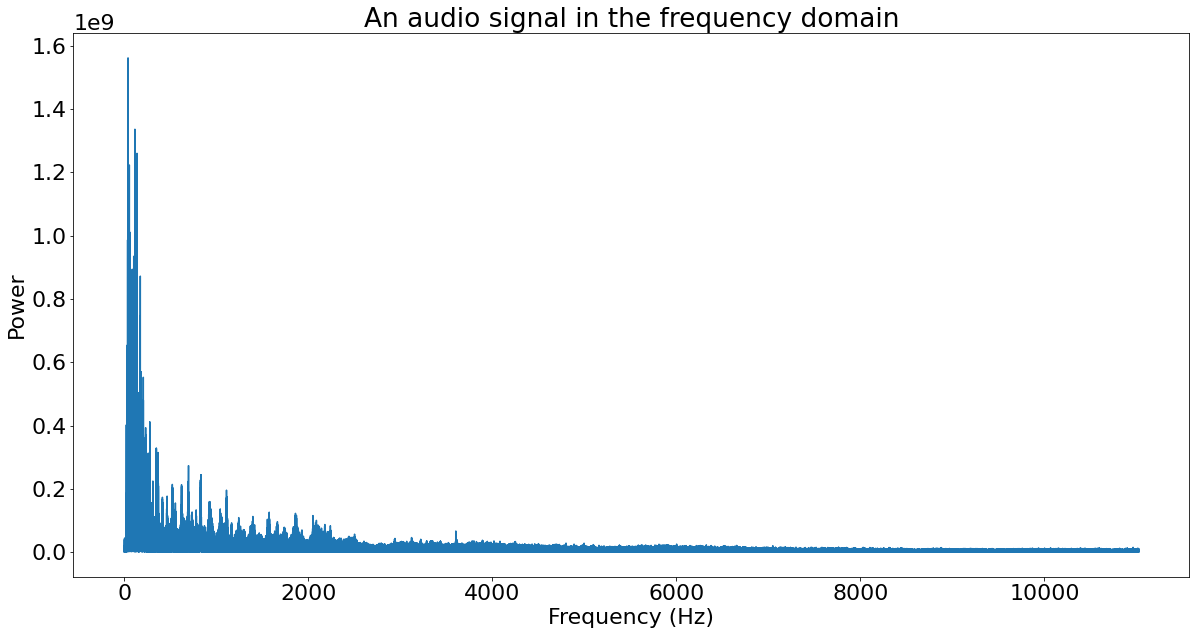
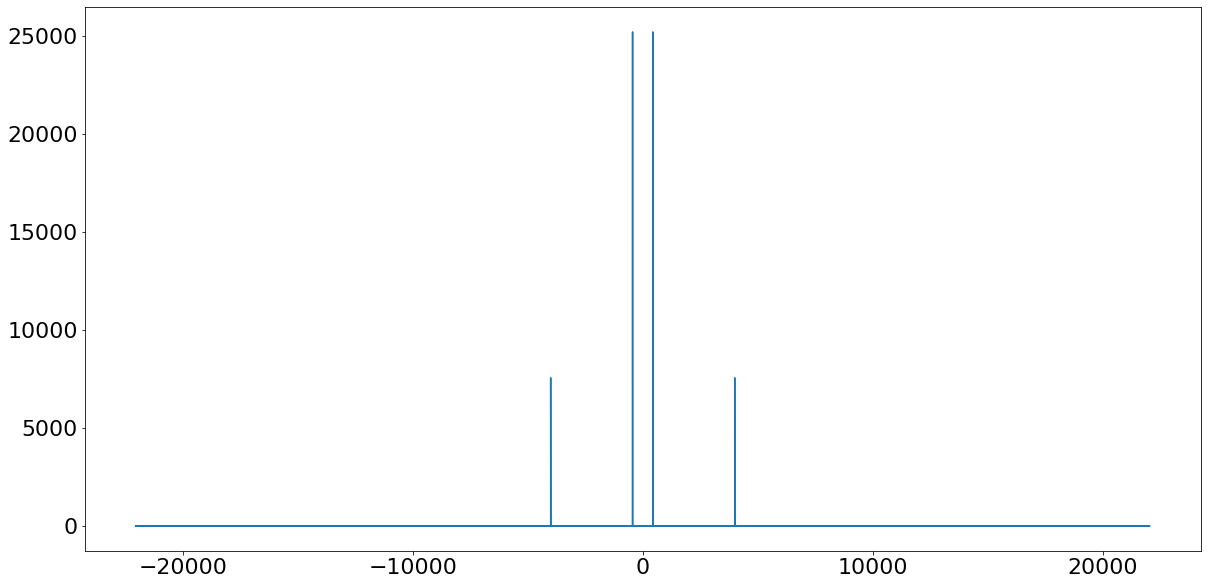
Тот же звуковой сигнал можно представить разложенным по составляющим его частотам. Горизонтальная ось на рисунке ниже представляет частоту, вертикальная ось – мощность.
Классификация преобразований Фурье
Преобразование Фурье подразделяют на категории по нескольким признакам. В первую очередь – по типу функций, с которыми работает преобразование: непрерывные или дискретные. В этом руководстве мы рассматриваем дискретное преобразование Фурье (DFT).
Термины DFT и FFT нередко используются как взаимозаменяемые. Однако это не совсем одно и то же: быстрое преобразование Фурье (FFT) – лишь один из алгоритмов вычисления дискретного преобразования Фурье.
Еще одна линия раздела в терминологии, с которым вы столкнетесь при использовании scipy.fft ,– разные типы ввода. Например, функция fft() принимает комплексные числа, а rfft() работает только с действительными числами. В дальнейшем мы обсудим это подробнее.
Практический пример: удаление нежелательного шума из аудиофайла
Чтобы лучше понять преобразование Фурье и то, как его можно применить, решим задачу фильтрации звука. Намеренно создадим звуковой сигнал с высокочастотным шумом, а затем удалим шум с помощью преобразования Фурье.
Создание сигнала
Одиночное гармоническое (синусоидальное) колебание представляют одну частоту и в музыкальном отношении является чистым тоном. Воспользуемся свойством таких волн для генерации звука:
Деление mixed_tone на максимальное значение масштабирует его в интервале от -1 до 1 . Умножение на 32767 масштабирует сигнал между -32767 и 32767 , что примерно соответствует диапазону np.int16 . Код отображает только первые 1000 точек, чтобы мы могли четче проследить структуру сигнала. Видимая нами синусоидальная волна – это сгенерированный тон 400 Гц, искаженный тоном 4000 Гц.
Чтобы прослушать звук, необходимо сохранить его в формате, который может прочитать аудиоплеер. Воспользуемся методом SciPy wavfile.write и сохраним результат в файле формата WAV. Выбранное нами 16-битное целочисленное представление является стандартным типом данных для wav-файлов.
На построенном спектре видны два пика на положительных частотах и два их зеркальных отражения в отрицательной области. Пики положительных частот находятся на позициях 400 и 4000 Гц.
Преобразование Фурье взяло колеблющийся сигнал и разложило его по содержащимся в нем частотам. Поскольку мы сами внесли только две частоты, на выходе преобразования мы видим только их. Симметричное представление в положительной и отрицательной областях – побочный эффект ввода действительных значений в преобразование Фурье, о чём мы поговорим подробнее в дальнейшем.
Самый важный раздел в этом небольшом скрипте – вычисление преобразования Фурье:
Фильтрация сигнала
Самая замечательная вещь в преобразовании Фурье заключается в том, что оно обратимо. Любой сигнал, измененный в частотной области, можно преобразовать обратно во временную область. Воспользуемся этим, чтобы отфильтровать высокочастотный шум.
Возвращаемые rfft() значения соответствуют мощности каждого частотного бина. Если мы установим мощность бина равной нулю, соответствующая частота перестанет присутствовать в результирующем сигнале во временной области:
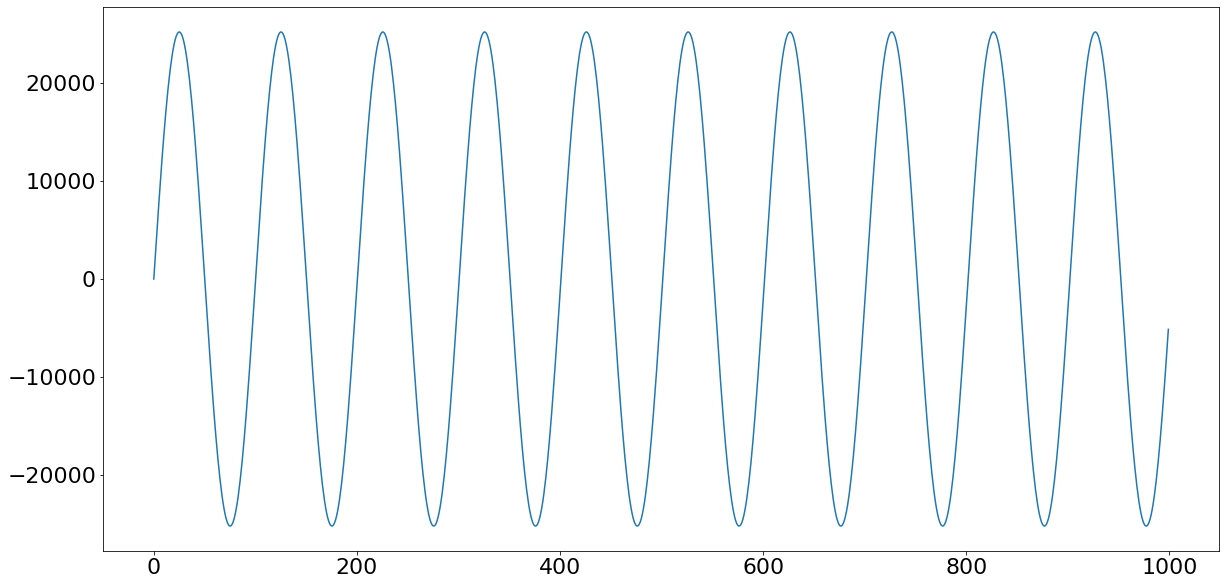
Остался только один пик. Применим обратное преобразование Фурье, чтобы вернуться во временную область.
Применение обратного преобразования Фурье
Применение обратного FFT аналогично применению FFT:
Поскольку мы использовали rfft() , для обратного преобразования нужно использовать irfft() . Однако, если бы мы использовали fft() , обратной функцией была бы ifft() .
Как видите, теперь есть одна синусоида, колеблющаяся с частотой 400 Гц – мы успешно удалили шум на 4000 Гц.
Нормализуем сигнал и запишем результат в файл. Сделать это можно так же, как в прошлый раз:
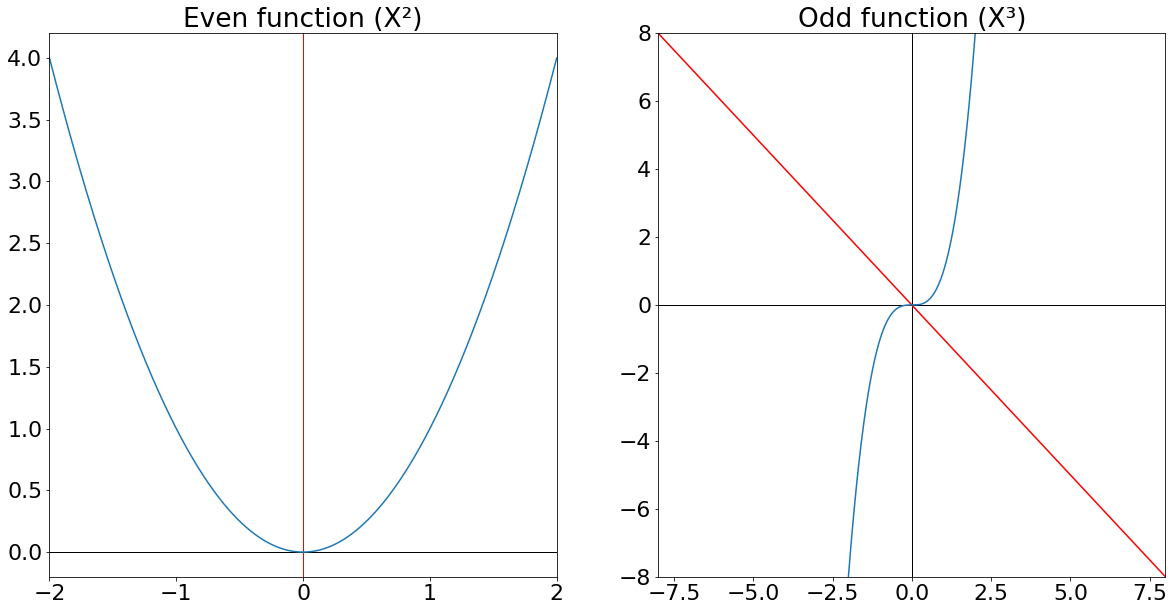
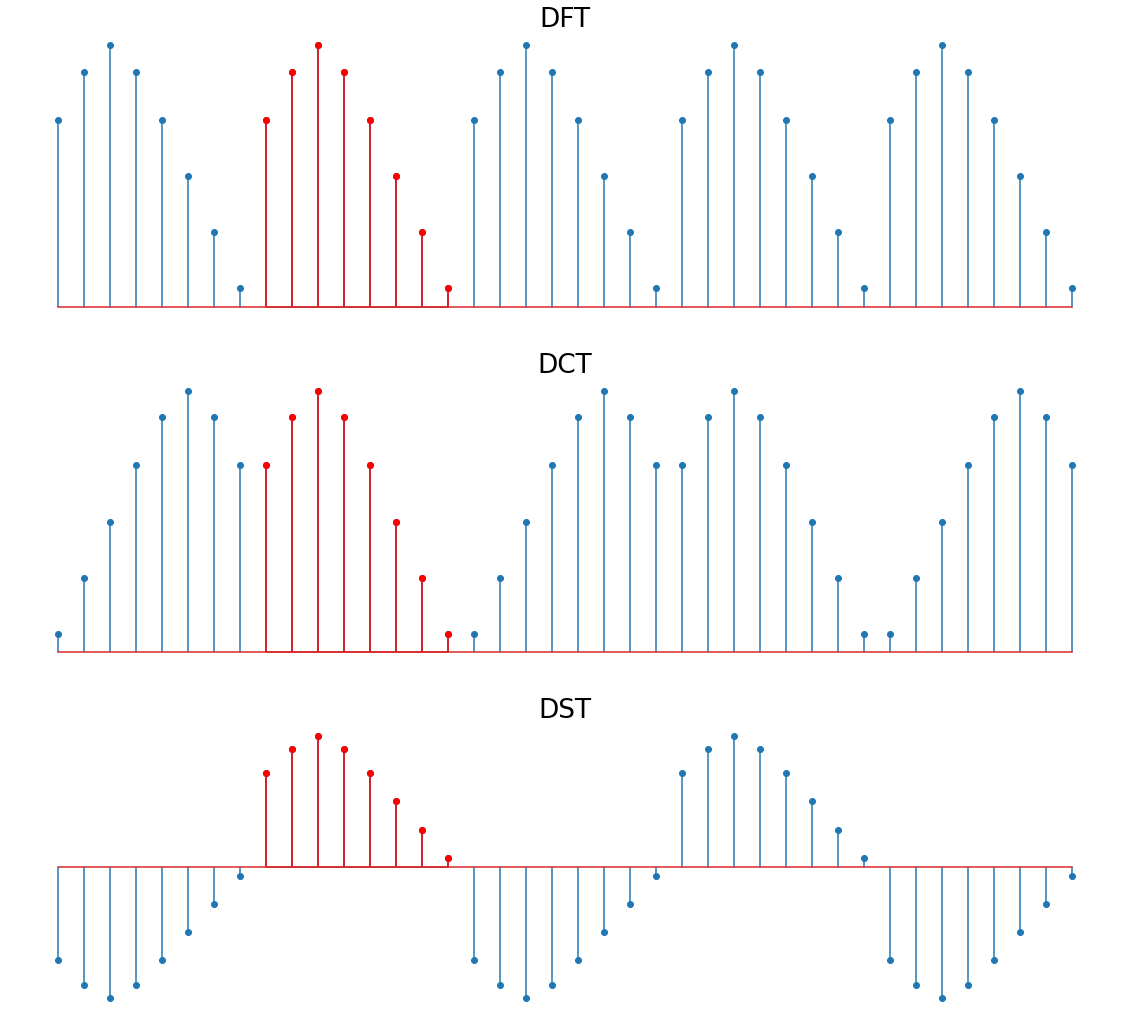
При расчете полного преобразования Фурье (DFT) предполагается, что функция, по которой происходит вычисление, повторяется бесконечно. Однако преобразования DCT и DST позволяют учесть симметрию сигнала. Косинусное преобразование (DCT) предполагает, что функция продлевается за счет четной симметрии, а для DST – за счет нечетной симметрии.
На следующем изображении показано, как каждое преобразование представляет, как функция будет продолжаться в бесконечности.
На изображении выше полное преобразование повторяет функцию как есть. DCT отражает функцию по вертикали, а DST – по горизонтали. Обратите внимание, что симметрия DST приводит к существенным разрывам функции. Это вносит высокочастотные составляющие в результирующем частотном спектре. Если нет сведений о симметрии сигнала, лучше использовать DCT.
Есть множество примеров использования DCT в различных задачах, требующих высокой скорости преобразования Фурье, в том числе в алгоритмах JPEG, MP3 и WebM.
Заключение
Преобразование Фурье – это мощная концепция, применяемая в самых разных областях – от чистой математики до аудиотехники и даже финансов. В этом уроке мы рассмотрели:
- как и когда используется преобразование Фурье
- как выбрать нужную функцию из scipy.fft
- в чем разница между временной и частотной областями
- как посмотреть и изменить частотный спектр сигнала
- как использовать rfft() , чтобы преобразование выполнялось еще быстрее
Мы рассмотрели только базовую идею, но ее понимание поможет разобраться в других вопросах, связанных с преобразованием Фурье и представлением функций в виде частотных спектров.
Больше полезной информации вы можете получить на нашем телеграм-канале «Библиотека питониста». Рекомендуем также обратить внимание на учебный курс по Python от «Библиотеки программиста».