Создание графов в python

Отображение графа на Python с networkx

Граф — это форма визуализации, позволяющая показывать и анализировать отношения между сущностями. Например, рисунок ниже показывает вклад редакторов Википедии на различных языках энциклопедии в июле 2013 года:

Можно сделать несколько наблюдений:

• Английский (en) — основной язык, на который переводятся все остальные языки; в то же время многие англоязычные материалы переводятся на другие языки.
• Китайский (zh) переводится на японский (ja), но не наоборот.
• И китайский, и японский материалы переведены на английский, и наоборот.

Я же расскажу о том, как для отображения графов использовать пакет networkx.

Установка networkx

Чтобы установить этот пакет, используйте команду pip:

Терминология

Прежде чем начать отрисовку графа, полезно знать некоторые основы.
На рисунке ниже показывается направленный граф, также известный как диграф, ребра которого имеют обозначенные стрелками направления.

• Узел — фундаментальный элемент графа, общеизвестный под названием вершина.
• Ребро — соединение узлов графа.
• Неориентированный граф не имеет направления между узлами, то есть не имеет стрелок, а его ребра двунаправлены.

Создание графа

Давайте шаг за шагом создадим граф.

Во-первых, создадим объект класса networkx.classes.graph.Graph:

import networkx as nx G = nx.Graph() print(G) # Graph with 0 nodes and 0 edges

Класс nx.Craph() создает неориентированный граф. Если захочется создать ориентированный, используйте класс nx.DiGraph(directed=True), который возвращает объект networkx.classes.digraph.DiGraph.

В этой статье поговорим об ориентированных графах.

Добавим узлы

Фрагмент кода ниже добавляет три узла без ребер:

G.add_node("Singapore") G.add_node("San Francisco") G.add_node("Tokyo") print(G) # Graph with 3 nodes and 0 edges

Помимо функции add_node() для добавления индивидуальных узлов, чтобы добавить множество узлов, можно воспользоваться функцией add_nodes_from():

G.add_nodes_from(["Riga", "Copenhagen"]) print(G) # Graph with 5 nodes and 0 edges

Добавим ребра

Теперь, когда узлы определены, определим ребра, чтобы соединить их:

G.add_edge("Singapore","San Francisco") G.add_edge("San Francisco","Tokyo") G.add_edges_from( [ ("Riga","Copenhagen"), ("Copenhagen","Singapore"), ("Singapore","Tokyo"), ("Riga","San Francisco"), ("San Francisco","Singapore"), ] ) print(G) # Graph with 5 nodes and 6 edges

Как и узлы, ребра можно добавлять по одному, при помощи add_edge(), или группами — при помощи add_edges_from() со списком кортежей, представляющих каждый узел.

Рисуем граф

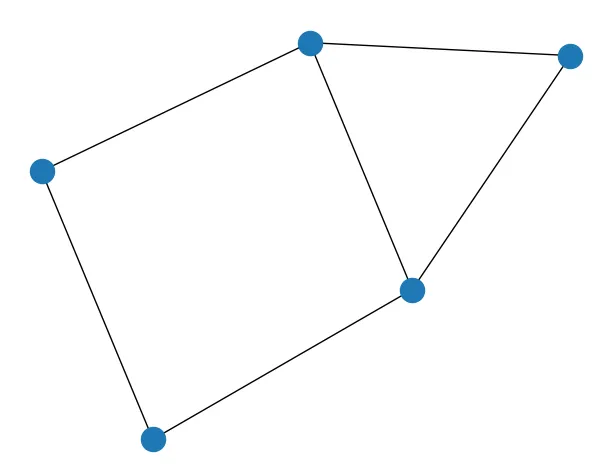
Я покажу основы отображения сетевых графов при помощи пакета networkx. Начнем:

Вот другое изображение того же графа:

Отображение меток

Само собой, граф без меток не очень полезен, если вообще полезен, поэтому давайте отрисуем метки:

nx.draw(G, with_labels = True)

• nx.draw_networkx_nodes() — рисует все узлы графа;
• nx.draw_networkx_labels() — рисует метки на каждом узле;
• nx.draw_networkx_edges() — рисует ребра, соединяющие узлы.

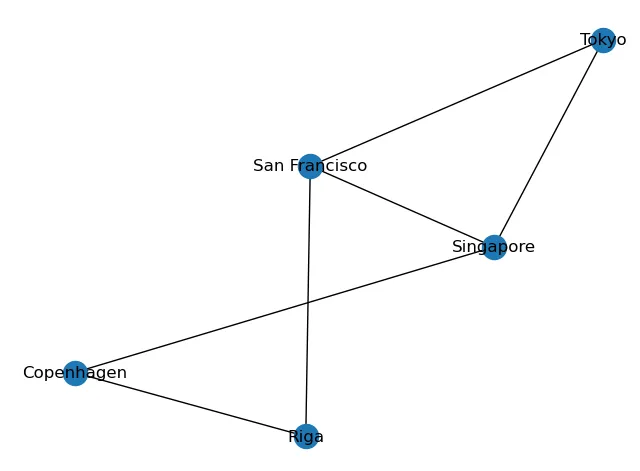
И теперь мы видим метку каждого узла:

Применение макетов

Помните, что функция draw() каждый раз использует разные макеты? Так вот, для графа можно указать конкретный макет:

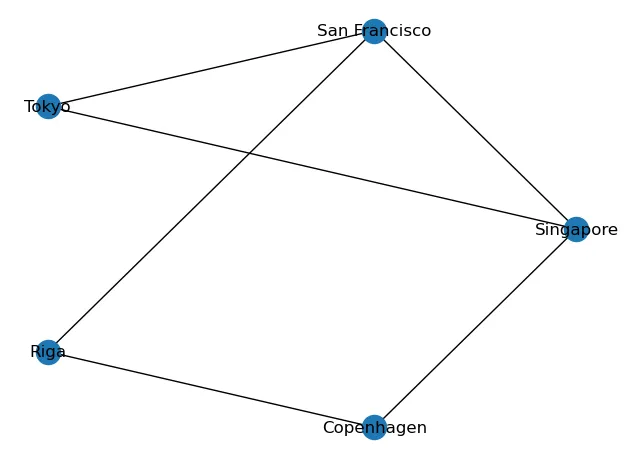
pos = nx.circular_layout(G) nx.draw(G, pos, with_labels = True)

Узлы упорядочены так, что по ним можно очертить круг:

Кроме того, график с круговой компоновкой можно нарисовать с помощью nx.draw_circular(), а не nx.draw():

nx.draw_circular(G, with_labels = True)

Можно попробовать другие макеты:

• nx.draw_kamada_kawai(G, with_labels = True);
• nx.draw_planar(G, with_labels = True);
• nx.draw_random(G, with_labels = True);
• nx.draw_spectral(G, with_labels = True);
• nx.draw_spring(G, with_labels = True);
• nx.draw_shell(G, with_labels = True);

Разметка ребер

Ребра можно отметить при помощи nx.draw_networkx_edge_labels(). Фрагмент кода ниже размечает два ребра трех узлов:

pos = nx.circular_layout(G) nx.draw(G, pos, with_labels = True) nx.draw_networkx_edge_labels( G, pos, edge_labels=< ("Singapore","Tokyo"): '2 flights daily', ("San Francisco","Singapore"): '5 flights daily', >, font_color='red' )

Ориентированный граф

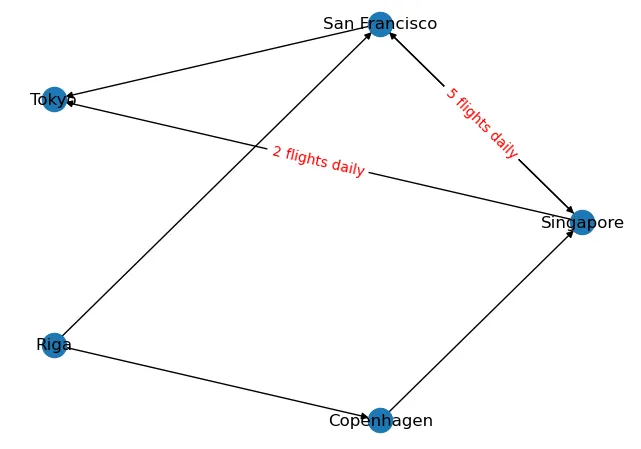
Иногда полезно построить ориентированный граф. В нашем примере ребра могут представлять рейсы между двумя городами. Ориентированный граф позволяет увидеть, какие рейсы идут из одного города в другой. Следующий фрагмент кода показывает наш пример в виде ориентированного графа:

import networkx as nx #---directed graph--- G = nx.DiGraph(directed=True) # add nodes G.add_node("Singapore") G.add_node("San Francisco") G.add_node("Tokyo") G.add_nodes_from(["Riga", "Copenhagen"]) # add edges G.add_edge("Singapore","San Francisco") G.add_edge("San Francisco","Tokyo") G.add_edges_from( [ ("Riga","Copenhagen"), ("Copenhagen","Singapore"), ("Singapore","Tokyo"), ("Riga","San Francisco"), ("San Francisco","Singapore"), ] ) # set layout pos = nx.circular_layout(G) # draw graph nx.draw(G, pos, with_labels = True) # draw edge labels nx.draw_networkx_edge_labels( G, pos, edge_labels=< ("Singapore","Tokyo"): '2 flights daily', ("San Francisco","Singapore"): '5 flights daily', >, font_color='red' )

Теперь вы видите, что есть рейсы из Сингапура в Сан-Франциско и наоборот; с другой стороны, есть рейсы из Риги в Сан-Франциско, но не наоборот:

Настройка узлов

По умолчанию узлы имеют синий цвет и довольно маленький размер. Настроить узлы и цвет ребра можно, передав словарь в функцию draw():

options = < 'node_color': 'yellow', # color of node 'node_size': 3500, # size of node 'width': 1, # line width of edges 'arrowstyle': '-|>', # array style for directed graph 'arrowsize': 18, # size of arrow 'edge_color':'blue', # edge color > nx.draw(G, pos, with_labels = True, arrows=True, **options)

Сейчас узлы желтые и они больше, а ребра синие:

Очерчивание узлов

Если вы хотите обозначить узлы, вам нужно сделать это вручную, используя matplotlib. Следующий фрагмент кода задает размер рисунка 10 на 10 дюймов (ширина и высота), а затем функцией set_edgecolor() рисует контур каждого узла:

pos = nx.circular_layout(G) options = < 'node_color': 'yellow', 'node_size': 8500, 'width': 1, 'arrowstyle': '-|>', 'arrowsize': 18, > nx.draw(G, pos, with_labels = True, arrows=True, **options) ax = plt.gca() ax.collections[0].set_edgecolor("#000000")

Теперь каждый узел обведен черным:

Если не установить размер рисунка, граф будет выглядеть так:

Раскрашивание узлов

Чтобы раскрасить каждый узел разными цветами, можно определить цветовую палитру, такую как в bokeh, и установить значение ключу словаря node_color, затем передав его в draw():

from networkx import * import matplotlib.pyplot as plt from bokeh.palettes import Spectral plt.figure(figsize=(8, 8)) pos = nx.circular_layout(G) options = < 'node_color': Spectral[5], # first 5 colors from the Spectral palette 'node_size': 8500, 'width': 1, 'arrowstyle': '-|>', 'arrowsize': 18, > nx.draw(G, pos=pos, with_labels = True, arrows=True, **options) ax = plt.gca() ax.collections[0].set_edgecolor("#000000")

И теперь узлы графа раскрашены разными цветами:

Если захочется указать свой цвет, установите его вручную:

Вот и все на сегодня. А на наших курсах — полезная теория и много практики:

Data Science и Machine Learning

Python, веб-разработка

Мобильная разработка

От основ — в глубину

Источник

работа с графами в Python

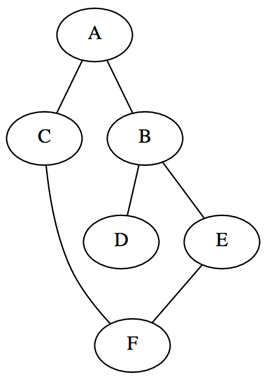
Будет использоваться ненаправленный связный граф V=6 E=6. Существует две популярные методики представления графов: матрица смежности (эффективна с плотными графами) и список связей (эффективно с разряженными графами). Будем использовать второй способ.

graph = 'A': ['B', 'C'], 'B': ['A', 'D', 'E'], 'C': ['A', 'F'], 'D': ['B'], 'E': ['B', 'F'], 'F': ['C', 'E']>

2 Depth-First Search — Поиск вглубину

Алгоритм поиска вглубину: исследуем сначала все возможные вершины (из выбранного корня) доступные из текущей, прежде чем возвращаться назад. Данный алгоритм можно реализовать как рекурсивно, так и итеративно. Последовательность действий:

• Помечаем текущую вершину как посещённую
• Исследуем каждую соседнюю вершину не включённую в список уже посещённых
• Вариант с DFS and BFS in Python (модифицированный, т.к. set не поддерживает упорядоченность элементов)

graph = 'A': ['B', 'C'], 'B': ['A', 'D', 'E'], 'C': ['A', 'F'], 'D': ['B'], 'E': ['B', 'F'], 'F': ['C', 'E']> def dfs(graph, start): visited, stack = [], [start] while stack: vertex = stack.pop() if vertex not in visited: visited.append(vertex) stack.extend(set(graph[vertex]) - set(visited)) return visited print(dfs(graph, 'A'))

• Вариант с DFS and BFS graph traversal (Python recipe) (модифицированный, т.к. для реализации стека нам необходимо добавлять элементы в конец списка, а не в начало)

graph = 'A': ['B', 'C'], 'B': ['A', 'D', 'E'], 'C': ['A', 'F'], 'D': ['B'], 'E': ['B', 'F'], 'F': ['C', 'E']> def iteractive_dfs(graph, start, path=None): """iterative depth first search from start""" if path is None: path = [] q = [start] while q: v = q.pop() if v not in path: path = path + [v] q += graph[v] return path print(iteractive_dfs(graph, 'A'))

3 DFS Paths — поиск пути между двумя вершинами

graph = 'A': ['B', 'C'], 'B': ['A', 'D', 'E'], 'C': ['A', 'F'], 'D': ['B'], 'E': ['B', 'F'], 'F': ['C', 'E']> def dfs_paths(graph, start, goal): stack = [(start, [start])] # (vertex, path) while stack: (vertex, path) = stack.pop() for next in set(graph[vertex]) - set(path): if next == goal: yield path + [next] else: stack.append((next, path + [next])) print(list(dfs_paths(graph, 'A', 'F')))

4 Bread-Firsth Search — Поиск вширину

Позволяет найти кратчайший путь между двумя вершинами. Довольно сложно реализовать рекурсивно, гораздо проще реализовать его с использованием очереди.

graph = 'A': ['B', 'C'], 'B': ['A', 'D', 'E'], 'C': ['A', 'F'], 'D': ['B'], 'E': ['B', 'F'], 'F': ['C', 'E']> from queue import deque def bfs(graph, start): visited, queue = [], deque([start]) while queue: vertex = queue.pop() if vertex not in visited: visited.append(vertex) queue.extendleft(set(graph[vertex]) - set(visited)) return visited print(bfs(graph, 'A'))

5 BFS Paths

from queue import deque graph = 'A': ['B', 'C'], 'B': ['A', 'D', 'E'], 'C': ['A', 'F'], 'D': ['B'], 'E': ['B', 'F'], 'F': ['C', 'E']> def bfs_paths(graph, start, goal): queue = deque([(start, [start])]) while queue: (vertex, path) = queue.pop() for next in set(graph[vertex]) - set(path): if next == goal: yield path + [next] else: queue.appendleft((next, path+[next])) print(list(bfs_paths(graph, 'A', 'F'))) def shortest_path(graph, start, goal): try: return next(bfs_paths(graph, start, goal)) except StopIteration: return None print(shortest_path(graph, 'A', 'F')) print(shortest_path(graph, 'E', 'D')) print(shortest_path(graph, 'A', 'D')) print(shortest_path(graph, 'F', 'D'))

[['A', 'C', 'F'], ['A', 'B', 'E', 'F']] ['A', 'C', 'F'] ['E', 'B', 'D'] ['A', 'B', 'D'] ['F', 'E', 'B', 'D']

Created: 2017-11-09 Thu 19:40

Источник