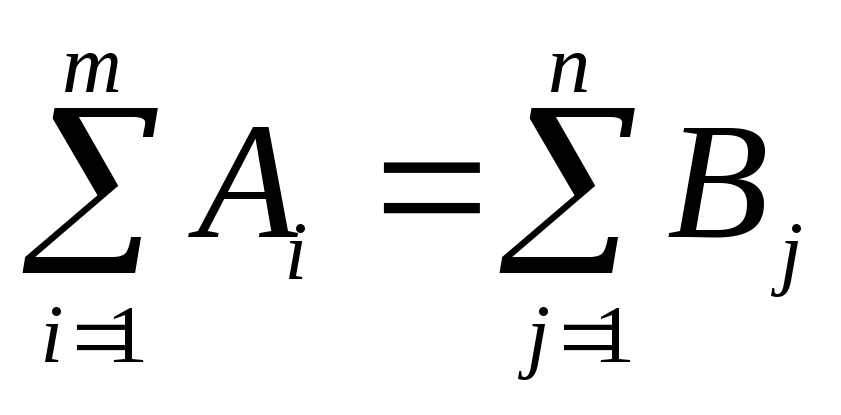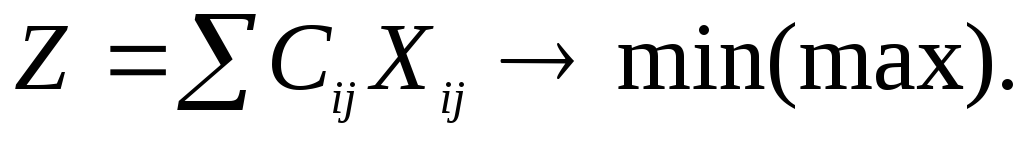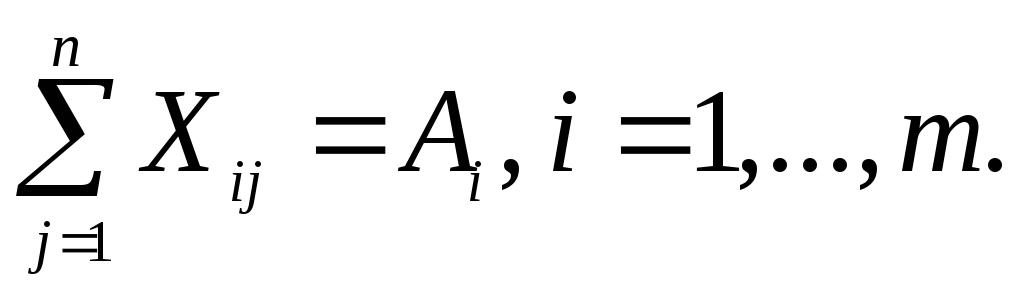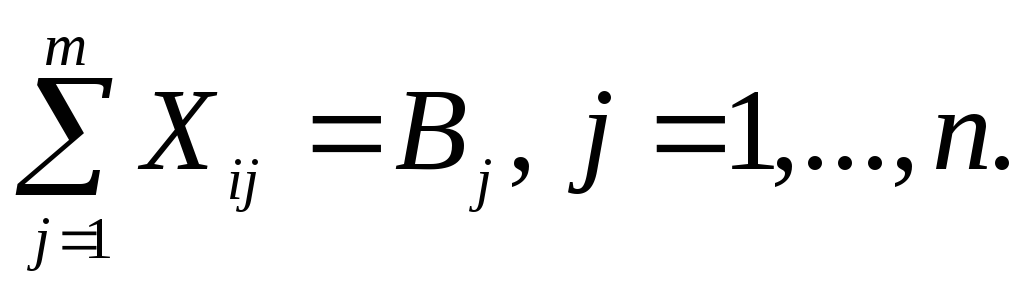Составные части моделей линейного программирования

Составные части общей модели линейного программирования

Вес модели линейного программирования состоят из стандартных составных частей: совокупность основных переменных, линейные 01раничения (условия), целевая функция, определяющая критерий оптимальности задачи.

Совокупность основных переменных характеризует размеры землепользований, площади, объемы производства, затраты материальных, трудовых, финансовых ресурсов.

Система линейных ограничений (условий) определяет область допустимых значений основных переменных. Каждое отдельное условие отражает реальное ограничение (нормы внесения удобрений, выполнение контрольных цифр бизнес-плана и т.д.).

Целевая функция представляется показателем, который обобщенно характеризует один из аспектов деятельности хозяйства данной землеустроительной задачи, например, чистый доход, валовую продукцию и т.д.

Критерий оптимальности в зависимости от условий задачи требует максимизации или минимизации целевой функции при заданных ограничениях.

В общем виде формализованная модель линейного программирования, построенная для решения задачи, в которой выделено N основных переменных *1. x_N и М ограничений, будет иметь следующий вид.

ПО где знак означает или , или =; константы b_t. b_M в правых частях ограничений предполагаются неотрицательными; требование неотрицательности основных переменных: х > 0, дг₂ > 0. Хщ > 0.

Совокупность ограничений и требований неотрицательности основных переменных определяет область допустимых значений задачи.

В кратком виде вышеприведенная развернутая запись будет следующей:

Распределительная модель линейного программирования

8.2. Распределительная модель линейного программирования

Распределительный метод среди задач линейного программирования получил распространение из-за упрощения расчетов, точности вычислений и снижения затрат времени на ввод исходной информации. Метод предложили А. Толстой и Л.В. Конгорович в 1939-1940 гг. Первоначально он применялся в задачах, связанных с транспортировкой грузов, их распределением между поставщиком и потребителем, поэтому получил название «транспортная задача». Применяется при решении ряда землеустроительных задач: распределение севооборотов и угодий по участкам, размещение культур па землях различных категорий, перераспределение участков между хозяйствами для экономии транспортных затрат и др.

Суть распределительной задачи следующая. Заданы /// источников ресурса (производители продукции, базы с готовой продукцией) и п пунктов его потребления. Запасы ресурса в источниках составляют A_hi= 1. //?, потребности — Bj, j= 1. п. Стоимость транспортировки единицы ресурса от /’-го источника к j-му потребителю С. Количество ресурса, транспортируемого от /-го источника к у-му потребителю Х_:1. Требуется определить такие значения Х,„ при которых общие транспортные расходы будут минимальны.

При сбалансированности, когда общий спрос на запас ресурса у поставщиков и общий спрос на него у потребителя равны, задачу называют закрытой:

Если баланс не выдерживается, то транспортная задача является открытой:

При наличии баланса модель транспортной задачи формулируется следующим образом.

Условия. СЬраничения но запасам:

Ограничения по потребностям:

Особенности распределительных транспортных задач следующие:

• • условия задачи описываются уравнениями (в симплекс-методе описываются и неравенствами);
• • все переменные выражаются в одних и тех же единицах измерения;
• • во всех уравнениях коэффициенты при переменных равны единице;
• • каждая переменная встречается только в двух уравнениях системы ограничений: в одном но строке (по запасам) и в одном но столбцу (по потребностям).

Целевая функция Z выражает суммарные расходы на транспортировку грузов. Ограничения по запасам и по потребностям означают, что сумма ресурса, забираемого из /-го источника, должна быть равна запасу ресурса в нем, как и сумма ресурса, доставляемого j-му потребителю, должна быть равна его потребности.

Величина C# может выражать транспортные расходы (минимизация) или прибыль от транспортных операций (максимизация) и другие показатели.

Пример землеустроительной задачи, решаемой транспортным методом. При землеустроительном обследовании в хозяйстве выделено 5 участков с различным плодородием, которые пригодны для трансформирования. Площади участков 250, 100, 520, 310 и 130 га. По проекту на них намечается разместить кормовой севооборот площадью 600 га, полевой — 560 га, улучшенные сенокосы — 150 га. Необходимо распределить севообороты и угодья по участкам так, чтобы получить максимальный чистый доход.

Матрицу исходных данных строим как в табл. 8.1.

Исходные данные для землеустроительной задачи

Чистый доход при размещении на участке, руб/га (Су)

Источник

Модели линейного программирования

Составной частью математического программирования является линейное программирование. Впервые постановка задачи линейного программирования, в виде предложения по составлению оптимального плана перевозок, позволяющего минимизировать суммарный километраж, дана в работе советского ученого экономиста А.Н.Толстого в 1930 году.

Систематическое исследование задач линейного программирования и разработка общих методов их решения начата в работах советского ученого Л.В. Канторович (1939 г.), который предложил общий метод решения этих задач. Он же совместно с М.К.Гавуриным разработал метод потенциалов, который применяется при решении транспортных задач (1949 г.)

Методам линейного программирования посвящено много работ зарубежных, и прежде всего американских ученых.

Основной метод решения задач линейного программирования (симплекс метод) был опубликован в 1949 году Данцигом.

В настоящее время методы линейного программирования развиваются главным образом в направлении выявления конкретных экономических задач, к решению которых оно может быть применено, а также по пути создания более удобных алгоритмов для решения задач на ЭВМ.

Линейное программирование – это наука о методах исследования и отыскания наибольших и наименьших значений линейной функции, на неизвестные которой наложены линейные ограничения

Если система ограничений задачи линейного программирования включает неравенство и уравнение, то задача называется общей задачей линейного программирования, а если только уравнение – то основной задачи линейного программирования (ОЗЛП).

Основная задача линейного программирования заключается в следующем:

Найти неотрицательное значение переменных х₁, х₂, …, х_n, удовлетворяющих “m” условиям — равенства:

и обращающих в max(min) целевую функцию:

Если отыскивается мах функции, то задача линейного программирования называется задачей максимизации, а если min, то задачей минимизации

Задача минимизации легко сводится к задачи максимизации путем замены знаков коэффициентов целевой функции на противоположные.

Допустимым решением основной задачи линейного программирования называют всякую совокупность неотрицательных значений х₁, х₂, x_n, удовлетворяющих системе ограничений.

Оптимальным называют то из допустимых решений, которое обращает в max(min) целевую функцию.

Всякая общая задача линейного программирования может быть сведена к равносильной ей основной задаче путем введения новых неизвестных, называемых дополнительными неизвестные. Переменные, которые входят в ограничения исходной задачи, называется основными

В неравенствах типа «=» из левых частей неравенств вычитаются дополнительные переменные.

Число дополнительных переменных равно числу ограничений — неравенств.

В целевую функцию все дополнительные переменные входят с нулевыми коэффициентами.

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:

Источник

8.2. Распределительная модель линейного программирования

Распределительный метод среди задач линейного программирования получил распространение из-за упрощения расчетов, точности вычислений и снижения затрат времени на ввод исходной информации. Метод предложили А. Толстой и Л. В. Конторович в 1939 – 40 гг. Первоначально он применялся в задачах, связанных с транспортировкой грузов, их распределением между поставщиком и потребителем, поэтому получил название «транспортная задача». Применяется при решении ряда землеустроительных задач: распределение севооборотов и угодий по участкам, размещение культур на землях различных категорий, перераспределение участков между хозяйствами для экономии транспортных затрат и др.

Суть распределительной задачи следующая. Заданы m источников ресурса (производители продукции, базы с готовой продукцией) и n пунктов его потребления. Запасы ресурса в источниках составляют А_i, i=1,…, m, потребности – B_j, j=1,…, n. Стоимость транспортировки единицы ресурса от i-го источника к j-му потребителю С_ij. Количество ресурса, транспортируемого от i-го источника к j-му потребителю Х_ij. Требуется определить такие значения Х_ij, при которых общие транспортные расходы будут минимальны.

При сбалансированности, когда общий спрос на запас ресурса у поставщиков и общий спрос на него у потребителя равны, задачу называют закрытой:

. (8.3)

Если баланс не выдерживается, то транспортная задача является открытой:

, или . (8.4)

При наличии баланса модель транспортной задачи формулируется следующим образом.

(8.5)

Условия. Ограничения по запасам:

(8.6)

Ограничения по потребностям:

(8.7)

(8.8)

X_ij ≥ 0, i = 1,…,m, j = 1,…,n. (8.9)

Особенности распределительных транспортных задач следующие:

• условия задачи описываются уравнениями (в симплекс-методе описываются и неравенствами);
• все переменные выражаются в одних и тех же единицах измерения;
• во всех уравнениях коэффициенты при переменных равны единице;
• каждая переменная встречается только в двух уравнениях системы ограничений: в одном по строке (по запасам) и в одном по столбцу (по потребностям).

Источник