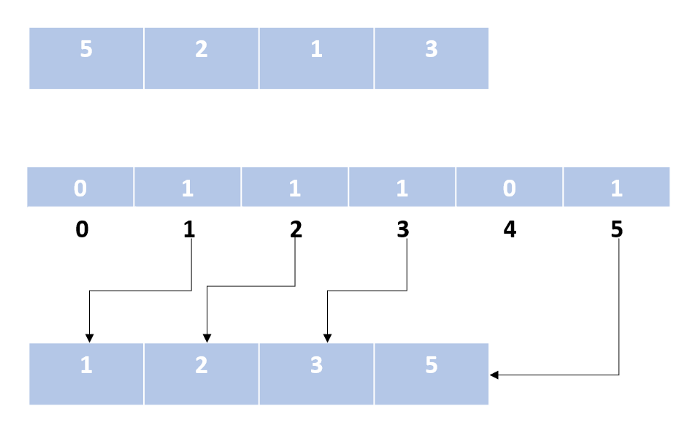
Сортировка выбором максимального элемента питон

Сортировка выбором

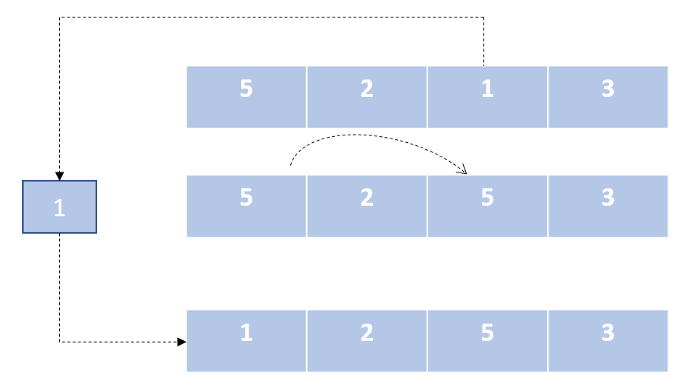
Алгоритм сортировки выбором заключается в поиске на необработанном срезе массива или списка минимального значения и в дальнейшем обмене этого значения с первым элементом необработанного среза (поиск минимума и перестановка). На следующем шаге необработанный срез уменьшается на один элемент.

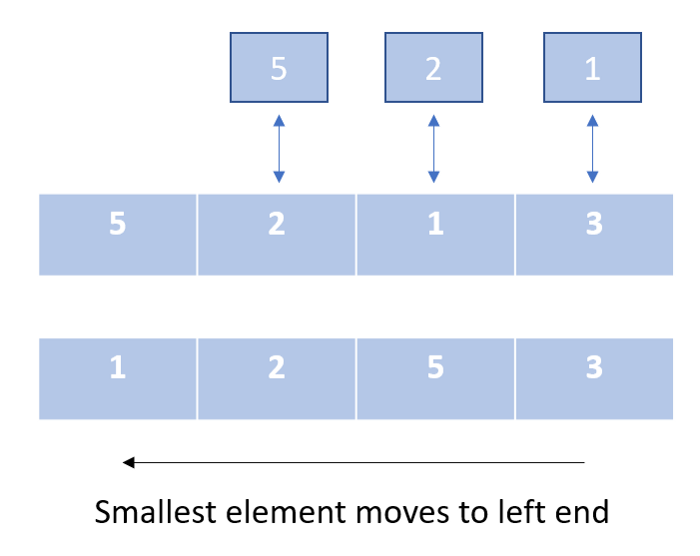
1. Найти наименьшее значение в списке.
2. Записать его в начало списка, а первый элемент — на место, где раньше стоял наименьший.
3. Снова найти наименьший элемент в списке. При этом в поиске не участвует первый элемент.
4. Второй минимум поместить на второе место списка. Второй элемент при этом перемещается на освободившееся место.
5. Продолжать выполнять поиcк и обмен, пока не будет достигнут конец списка.

Решение задачи на языке программирования Python:

# Заполняем список из 10 элементов # случайными числами от 1 до 99 и # выводим неотсортированный список на экран. from random import randint N = 10 arr = [] for i in range(N): arr.append(randint(1, 99)) print(arr) # В цикле переменная i хранит индекс ячейки, # в которую записывается минимальный элемент. # Сначала это будет первая ячейка. i = 0 # N - 1, так как последний элемент # обменивать уже не надо. while i  N - 1: # ПОИСК МИНИМУМА # Сначала надо найти минимальное значение # на срезе от i до конца списка. # Переменная m будет хранить индекс ячейки # с минимальным значением. # Сначала предполагаем, что # в ячейке i содержится минимальный элемент. m = i # Поиск начинаем с ячейки следующей за i. j = i + 1 # Пока не дойдем до конца списка, while j  N: # будем сравнивать значение ячейки j, # со значением ячейки m. if arr[j]  arr[m]: # Если в j значение меньше, чем в m, # сохраним в m номер найденного # на данный момент минимума. m = j # Перейдем к следующей ячейке. j += 1 # ОБМЕН ЗНАЧЕНИЙ # В ячейку i записывается найденный минимум, # а значение из ячейки i переносится # на старое место минимума. arr[i], arr[m] = arr[m], arr[i] # ПЕРЕХОД К СЛЕДУЮЩЕЙ НЕОБРАБОТАННОЙ ЯЧЕЙКЕ i += 1 # Вывод отсортированного списка print(arr)

[77, 46, 11, 89, 48, 14, 67, 73, 22, 26] [11, 14, 22, 26, 46, 48, 67, 73, 77, 89]

Сортировка выбором с помощью цикла for и помещения реализации алгоритма в функцию:

from random import randint N = 10 def sel_sort(row): n = len(row) for i in range(n-1): m = i for j in range(i+1, n): if row[j]  row[m]: m = j row[i], row[m] = row[m], row[i] arr = [randint(1, 99) for item in range(N)] print(arr) sel_sort(arr) print(arr)

Источник

Алгоритмы сортировки на Python

В этой статье мы вкратце расскажем, какие есть основные алгоритмы сортировки и каковы их главные характеристики. Также по каждому алгоритму покажем реализацию на Python.

Искусство наведения порядка

Сортировка означает размещение элементов в определенном порядке. Этот конкретный порядок определяется свойством сравнения элементов. В случае целых чисел мы говорим, что сначала идет меньшее число, а потом — большее.

Расположение элементов в определенном порядке улучшает поиск элемента. Следовательно, сортировка широко используется в информатике.

В данной статье мы рассмотрим обычные алгоритмы сортировки и их реализации на Python. Для сравнения их производительности мы будем рассматривать задачу с сайта Leetcode о сортировке массива. Размеры данных этой задачи ограничены следующим образом:

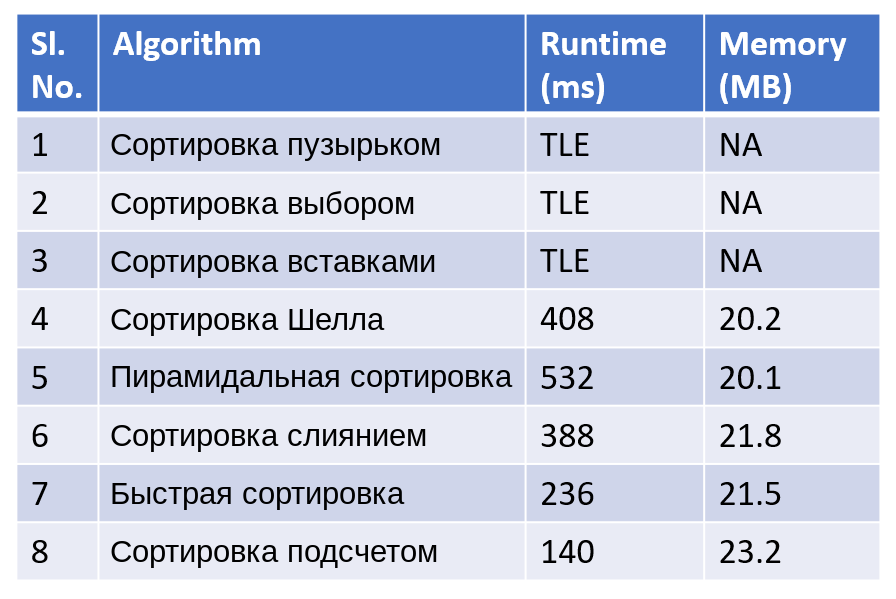
Мы решили эту задачу при помощи всех известных алгоритмов сортировки. Вот какие у нас получились результаты:

Сортировка методом пузырька

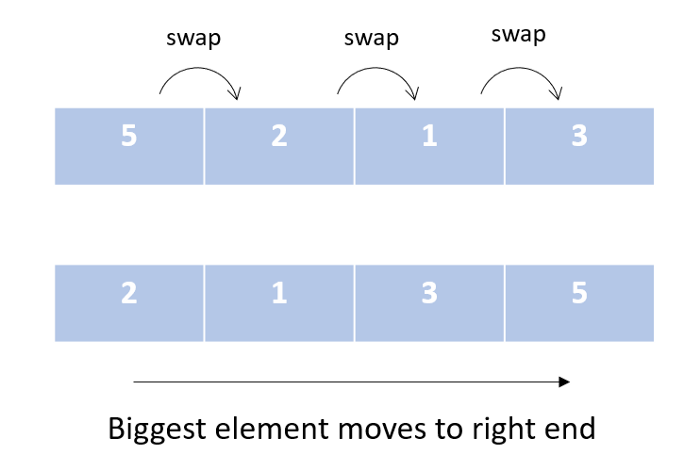
Это самый простой алгоритм сортировки. В процессе его выполнения мы перебираем наш список и на каждой итерации сравниваем элементы попарно. При необходимости элементы меняются местами, чтобы больший элемент отправлялся в конец списка.

• нерекурсивный;
• устойчивый;
• преобразует входные данные без использования вспомогательной структуры данных (in place);
• имеет сложность O(n 2 );

def bubbleSort(array): swapped = False for i in range(len(array)-1,0,-1): for j in range(i): if array[j]>array[j+1]: array[j], array[j+1] = array[j+1], array[j] swapped= True if swapped: swapped=False else: break return array

Сортировка выбором

В этом алгоритме мы создаем два сегмента нашего списка: один отсортированный, а другой несортированный.

В процессе выполнения алгоритма мы каждый раз удаляем самый маленький элемент из несортированного сегмента списка и добавляем его в отсортированный сегмент. Мы не меняем местами промежуточные элементы. Следовательно, этот алгоритм сортирует массив с минимальным количеством перестановок.

• нерекурсивный;
• может быть как устойчивым, так и неустойчивым;
• преобразует входные данные без использования вспомогательной структуры данных (in place);
• имеет сложность O(n 2 );

def selectionSort(array): for i in range(len(array)-1): min_idx = i for idx in range(i + 1, len(array)-1): if array[idx] < array[min_idx]: min_idx = idx array[i], array[min_idx] = array[min_idx], array[i] return array

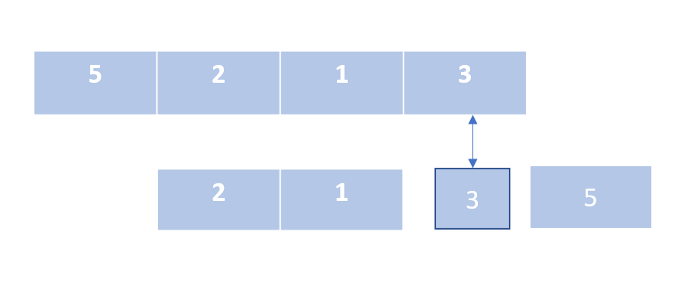
Сортировка вставками

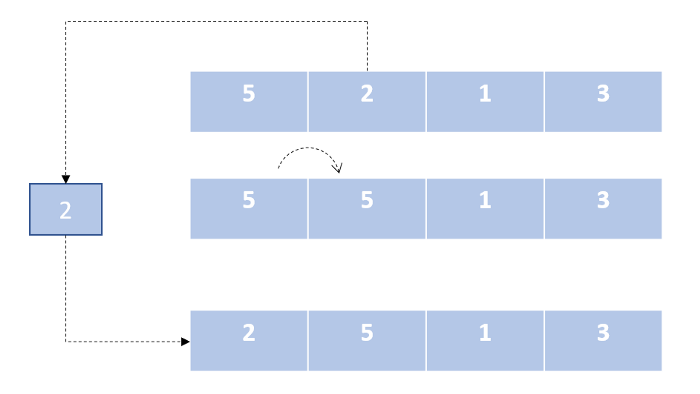
Подобно алгоритму сортировки выбором, мы делим наш список на две части. Далее мы перебираем неотсортированную часть и вставляем каждый элемент из данного сегмента на его правильное место в отсортированной части списка.

• нерекурсивный;
• устойчивый;
• преобразует входные данные без использования вспомогательной структуры данных (in place);
• имеет сложность O(n 2 );

def insertionSort(array): for i in range(1, len(array)): key = array[i] j = i-1 while array[j] > key and j >= 0: array[j+1] = array[j] j -= 1 array[j+1] = key return array

Сортировка Шелла

Сортировка Шелла является оптимизированным вариантом сортировки вставками.

Оптимизация достигается путем сравнения не только соседних элементов, но и элементов на определенном расстоянии, которое в течении работы алгоритма уменьшается. На последней итерации это расстояние равно 1. После этого алгоритм становится обычным алгоритмом сортировки вставками, что гарантирует правильный результат сортировки.

Но следует отметить один момент: к тому времени, когда это произойдет, наш массив будет почти отсортирован, поэтому итерации будут выполнятся очень быстро.

• нерекурсивный;
• устойчивый;
• преобразует входные данные без использования вспомогательной структуры данных (in place);
• имеет сложность O(n 2 ), но это также зависит от выбора длины интервала;

def shellSort(array): n = len(array) k = int(math.log2(n)) interval = 2**k -1 while interval > 0: for i in range(interval, n): temp = array[i] j = i while j >= interval and array[j - interval] > temp: array[j] = array[j - interval] j -= interval array[j] = temp k -= 1 interval = 2**k -1 return array

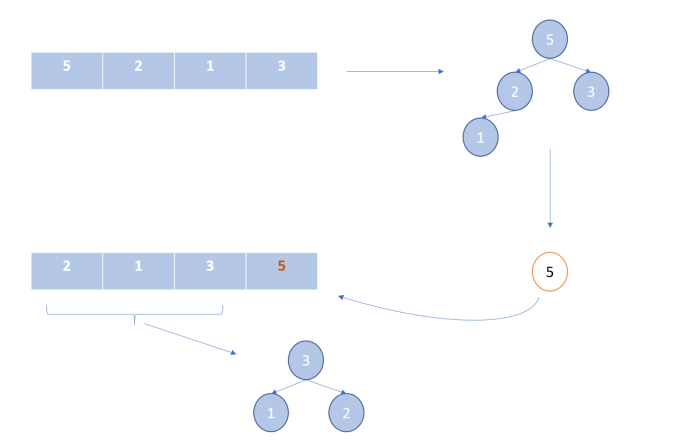
Пирамидальная сортировка («сортировка кучей»)

Как и в двух предыдущих алгоритмах, мы создаем два сегмента списка: отсортированный и несортированный.

В данном алгоритме для эффективного нахождения максимального элемента в неотсортированной части списка мы используем структуру данных «куча».

Метод heapify в примере кода использует рекурсию для получения элемента с максимальным значением на вершине.

• нерекурсивный;
• неустойчивый;
• преобразует входные данные без использования вспомогательной структуры данных (in place);
• имеет сложность O(nlog(n));

def heapify(array, n, i): largest = i l = 2 * i + 1 r = 2 * i + 2 if l < n and array[i] < array[l]: largest = l if r < n and array[largest] < array[r]: largest = r if largest != i: array[i], array[largest] = array[largest], array[i] heapify(array, n, largest) def heapSort(array): n = len(array) for i in range(n//2, -1, -1): heapify(array, n, i) for i in range(n-1, 0, -1): array[i], array[0] = array[0], array[i] heapify(array, i, 0) return array

Сортировка слиянием

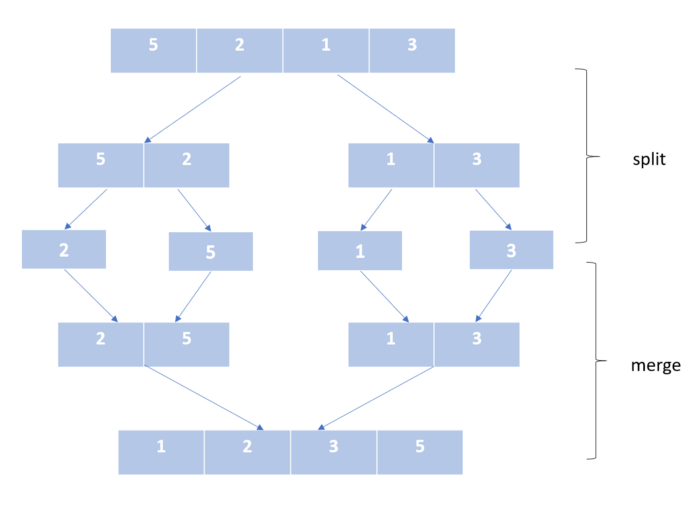
Этот алгоритм работает по принципу «разделяй и властвуй».

Здесь мы делим список ровно пополам и продолжаем это делать, пока в нем не останется только один элемент. Затем мы объединяем уже упорядоченные части нашего списка. Мы продолжаем это делать, пока не получим отсортированный список со всеми элементами несортированного входного списка.

• рекурсивный;
• устойчивый;
• требует дополнительной памяти;
• имеет сложность O(nlog(n));

def mergeSort(nums): if len(nums)==1: return nums mid = (len(nums)-1) // 2 lst1 = mergeSort(nums[:mid+1]) lst2 = mergeSort(nums[mid+1:]) result = merge(lst1, lst2) return result def merge(lst1, lst2): lst = [] i = 0 j = 0 while(ilen(lst1)-1: while(j<=len(lst2)-1): lst.append(lst2[j]) j+=1 else: while(i<=len(lst1)-1): lst.append(lst1[i]) i+=1 return lst

Быстрая сортировка

В этом алгоритме мы разбиваем список при помощи опорного элемента, сортируя значения вокруг него.

В нашей реализации мы выбрали опорным элементом последний элемент массива. Наилучшая производительность достигается тогда, когда опорный элемент делит список примерно пополам.

• рекурсивный;
• неустойчивый;
• преобразует входные данные без использования вспомогательной структуры данных (in place);
• имеет сложность O(nlog(n));

def quickSort(array): if len(array)> 1: pivot=array.pop() grtr_lst, equal_lst, smlr_lst = [], [pivot], [] for item in array: if item == pivot: equal_lst.append(item) elif item > pivot: grtr_lst.append(item) else: smlr_lst.append(item) return (quickSort(smlr_lst) + equal_lst + quickSort(grtr_lst)) else: return array

Сортировка подсчетом

Этот алгоритм не производит сравнение элементов. Для сортировки используются математические свойства целых чисел. Мы подсчитываем вхождения числа в массиве и сохраняем результат во вспомогательном массиве, где индексу соответствует значение ключа.

• нерекурсивный;
• устойчивый;
• преобразует входные данные без использования вспомогательной структуры данных (in place), но все же требует дополнительной памяти;
• имеет сложность O(n);

def sortArray(self, nums: List[int]) -> List[int]: i_lower_bound , upper_bound = min(nums), max(nums) lower_bound = i_lower_bound if i_lower_bound < 0: lb = abs(i_lower_bound) nums = [item + lb for item in nums] lower_bound , upper_bound = min(nums), max(nums) counter_nums = [0]*(upper_bound-lower_bound+1) for item in nums: counter_nums[item-lower_bound] += 1 pos = 0 for idx, item in enumerate(counter_nums): num = idx + lower_bound for i in range(item): nums[pos] = num pos += 1 if i_lower_bound < 0: lb = abs(i_lower_bound) nums = [item - lb for item in nums] return nums

Следует также упомянуть поразрядную сортировку, которая использует сортировку подсчетом либо блочную (корзинную) сортировку в качестве подпрограммы. Этот метод сортировки заслуживает отдельной статьи для разбора.

Для удобства соберем весь наш код вместе:

class Solution: def sortArray(self, nums: List[int]) -> List[int]: # Сортировка пузырьком def bubbleSort(array): swapped = False for i in range(len(array)-1,0,-1): for j in range(i): if array[j]>array[j+1]: array[j], array[j+1] = array[j+1], array[j] swapped= True if swapped: swapped=False else: break return array # Сортировка вставками def insertionSort(array): for i in range(1, len(array)): key = array[i] j = i-1 while array[j] > key and j >= 0: array[j+1] = array[j] j -= 1 array[j+1] = key return array # Сортировка выбором def selectionSort(array): for i in range(len(array)-1): min_idx = i for idx in range(i + 1, len(array)-1): if array[idx] < array[min_idx]: min_idx = idx array[i], array[min_idx] = array[min_idx], array[i] return array # Пирамидальная сортировка def heapify(array, n, i): largest = i l = 2 * i + 1 r = 2 * i + 2 if l < n and array[i] < array[l]: largest = l if r < n and array[largest] < array[r]: largest = r if largest != i: array[i], array[largest] = array[largest], array[i] heapify(array, n, largest) def heapSort(array): n = len(array) for i in range(n//2, -1, -1): heapify(array, n, i) for i in range(n-1, 0, -1): array[i], array[0] = array[0], array[i] heapify(array, i, 0) return array # Сортировка слиянием def mergeSort(nums): if len(nums)==1: return nums mid = (len(nums)-1) // 2 lst1 = mergeSort(nums[:mid+1]) lst2 = mergeSort(nums[mid+1:]) result = merge(lst1, lst2) return result def merge(lst1, lst2): lst = [] i = 0 j = 0 while(ilen(lst1)-1: while(j <=len(lst2)-1): lst.append(lst2[j]) j+=1 else: while(i<=len(lst1)-1): lst.append(lst1[i]) i+=1 return lst # Быстрая сортировка def quickSort(array): if len(array)>1: pivot=array.pop() grtr_lst, equal_lst, smlr_lst = [], [pivot], [] for item in array: if item == pivot: equal_lst.append(item) elif item > pivot: grtr_lst.append(item) else: smlr_lst.append(item) return (quickSort(smlr_lst) + equal_lst + quickSort(grtr_lst)) else: return array # Сортировка Шелла def shellSort(array): n = len(array) interval = n // 2 while interval > 0: for i in range(interval, n): temp = array[i] j = i while j >= interval and array[j - interval] > temp: array[j] = array[j - interval] j -= interval array[j] = temp interval //= 2 return array #nums = bubbleSort(nums) #nums = insertionSort(nums) #nums = selectionSort(nums) #nums = heapSort(nums) #nums = mergeSort(nums) #nums = quickSort(nums) return nums

Испытав все эти алгоритмы, мы ради любопытства запустили встроенную в Python функцию sorted() . Она показала весьма быстрое время в 152 мс. В данной функции используется алгоритм Timsort, который сочетает в себе сортировку слиянием и сортировку вставками. Реализация данного алгоритма также может быть рассмотрена в отдельной статье.

Мы нашли потрясающий плейлист, в котором алгоритмы сортировки демонстрируются при помощи народного танца. Посмотрите это видео, оно того стоит!

Источник