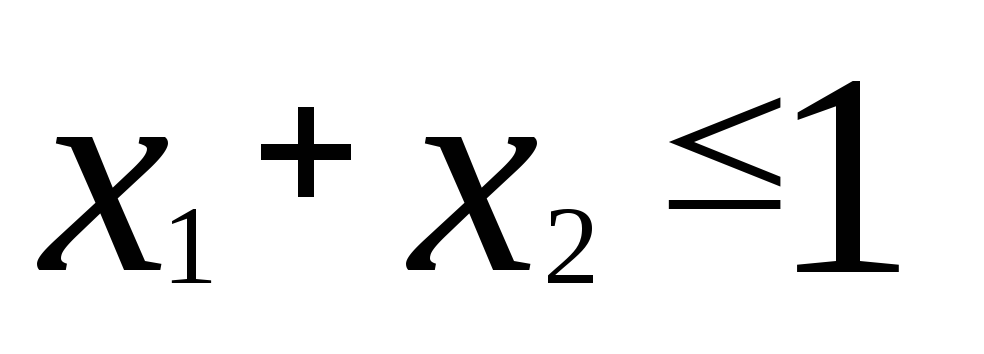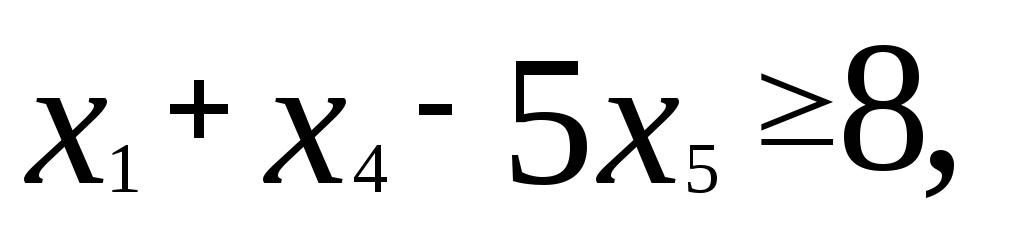Смысл дополнительных переменных задачи линейного программирования

2.Постановка задачи линейного программирования.

Итак, повторим, что необходимо для составление математической модели:

• выбор целевой функции
• выбор переменных задачи
• составление системы ограничений

Целевой функцией задачи называют функцию переменных задачи, которая характеризует качество выполнения задачи, и экстремум которой требуется найти. Переменными задачи называются величины x₁, x₂, x_n, которые полностью характеризуют экономический процесс. Системой ограничений задачи называют совокупность уравнений и неравенств, описывающих ограниченность ресурсов в рассматриваемой задаче. В общем случае задача линейного программирования может быть записана в таком виде: 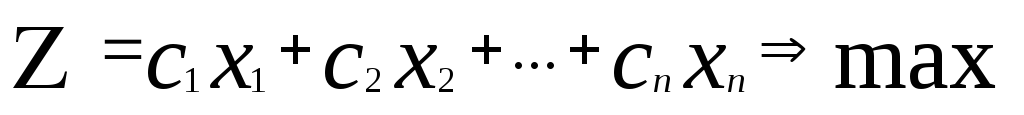(1) a₁₁x₁+a₁₂x₂+…+a_1nx_n ≤ b₁ a₂₁x₁+a₂₂x₂+…+a_2nx_n ≤ b₂ … … …. …. …. ….. …. (2) a_m1x₁+a_m2x₂+…+a_mnx_n ≤ b_m x_j≥0 (j=1,2,…,n), (3) где — заданные постоянные величины, а m>n. Необходимо найти экстремум целевой функции (1) и соответствующие ему переменные x₁, x₂. x_n, при условии, что эти переменные удовлетворяют системе ограничений (2) и условиям неотрицательности (3). Допустимым планом(решением) называется набор значений неизвестных х₁, х₂, …, х_j,…x_n, которые удовлетворяют ее системе ограничений (2) и (3). Множество допустимых решений (планов) задачи образует область допустимых решений (ОДР). Оптимальным решением (планом) задачи линейного программирования называется такое допустимое решение (план) задачи, при котором целевая функция достигает экстремума.

3.Различные формы записи моделей лп. Пример составления математической модели: Задача использования ресурсов (сырья).

Постановка задачи(условие): Для изготовления n видов продукции используется m видов ресурсов 1 . Составить математическую модель. Известны:

• b_i ( i = 1,2,3. m) — запасы каждого i-го вида ресурса;
• a_ij ( i = 1,2,3. m; j=1,2,3. n) — затраты каждого i-го вида ресурса на производство единицы объема j-го вида продукции; a_ij –технологический коэффициент;
• c_j ( j = 1,2,3. n) — прибыль от реализации единицы объема j-го вида продукции.

Требуется составить план производства продукции, который обеспечивает максимум прибыли при заданных ограничениях на ресурсы (сырье). Решение: Введем вектор переменных X=(X₁, X₂. X_j,…,X_n), где x_j ( j = 1,2. n) — объем производства j-го вида продукции. Комментарий: переменные x₁…x_n как мы знаем, являются параметром управления, в данной задаче — это пока неизвестный объём выпускаемой продукции j-го вида. Затраты i-го вида ресурса на изготовление данного объема x_j продукции равны a_ijx_j, поэтому ограничение на использование ресурсов на производство всех видов продукции имеет вид: . Прибыль от реализации j-го вида продукции равна c_jx_j , поэтому целевая функция равна: . Ответ: Математическая модель имеет вид: (4) a₁₁x₁+a₁₂x₂+…+a_1nx_n ≤ b₁ a₂₁x₁+a₂₂x₂+…+a_2nx_n ≤ b₂ … … …. …. …. ….. …. (5) a_m1x₁+a_m2x₂+…+a_mnx_n ≤ b_m x_j≥0 (j=1,2,…,n) (6) Комментарий: (a₁₁,a₁₂,…,a_1n) — использование 1-го вида ресурса на производство всех видов продукции; (a₂₁,a_22,…,a_2n) — использование 2-го вида ресурса на производство всех видов продукции, и т.д. Структурные ограничения (5) отражают требования, которые накладываются на значения переменных (x₁, x₂. x_n) в данном случае — это лимит ресурсов. Если все ограничивающие условия задачи сформулированы в виде неравенств, то говорят, что модель задачи записана в стандартной форме. Запишем эту же мат.модель с помощью знаков суммирования: (7) ) (8) ) (9) В общем случае задача линейного программирования записывается так, что ограничениями являются как уравнения, так и неравенства, а переменные должны быть неотрицательными. В том случае, когда все ограничения являются уравнениями и все переменные удовлетворяют условию неотрицательности, то говорят, что (ЗЛП) задана в канонической форме. Общая задача ЛП может быть представлена в координатной,векторнойиматричной форме записи. Задача линейного программирования в координатной форме записи имеет вид: (10) (11) ). (12) Для матричной формы записи введем обозначения:

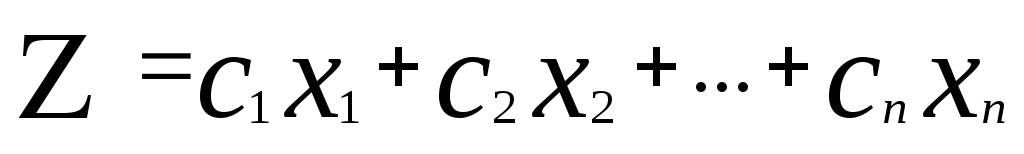
• С — матрица-строка коэффициентов при ЦФ;

• А — матрица коэффициентов системы уравнений;
• Х — матрица-столбец переменных задачи;
• В — матрица-столбец правых частей системы ограничений.

C = (c₁, c₂. c_j,…,c_n); , ,. Таким образом, задача линейного программирования в матричной форме записибудет иметь вид: (13) (14) , (15) Для векторной формы записи введем обозначения: C = (c₁, c₂. c_j,c_n) – n-мерный вектор 2 -строка коэффициентов; ; — n-мерные векторы столбцы; -m-мерные векторы, состоящие из коэффициентов при неизвестных в ограничениях (A_j, j=) и свободных членов (B). Тогда мат. модель общей задачи ЛП может быть записана так: (16) (17) (18) Мы рассмотрели математическую модель общей задачи ЛП на максимум и различные формы ее записи. Задачу максимизации линейной функции всегда можно свести к задаче минимизации той же линейной функции со знаком минус, при этом используется соотношение: maxZ= −min(−Z) (19) Из (19) следует, что для сведения задачи на максимум к задаче на минимум достаточно у коэффициентов ЦФ поменять знаки на противоположные и найти минимум полученной функции (−Z). В экономике при неравенствах вида ≤, как правило, формулируются задачи на максимум, а при неравенствах вида ≥, как правило, формулируются задачи наминимум. Различают следующие формы математических моделей общей задачи ЛП в зависимости от соотношений между правыми и левыми частями ограничивающих условий:

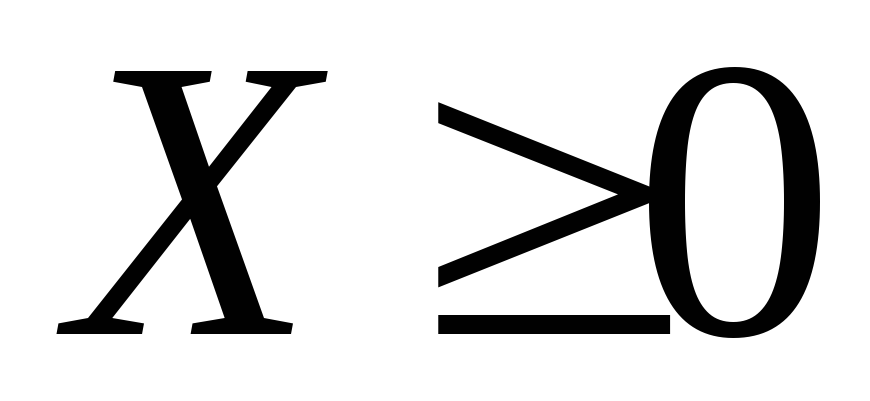
• Модели задач в стандартной форме, когда между левой и правой частями ограничений стоит знак неравенства: (≤) Ц.Ф. задана на max,(≥) Ц.Ф. на min.
• Каноническая форма, когда между левой и правой частями ограничений стоит знак равенства, при такой форме ограничений возможна и максимизация, и минимизация целевой функции.
• Смешанная форма, когда одна часть ограничений представлена в виде равенств, а другая — в виде неравенств

Для приведения моделей задач стандартной формы к канонической достаточно в левую часть ограничений ввести дополнительные переменные: х_п+1, х_п+2,.х_п+m. Эти переменные вводятся со знаком «плюс» если между левой и правой частью ограничений стоит неравенство «≤» или со знаком «минус» если стоит неравенство «≥». Подобным образом можно привести к каноническому виду задачи со смешанной системой ограничивающих условий. Дополнительные переменные необходимо ввести также и в целевую функцию задачи с нулевыми коэффициентами, а также в условия неотрицательности переменных. Число вводимых дополнительных неотрицательных переменных при преобразовании ограничений-неравенств в ограничения-равенства равно числу преобразуемых неравенств. Вводимые дополнительные переменные имеют вполне определенный экономический смысл. Так, если в ограничениях исходной задачи линейного программирования отражается расход и наличие производственных ресурсов, то числовое значение дополнительной переменной в плане задачи, записанной в форме основной, равно объему неиспользуемого соответствующего ресурса. Любую задачу линейного программирования можно свести к задаче линейного программирования в канонической форме. Для этого в общем случае нужно уметь сводить задачу максимизации к задаче минимизации; переходить от ограничений неравенств к ограничениям равенств. Пример 1 . Привести задачу к канонической форме записи: Введем дополнительные переменные ,по количеству существующих неравенств в ограничения со знаком (+), а также в ЦФ с нулевыми коэффициентами и в условие неотрицательности переменных: ,что и дает нам задачу в канонической форме. Пример 2. Привести задачу к канонической форме записи: при (ограничениях): , ,

Источник

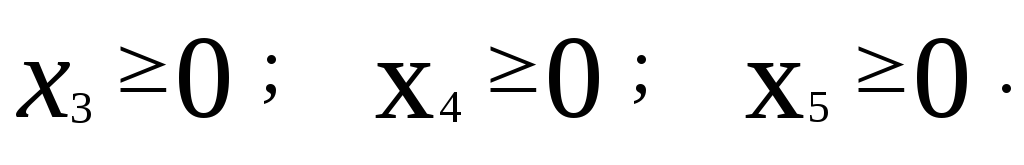
Виды злп и способы перехода от одного вида к другому.

Одна и та же ЗЛП может быть сформулирована в различных эквивалентных формах. Наиболее важными формами задачи линейного программирования являются каноническая и стандартная.

В канонической форме задача является задачей на максимум (минимум) некоторой линейной функции F, ее система ограничений состоит только из равенств (уравнений). При этом переменные задачи х₁, х₂, . х_n являются неотрицательными:

К канонической форме можно преобразовать любую задачу линейного программирования.

Правило приведения ЗЛП к каноническому виду:

1. Если в исходной задаче некоторое ограничение (например, первое) было неравенством, то оно преобразуется в равенство, введением в левую часть некоторой неотрицательной переменной, при чем в неравенства «≤» вводится дополнительная неотрицательная переменная со знаком «+»; в случаи неравенства «≥» — со знаком «-»

Тогда неравенство (32.1) запишется в виде:

В каждое из неравенств вводится своя “уравнивающая” переменная, после чего система ограничений становится системой уравнений.

Число вводимых дополнительных неотрицательных переменных при преобразовании ограничений-неравенств в ограничения-равенства равно числу преобразуемых неравенств.

Вводимые дополнительные переменные имеют вполне определенный экономический смысл. Так, если в ограничениях исходной задачи линейного программирования отражаются расход и наличие производственных ресурсов, то числовое значение дополнительной переменной в плане задачи, записанной в основной форме, равно объему неиспользуемого соответствующего ресурса.

2. Если в исходной задаче некоторая переменная не подчинена условию неотрицательности, то ее заменяют (в целевой функции и во всех ограничениях) разностью неотрицательных переменных

3. Если в ограничениях правая часть отрицательна, то следует умножить это ограничение на (-1)

4. Наконец, если исходная задача была задачей на минимум, то введением новой целевой функции F₁ = -F мы преобразуем нашу задачу на минимум функции F в задачу на максимум функции F₁.

Таким образом, всякую задачу линейного программирования можно сформулировать в канонической форме.

В стандартной форме задача линейного программирования является задачей на максимум (минимум) линейной целевой функции. Система ограничений ее состоит из одних линейных неравенств типа « = »). Все переменные задачи неотрицательны.

Всякую задачу линейного программирования можно сформулировать в стандартной форме. Приведение к стандартной форме необходимо, так как большинство методов решения задач линейного программирования разработано именно для стандартной формы.

Для приведения к стандартной форме задачи линейного программирования может потребоваться выполнить следующие действия:

— перейти от минимизации целевой функции к ее максимизации;

— изменить знаки правых частей ограничений;

— перейти от ограничений-равенств к неравенствам;

— избавиться от переменных, не имеющих ограничений на знак..

1. Привести к каноническому виду задачу

Введем дополнительные переменные x₃ , x₄ , x₅ . Причем в первое неравенство введем неотрицательную переменную x₃ со знаком минус, а во второе и в третье – со знаком плюс переменные x₄ , x₅ запишем задачу в виде:

что и дает эквивалентную задачу в канонической форме.

2. Привести к стандартному виду задачу

Выразим через и остальные переменные:

Целевая функция будет выглядеть следующим образом:

Так как , то перепишем нашу систему следующим образом: .

Итак, эквивалентная задача в стандартной форме будет выглядеть следующим образом:

Источник