Сложность алгоритма быстрой сортировки равна python

Алгоритм быстрой сортировки — реализация на C++, Java и Python

Дан целочисленный массив, отсортируйте его с помощью алгоритма быстрой сортировки.

Обзор быстрой сортировки

Быстрая сортировка — эффективный алгоритм сортировки на месте, который обычно работает примерно в два-три раза быстрее, чем Сортировка слиянием а также сортировка кучей при хорошей реализации. Быстрая сортировка — это сортировка сравнением, то есть она может сортировать элементы любого типа, для которых меньше, чем отношение определено. В эффективных реализациях это обычно нестабильная сортировка.

Быстрая сортировка в среднем дает O(n.log(n)) сравнения для сортировки n Предметы. В худшем случае получается O(n 2 ) сравнения, хотя такое поведение встречается очень редко.

Как работает быстрая сортировка?

Быстрая сортировка — это Разделяй и властвуй алгоритм. Как и все алгоритмы «разделяй и властвуй», он сначала делит большой массив на два меньших подмассива, а затем рекурсивно сортирует подмассивы. По сути, весь процесс включает три этапа:

• Выбор опоры: Выберите элемент, называемый опорным, из массива (обычно это самый левый или самый правый элемент раздела).
• Разделение: Переупорядочите массив таким образом, чтобы все элементы со значениями меньше опорного располагались перед опорным. Напротив, все элементы со значениями больше, чем точка опоры, идут после нее. Равные значения могут идти в любом направлении. После этого разбиения стержень занимает свое конечное положение.
• Повторять: Рекурсивно примените описанные выше шаги к подмассиву элементов с меньшими значениями, чем у опорного, и отдельно к подмассиву элементов с большими значениями, чем у опорного.

Базовым случаем рекурсии являются массивы размером 1 , которые никогда не нужно сортировать. На следующей диаграмме показано, как мы выбираем крайний левый элемент в качестве опорного на каждом этапе алгоритма быстрой сортировки, разбиваем массив по опорному элементу и повторяемся в двух подмассивах, которые мы получаем после процесса разделения:

Обратите внимание, что этапы выбора опоры и разбиения могут быть выполнены несколькими способами, и выбор конкретных схем реализации существенно влияет на производительность алгоритма. Мы обсудим все это подробно позже, а сейчас давайте перейдем к части кодирования.

Ниже приведена реализация алгоритма Quicksort на C++, Java и Python:

Источник

Визуализация 5 алгоритмов сортировки на Python

Реализация алгоритмов сортировки: выбором, пузырьком, вставками, слиянием и быстрой сортировкой с помощью Python.

Введение

Сортировка массивов часто используется в программировании, чтобы помочь понять данные и выполнить поиск. Поэтому скорость сортировки больших объемов информации крайне важна для функциональных проектов и оптимизации времени работы. Есть много алгоритмов для упорядочения объектов.

В статье вы посмотрите на реализацию и визуализацию пяти популярных алгоритмов сортировки. Код написан на Python, а графический интерфейс построен на Tkinter.

Эти 5 алгоритмов включают:

• Сортировка выбором
• Сортировка пузырьком
• Сортировка вставками
• Сортировка слиянием
• Быстрая сортировка quicksort

Визуализация массива

Как только класс предоставляет перегруженные реализации операторов сравнения, он сортируется. На Python это:

Код ниже демонстрирует перегруженный метод меньше чем.

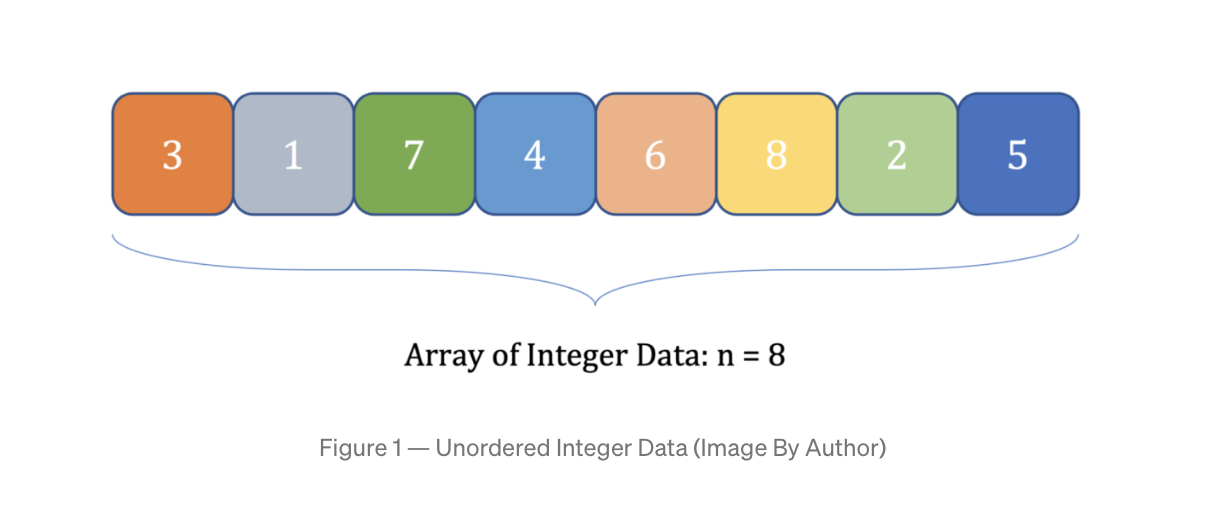
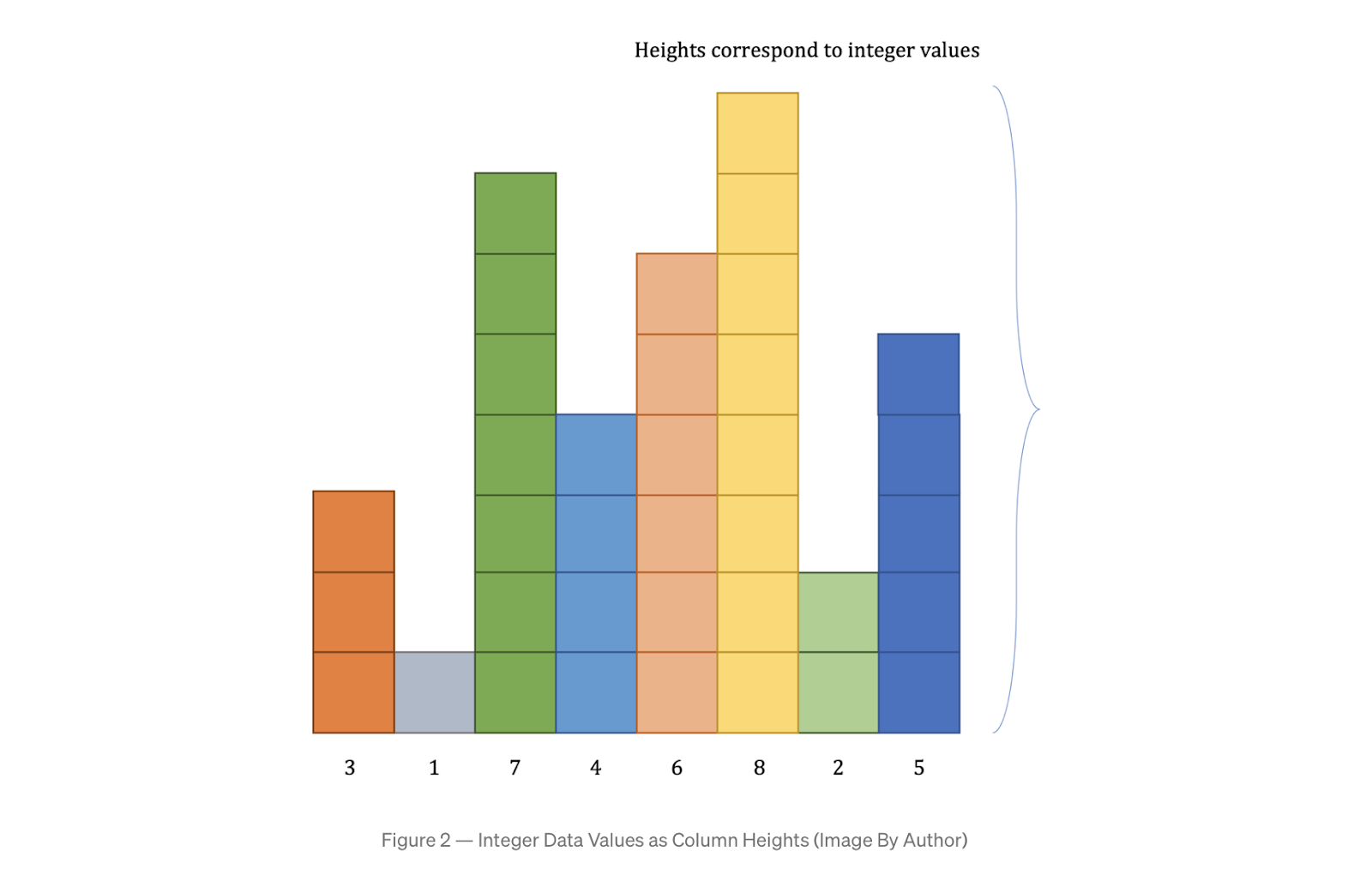
def __lt__(self, other): # compare object with "other" object of same type return self.value < other.value

Давайте представим числовые данные с помощью столбцов. Высота столбца i равна значению элемента массива i. У них всех одинаковая ширина. Такое изображение списка числовых значений с Рис. 1 в виде столбцов приведено на Рис. 2.

Сортировка числовых данных по убыванию или по возрастанию требует соответствующей перестановки значений. Для анимации каждого алгоритма с данными, требуется обновлять диаграмму после замены отдельных элементов.

Ниже — код Python для замены двух элементов в списке.

def swap(arr, a, b): """ переставляем элементы a и b в массиве """ temp = arr[a] arr[a] = arr[b] arr[b] = temp # возвращаем массив

Для рендеринга необходимы два класса: Canvas, и Bar. Код с комментариями для полного пользовательского интерфейса лежит в репозитории GitHub.

Ниже показан необходимый код для отображения обновлений в классе Canvas . Если bar index меняется, как указано выше, setter запускает функцию update_bar на основном холсте. После запуска обновления элементы массива меняются местами.

@index.setter def index(self, i): """ update coordinates when index changes """ self._index = i # update horizontal coordinates self.x1 = self._index * self.width self.x2 = self.x1 + self.width # dispatch updates to subscriber (visualiser) self.subscriber.update_bar(self)

Сортировка выбором

Встроенный алгоритм сортировки, то есть отсортированные элементы используют то же хранилище, что и исходные элементы.

Ниже — реализация сортировки выбором на Python с подробными комментариями.

Внешний цикл производит итерации по всей длине несортированного массива. В это время внутренний цикл ищет минимальное значение в оставшейся части набора данных. Затем происходит единая замена, переставляющая элемент под номером i и элемент min_index .

def selection_sort(self, unsorted, n): # итерируемся по массиву for i in range(0, n): # инициализируемся первым значеним current_min = unsorted[i] # инициализируем минимальный индекс min_index = i # итерируемся по оставшимся элементам массива for j in range(i, n): # проверяем, если j-тое значение меньше текушего минимального if unsorted[j] < current_min: # обновляес минимальные значение и индекс current_min = unsorted[j] min_index = j # меняем i-тое и j-тое значения swap(unsorted, i, min_index)

Метод сортировки выбором обычно включает параметры:

• Временная сложность = O(n²).
  n² итераций очевидны из двух вложенных циклов.
• Пространственная сложность = O(1).
  Как упоминалось выше, сортировка происходит в том же массиве, поэтому использование памяти не зависит от данных обработки.

Сортировка пузырьком

Несколько раз проходит по списку, сравнивая соседние элементы. Элементы меняются местами в зависимости от условия сортировки.

Ниже показана реализация сортировки выбором на Python с комментариями.

def bubble_sort(self, unsorted, n): """ алгоритм сортировки пузырьком """ # итерируемся по неотсорт. массиву до предпоследнего элемента for i in range(0, n - 1): # проставляем условия флага для финального списка swapped = False # итерируемся по осташвимся неотсортированным объектам for j in range(0, n - 1 - i): # сравниваем соседние элементы if unsorted[j].value > unsorted[j + 1].value: # меняем элементы местами swap(unsorted, j, j + 1) swapped = True # завершаем алгоритм, если смены не произошло if not swapped: break

Обратите внимание, что из всех алгоритмов у сортировки пузырьком наихудший случай и среднее значение:

• Временная сложность = O(n²).
  Внутренний цикл работает не менее n раз. Поэтому операция займет не менее n² времени
• Пространственная сложность = O(1).
  Дополнительная память не используется, потому что происходит обмен элементов в исходном массиве

Большие значения всплывают, как пузырьки, в верхнюю часть списка по мере выполнения программы, как показано на Рис. 4.

Сортировка вставками

Строит конечный массив по одному элементу за раз. Используйте код, указанный ниже для выполнения метода над несортированным массивом объектов.

 def insertion_sort(unsorted, n): """ сортировка вставками """ # итерация по неотсортированным массивам for i in range(1, n): # получаем значение элемента val = unsorted[i].value # записываем в hole индекс i hole = i # проходим по массиву в обратную сторону, пока не найдём элемент больше текущего while hole > 0 and unsorted[hole - 1].value > val: # переставляем элементы местами , чтобы получить правильную позицию unsorted[hole].value = unsorted[hole - 1].value # делаем шаг назад hole -= 1 # вставляем значение на верную позицию unsorted[hole].value = val

У сортировки вставками есть наихудший случай:

• Временная сложность = O(n²). Как внешний цикл for, так и внутренний while работают приблизительно n раз
• Пространственная сложность = O(1). Операции проводятся с исходным массивом. Таким образом, дополнительной памяти не требуется.

Сортировка слиянием

Сортировка слиянием — алгоритм сортировки по принципу «разделяй и властвуй». Задача раскладывается на более мелкие аналогичные подзадачи до тех пор, пока не будет решен базовый случай.

Несортированный массив разделяется до тех пор, пока не выделится базовый случай отдельных элементов. Затем происходит сравнение между временными массивами, перемещающимися обратно вверх по стеку рекурсии.

def divide(self, unsorted, lower, upper): """ рекурсивная функция для разделения массива на два подмассива для сортировки """ # с помощью рекурсии достигнут базовый случай if upper 

def quick_sort(self, unsorted, start, end): """ быстрая сортировка """ # останавливаемся, когда индекс слева достиг или превысил индек справа if start >= end: return # определяем позицию следующего пивота i_pivot = partition(unsorted, start, end - 1) # рекурсивный вызов левой части quick_sort(unsorted, start, i_pivot) # рекурсивный вызов правой части quick_sort(unsorted, i_pivot + 1, end) def partition(self, unsorted, start, end): """ arrange (left array < pivot) and (right array >pivot) """ # выбираем значение pivot как последний элемент неотсортированного сегмента pivot = unsorted[end] # назначаем на pivot значение левого индекса i_pivot = start # проходим от начала до конца текущего сегмента for i in range(start, end): # сравниваем текущее значение со значением pivot if unsorted[i].value