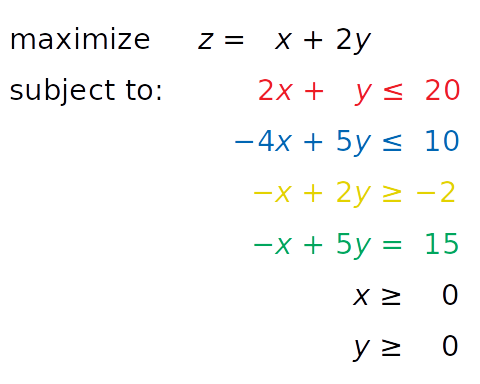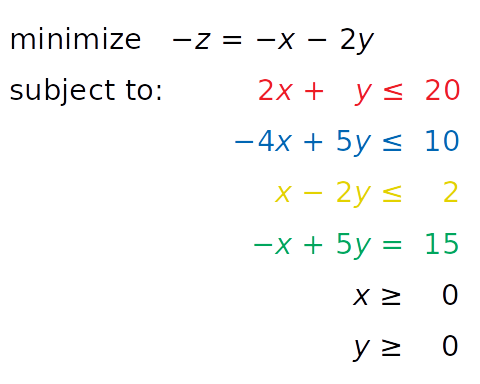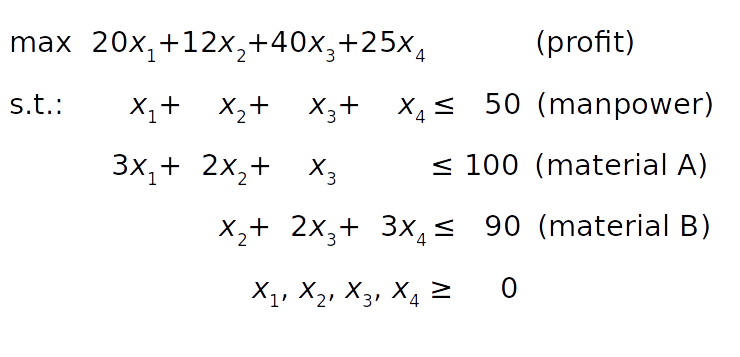Сложная задача линейное программирование

Линейное программирование. Решение задач

Ниже представлены примеры решения задач линейного программирования.

Линейное программирование. Решение задач графическим способом

Симплексный метод решения задач линейного программирования

1. Метод искусственного базиса
2. Задача оптимального производства продукции
3. Пример решения симлекс-методом
   Решить следующую задачу ЛП в неканонической форме симплекс-методом:
   f(x) = x₁ – x₂ – 3x₃ → min
4. М-метод. Решить задачу М-задачу.
5. Пример нахождения максимума функции симплексным методом
6. Пример нахождения минимума функции симплексным методом
7. Пример решения модифицированным симплекс-методом
8. Пример решения симплекс-методом в столбцовой форме записи
9. Симплекс-метод в строчечной форме записи. Пример решения
10. Пример решения задачи симплексным методом в Excel
11. Линейное программирование в Excel

Решение двойственной задачи линейного программирования

1. Двойственная задача ЛП
   Необходимо выполнить в указанном порядке следующие задания.
   1. Найти оптимальный план прямой задачи:
   а) графическим методом;
   б) симплекс-методом (для построения исходного опорного плана рекомендуется использовать метод искусственного базиса).
   2. Построить двойственную задачу.
   3. Найти оптимальный план двойственной задачи из графического решения прямой, используя условия дополняющей нежесткости.
2. Двойственная задача в Excel
3. Оценка целесообразности выпуска новой продукции

Двойственный симплекс-метод

Методы линейного программирования применяются для решения многих экстремальных задач, с которыми довольно часто приходится иметь дело в экономике. Решение таких задач сводится к нахождению крайних значений (максимума и минимума) некоторых функций переменных величин. Линейное программирование основано на решении системы линейных уравнений (с преобразованием в уравнения и неравенства), когда зависимость между изучаемыми явлениями строго функциональна. Для него характерны математическое выражение переменных величин, определенный порядок, последовательность расчетов (алгоритм), логический анализ. Применять его можно только в тех случаях, когда изучаемые переменные величины и факторы имеют математическую определенность и количественную ограниченность, когда в результате известной последовательности расчетов происходит взаимозаменяемость факторов, когда логика в расчетах, математическая логика, совмещаются с логически обоснованным пониманием сущности изучаемого явления. Методом линейного программирования решается транспортная задача, т.е. задача рационального прикрепления предприятий-потребителей к предприятиям-производителям.

Источник

2. Линейное программирование на Python. Практическая реализация

В этом руководстве мы будем использовать для решения описанной выше задачи линейного программирования два пакета Python :

1. SciPy – универсальный пакет для научных вычислений с Python. Его внутренний пакет scipy.optimize можно использовать как для линейной, так и для нелинейной оптимизации.
2. PuLP – API линейного программирования Python для определения задачи и вызова солверов. По умолчанию в качестве солвера используется COIN-OR Branch and Cut Solver (CBC). Еще один отличный солвер с открытым исходным кодом – GNU Linear Programming Kit (GLPK).

2.1. Установка SciPy и PuLP

Чтобы следовать этому руководству, вам необходимо установить SciPy и PuLP.

linprog() решает только задачи минимизации (не максимизации) и не допускает ограничений-неравенств со знаком больше или равно ( ≥ ). Чтобы обойти эти проблемы, нам необходимо изменить описание задачи перед запуском оптимизации:

• Вместо максимизации z = x + 2y минимизируем отрицательное значение ( −z = −x − 2y ).
• Вместо знака ≥ мы можем умножить «желтое» неравенство на -1 и получить противоположный знак (ограничения по осям рассмотрим далее).

На следующем шаге определяем входные значения:

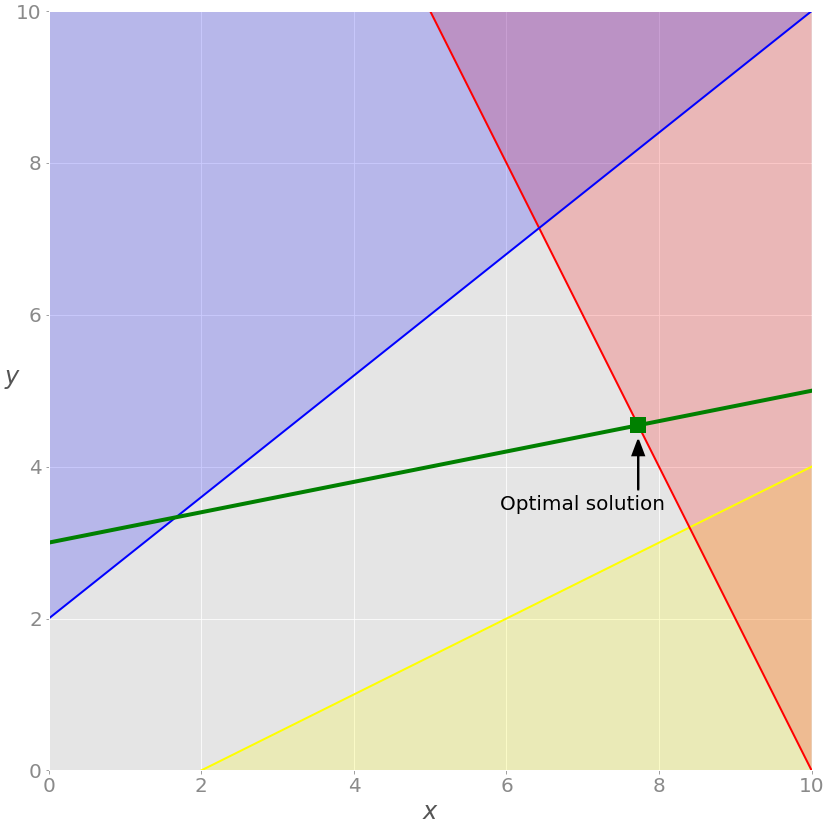
Вначале наша задача органичивалась только неравенствами. Если удалить параметры зеленого уравнения A_eq и b_eq из вызова linprog() , получим следующий результат:

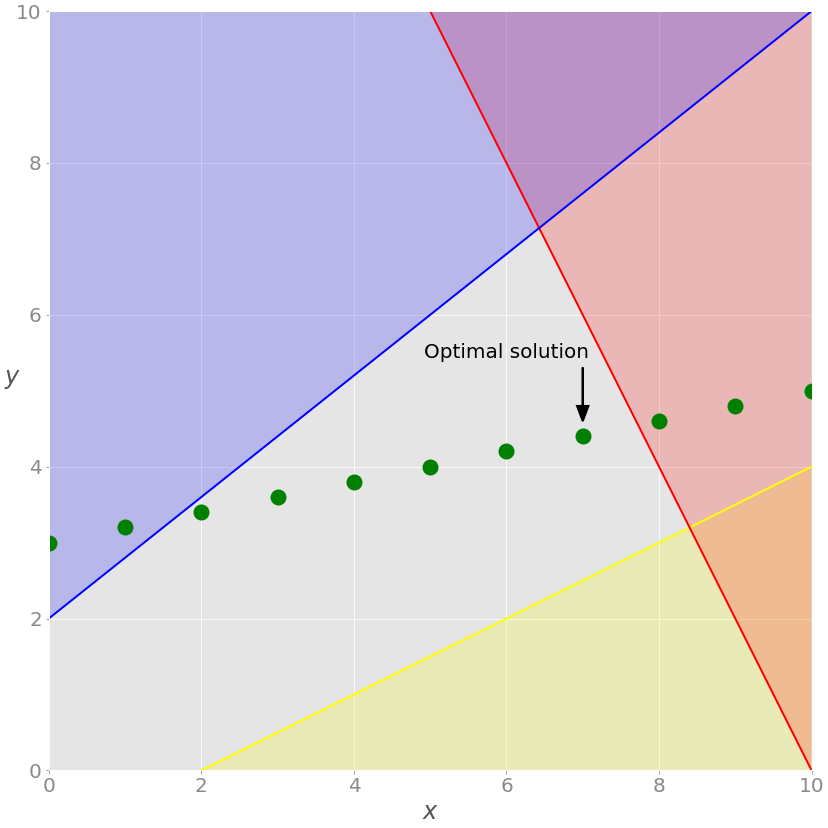
2.4. Решение задачи о производстве с помощью SciPy

Рассмотрим теперь решение второй задачи – о продуктах, рабочей силе и используемом сырье.

Как и в предыдущем примере, нам нужно извлечь необходимые векторы и матрицу из задачи, передать их в качестве аргументов в linprog() :

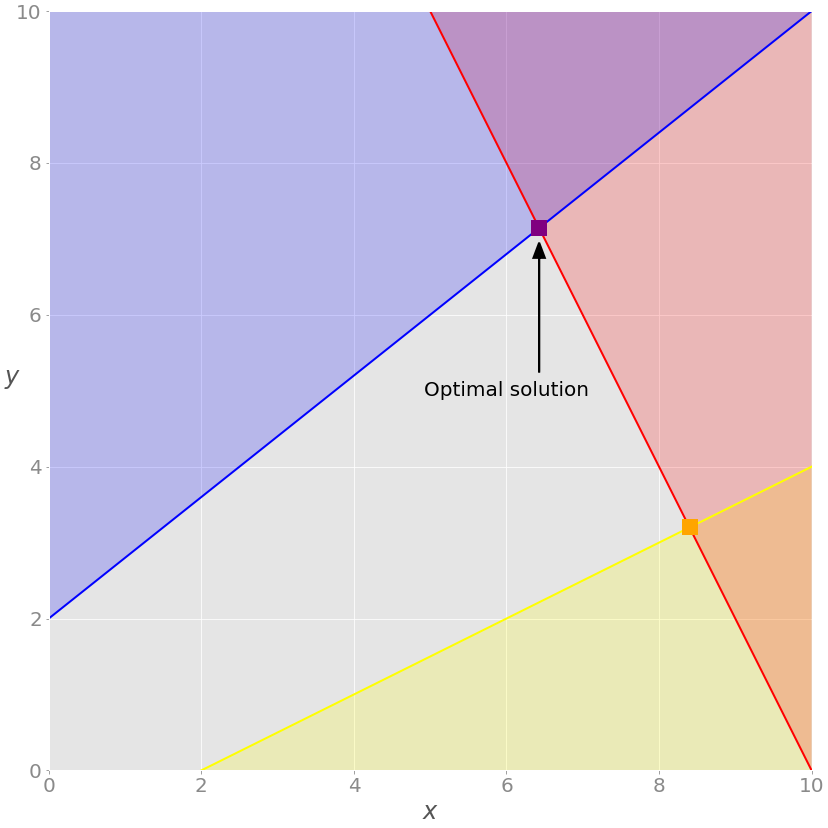
Как видите, оптимальным решением является крайняя правая зеленая точка на сером фоне. Это решение с наибольшими значениями как x , так и y , дающее максимальное значение целевой функции.

2.6. Решение задачи о производстве с помощью PuLP

Подход к определению и решению второй задачи такой же, как и в предыдущем примере:

# Определяем модель model = LpProblem(name="resource-allocation", sense=LpMaximize) # Описываем переменные x = ", lowBound=0) for i in range(1, 5)> # Добавляем ограничения model += (lpSum(x.values()) , ") print(f"objective: ") for var in x.values(): print(f": ") for name, constraint in model.constraints.items(): print(f": ") 

status: 1, Optimal objective: 1900.0 x1: 5.0 x2: 0.0 x3: 45.0 x4: 0.0 manpower: 0.0 material_a: -40.0 material_b: 0.0 

Как видите, решение согласуется с тем, что мы молучили с помощью SciPy. Наиболее выгодное решение – производить в день 5 единиц первого продукта и 45 единиц третьего.

Давайте сделаем задачу более интересной. Допустим, из-за проблем с оборудованием, фабрика не может производить первую и третью продукцию параллельно. Какое решение наиболее выгодно в этом случае?

Теперь у нас есть еще одно логическое ограничение: если x_1 положительно, то x_3 должно равняться нулю, и наоборот. Здесь пригодятся бинарные переменные решения. Введем две переменные y_1 и y_3 , которые будут обозначать, генерируются ли вообще первый или третий продукты:

model = LpProblem(name="resource-allocation", sense=LpMaximize) x = ", lowBound=0) for i in range(1, 5)> y = ", cat="Binary") for i in (1, 3)> model += (lpSum(x.values()) , ") print(f"objective: ") for var in model.variables(): print(f": ") for name, constraint in model.constraints.items(): print(f": ") 

status: 1, Optimal objective: 1800.0 x1: 0.0 x2: 0.0 x3: 45.0 x4: 0.0 y1: 0.0 y3: 1.0 manpower: -5.0 material_a: -55.0 material_b: 0.0 x1_constraint: 0.0 x3_constraint: -55.0 y_constraint: 0.0 

При таких условиях оказывается, что оптимальный подход – исключить первый продукт вовсе и производить только третий.

Заключение

Теперь вы в общих чертах представляете, с какими задачами имеет дело линейное программирование и как использовать Python для решения подобных задач.

Теперь – после прохождения этого руководства – вы умеете:

• определить модель, которая описывает задачу в SciPy и PuLP;
• создать программу Python для оптимизационной задачи;
• запустить программу оптимизации, чтобы найти решение задачи;
• получить результат оптимизации.

Если вы хотите узнать больше о линейном программировании, вот несколько отправных точек, с которых можно начать:

• русскоязычная и анлоязычная вики-страницы о линейном программировании;
• русскоязычная и англоязычная вики-страницы о целочисленном программировании;
• туториал на Brilliant.org;
• вводный курс MIT о математическом программировании.

Следите за нашими тегами Python и Математика!

Больше полезной информации вы можете получить на нашем телеграм-канале «Библиотека питониста». Рекомендуем также обратить внимание на учебный курс по Python от «Библиотеки программиста».

Источники

Источник