Аналитические методы
Аналитическими методами в рассматриваемой классификации названы методы, которые отображают реальные объекты и процессы в виде точек (безразмерных в строгих математических доказательствах), совершающих какие-либо перемещения в пространстве или взаимодействующих между собой.
Основу понятийного (терминологического) аппарата этих представлений составляют понятия классической математики (величина, формула, функция, уравнение, система уравнений, логарифм, дифференциал, интеграл и т.д.).
Для аналитических представлений характерно не только стремление к строгости терминологии, но и закрепление за некоторыми специальными величинами определенных букв (например, удвоенное отношение площади круга к площади вписанного в него квадрата %%\pi\approx 3,14%%; основание натурального логарифма е %%\approx 2,7%% и т.д.).
На базе аналитических представлений возникли и развиваются математические теории различной сложности — от аппарата классического математического анализа до новых разделов современной математики (математическое программирование, теория игр и т.п.). Эти теоретические направления стали основой многих прикладных дисциплин, в том числе теории автоматического управления, теории оптимальных решений и т.д.
При моделировании систем применяется широкий спектр символических представлений, использующих «язык» классической математики. Однако далеко не всегда эти символические представления адекватно отражают реальные сложные процессы, и их в этих случаях, вообще говоря, нельзя считать строгими математическими моделями.
Большинство из направлений математики не содержит средств постановки задачи и доказательства адекватности модели. Адекватность модели доказывается экспериментом, который по мере усложнения проблем становится также все более сложным, дорогостоящим, не всегда бесспорен и реализуем.
В то же время в состав этого класса методов входит относительно новое направление математики — математическое программирование, которое содержит средства постановки задачи и расширяет возможности доказательства адекватности моделей.
Привлекательность методов математического программирования для решения слабо формализованных задач (каковыми, как правило, являются задачи планирования, распределения работ и ресурсов, загрузки оборудования и другие задачи управления современным предприятием на начальном этапе их постановки) объясняется рядом особенностей, отличающих эти методы от методов классической математики.
Для пояснения этих особенностей рассмотрим упрощенный пример.
Предположим, что в трех цехах (Ц1, Ц2, Ц3) изготавливается два вида изделий И1 и И2. Известна загрузка каждого цеха %%a_i%% (оцениваемая в данном случае в про центах) при изготовлении каждого из изделий и прибыль (или цена, объем реализуемой продукции в рублях) %%c_i%% от реализации изделий. Требуется определить, сколько изделий каждого вида следует производить при возможно более полной загрузке цехов, чтобы получить за рассматриваемый плановый период максимальную прибыль или максимальный объем реализуемой продукции.
Такую ситуацию удобно отобразить в виде таблицы (табл. 2.1), которая подсказывает характерную для задач математического программирования форму представления задачи, т.е. целевую функцию (в данном случае определяющую максимизацию прибыли или объема реализуемой продукции).
$$F=\sum_^c_ix_i=240x_i+320x_2→max,$$и ряд ограничений (в данном случае диктуемых возможностями цехов, т.е. их предельной 100%-ной загрузкой)
В данном случае ограничения однородны и их можно записать короче:
| Изделия | Ц1 | Ц2 | Ц3 | Цена изделия, руб. |
|---|---|---|---|---|
| И1 | 5 | 1,6 | 2,9 | 240 |
| И2 | 4 | 6,4 | 5,8 | 320 |
| Максимальная загрузка, % | 100 | 100 | 100 | — |
 |
|---|
| Рис. 2.4 |
В общем случае может быть несколько групп подобных ограничений (например, по имеющимся материалам разного вида, себестоимости, заработной пдате рабочих и т.п.).
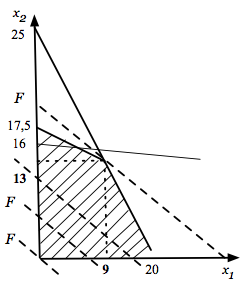
Графическое решение задачи приведено на рис. 2.4.
Ограничения определяют область допустимых решений, а наклон прямой, отображающий целевую функцию, — точку последнего ее пересечения с областью допустимых решений, которая и является наилучшим решением задачи (оптимумом). В данном случае %%х_1 = 9%%, %%х_2 = 13%%.
В случае большего числа разнородных ограничений графическая интерпретация задачи затруднена, поэтому используются специальные методы (например, симплекс-метод), пакеты прикладных программ, их реализующие. В зависимости от вида целевой функции и принципов организации решения выделяют направления математического программирования: линейное (при линейном характере целевой функции), нелинейное (целевая функция нелинейна); целочисленное (ограничение на характер переменных), динамическое и т.п. эти направления имеют специфические особенности и методы решения. Но основная суть постановки задачи сохраняется.
Анализ хода постановки и решения задачи позволяет выявить следующие основные особенности математического программирования:
- введение понятий целевая функция, ограничения, ориентация на их формирование являются фактически некоторыми средствами постановки задачи; причем эти средства можно использовать, даже если не удается сформировать систему непротиворечивых ограничений или записать целевую функцию в формальном виде; поскольку в процессе проведения исследования можно уточнить представление о проблемной ситуации и, таким образом, поставить задачу хотя бы в первом приближении;
- при использовании методов математического программирования появляется возможность объединения в единой модели разнородных критериев (разных размерностей, предельных значений), что очень важно для отображения реальных проектных и производственных ситуаций;
- модель математического программирования допускает (и даже ориентирует на это) выход на границу области определения переменных (в то время, как методы классической математики требуют введения строгих начальных и граничных условий, значений которых переменная не может принимать в процессе анализа модели);
- изучение методов решения задач математического программирования позволяет получить представление о пошаговом приближении к решению, т.е. о пошаговом алгоритме получения результата моделирования;
- графическая интерпретация задачи дает наглядное представление об области допустимых решений (которая на рис. 2.4 заштрихована), что помогает в практических ситуациях даже в тех случаях, когда не удается получить формальное отображение целевой функции и строго решить задачу математического программирования.
Благодаря рассмотренным особенностям, методы математического программирования можно кратко охарактеризовать как методы, имеющие в отличие от классической математики некоторые средства постановки задачи. В частности, термин «целевая функция» часто используется даже в тех случаях, когда очевидна невозможность формального установления детерминированных взаимосвязей между компонентами и целями системы. Помогает в постановке задачи и понятие области допустимых решений. Этим объясняется популярность рассматриваемого направления; однако получаемые в таких случаях модели уже не относятся к моделям математического программирования и аналитическим методам.
Резюмируя, еще раз обратим внимание на то, что аналитические методы применяют в тех случаях, когда свойства системы можно отобразить с помощью детерминированных величин или зависимостей, т.е. когда знания о процессах и событиях в некотором интервале времени позволяют полностью определить их поведение вне этого интервала. Эти методы используются при решении задач движения и устойчивости, оптимального размещения, распределения работ и ресурсов, выбора наилучшего пути, оптимальной стратегии поведения, в том числе в конфликтных ситуациях и т.п.
В то же время при практическом применении аналитических представлений для отображения сложных систем следует иметь в виду, что они требуют установления всех детерминированных связей между учитываемыми компонентами и целями системы в виде аналитических зависимостей. Для сложных многокомпонентных, многокритериальных систем получить требуемые аналитические зависимости крайне трудно. Более того, даже если это и удается, то практически невозможно доказать правомерность применения таких выражений, т.е. адекватность модели рассматриваемой задаче. В таких ситуациях следует обратиться к другим методам моделирования.
5.7. Синтез систем управления методами математического программирования
Методы математического программирования относятся к численным методам поиска оптимальных решений, которые позволяют найти решение только для конкретных значений параметров. Содержание математического программирования составляют теория и методы решения задач о нахождении экстремумов функций на множествах, определяемых линейными и нелинейными ограничениями (равенствами и неравенствами). В упрощенной постановке задача оптимизации может быть сформулирована следующим образом.
Имеется набор параметров хх, хп и функция F(x). Требуется определить такую совокупность параметров из множества X, для которой функция ¥(х) принимает наибольшее или наименьшее значение. Функция F(x) получила название целевой функции.
Методы решения задач такого типа в литературе получили наименование методов математического программирования.
Термин «программирование» не связан с составлением программ для ЭВМ, но обусловлен тем, что при решении такого рода задач математическими средствами составляется программа действий.
Независимо от конкретной предметной ориентации задачи, решаемые методами математического программирования, с формальной точки зрения сводятся к одной постановке.
Yj a a x j > (=»-‘ <> »= 1 ‘ 2 ‘ т; ^ 0,у = 1, 2, п
необходимо найти совокупность параметров (план)
X = Х2, х„>, при котором функция (целевая функция)
F(x) = J jcjxj
принимает наибольшее или наименьшее значение.
ниями задачи. Дополнительно к условиям может быть задано требование целостности всех или нескольких переменных ху-.
Вектор X называется оптимальным планом задачи или оптимальным решением, так как его нахождение связано с отыскиванием конкретных значений параметров управления.
При решении задач математического программирования широко используются свойства линейных уравнений и неравенств, различные понятия, связанные с максимумами и минимумами функций, гладкими функциями, выпуклыми множествами и др.
Общая характеристика методов математического программирования
Методы математического программирования относятся к численным методам поиска оптимальных решений, которые позволяют найти решение только для конкретных значений параметров. Такими методами являются методы линейного, нелинейного дискретного, стохастического и динамического программирования.
Если функции эффективности и ограничения линейны, а операция одноэтапная, то можно применить один из методов линейного программирования. Данные методы используют одну и ту же идею: задается некоторое неоптимальное решение (начальный план), а затем оптимальное решение находится путем изменения начального плана в направлении приближения к оптимальному. Линейное программирование является в настоящее время наиболее разработанной ветвью математического программирования.
При нелинейном характере хотя бы одного компонента математической модели (целевой функции или ограничений) применяются методы нелинейного программирования. Общих методов этого типа пока не существует, за исключением случая квадратичной зависимости между критерием и параметрами при линейных ограничениях.
Некоторые математические модели могут содержать условие дискретности значений параметров (например, по своей физической сущности параметры должны быть только целыми числами). Решение таких задач осуществляется с применением методов дискретного (целочисленного) программирования.
Отыскание решений в операциях, которые носят многоэтапный характер, проводится с применением метода динамического программирования. Его сущность состоит в том, что оптимальное решение отыскивается не за все этапы одновременно, а последовательно от этапа к этапу. Идея оптимизации управления на каждом отдельном этапе использовалась давно, но без учета будущего. При динамическом программировании оптимизация каждого этапа проводится с учетом всех последующих этапов.
Если операция носит случайный характер и приходится иметь дело со случайными величинами и функциями, то для ее исследования используются методы стохастического программирования.