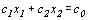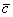Симплекс метод решения задач линейного программирования графическим методом

Линейное программирование. Решение задач

Ниже представлены примеры решения задач линейного программирования.

Линейное программирование. Решение задач графическим способом

Симплексный метод решения задач линейного программирования

1. Метод искусственного базиса
2. Задача оптимального производства продукции
3. Пример решения симлекс-методом
   Решить следующую задачу ЛП в неканонической форме симплекс-методом:
   f(x) = x₁ – x₂ – 3x₃ → min
4. М-метод. Решить задачу М-задачу.
5. Пример нахождения максимума функции симплексным методом
6. Пример нахождения минимума функции симплексным методом
7. Пример решения модифицированным симплекс-методом
8. Пример решения симплекс-методом в столбцовой форме записи
9. Симплекс-метод в строчечной форме записи. Пример решения
10. Пример решения задачи симплексным методом в Excel
11. Линейное программирование в Excel

Решение двойственной задачи линейного программирования

1. Двойственная задача ЛП
   Необходимо выполнить в указанном порядке следующие задания.
   1. Найти оптимальный план прямой задачи:
   а) графическим методом;
   б) симплекс-методом (для построения исходного опорного плана рекомендуется использовать метод искусственного базиса).
   2. Построить двойственную задачу.
   3. Найти оптимальный план двойственной задачи из графического решения прямой, используя условия дополняющей нежесткости.
2. Двойственная задача в Excel
3. Оценка целесообразности выпуска новой продукции

Двойственный симплекс-метод

Методы линейного программирования применяются для решения многих экстремальных задач, с которыми довольно часто приходится иметь дело в экономике. Решение таких задач сводится к нахождению крайних значений (максимума и минимума) некоторых функций переменных величин. Линейное программирование основано на решении системы линейных уравнений (с преобразованием в уравнения и неравенства), когда зависимость между изучаемыми явлениями строго функциональна. Для него характерны математическое выражение переменных величин, определенный порядок, последовательность расчетов (алгоритм), логический анализ. Применять его можно только в тех случаях, когда изучаемые переменные величины и факторы имеют математическую определенность и количественную ограниченность, когда в результате известной последовательности расчетов происходит взаимозаменяемость факторов, когда логика в расчетах, математическая логика, совмещаются с логически обоснованным пониманием сущности изучаемого явления. Методом линейного программирования решается транспортная задача, т.е. задача рационального прикрепления предприятий-потребителей к предприятиям-производителям.

Источник

§7.2 Графический метод и симплекс-метод решения задач линейного программирования Графический метод решения злп

Надо построить область допустимых решений системы ограничений. При этом возможны случаи:

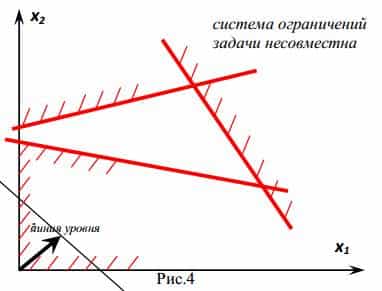
1) область допустимых решений — пустое множество;

2) область допустимых решений — единственная точка;

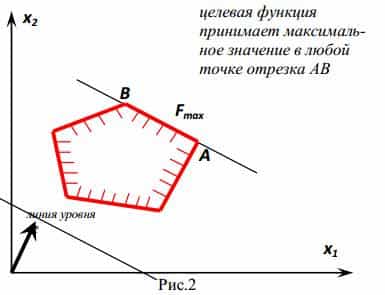
3) область допустимых решений — выпуклый многоугольник;

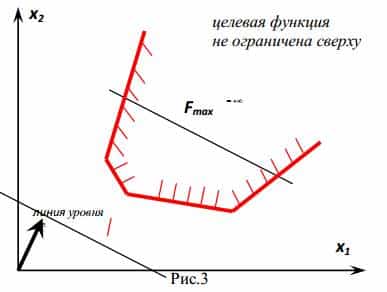
4) область допустимых решений — выпуклая неограниченная область.

В первом случае ЗЛП не имеет оптимального решения из-за несовместности системы ограничений.

Во втором случае — это единственное решение и будет оптимальным решением.

В третьем случае, чтобы найти оптимальное решение задачи, можно найти координаты всех угловых точек многоугольника, вычислить значения целевой функции во всех угловых точках. Наибольшее из этих значений и будет максимальным значением целевой функции, а наименьшее — минимальным, а координаты соответствующей угловой точки — оптимальным решением.

Существует другой способ, который позволяет графически сразу найти угловую точку, соответствующую оптимальному решению.

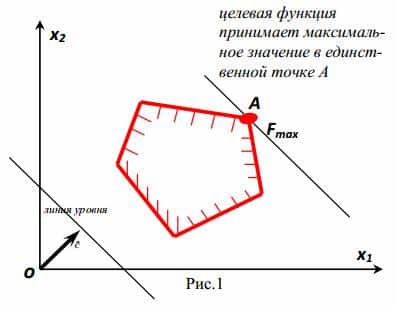
Пусть с₀ — некоторое число. Прямая является линией уровня целевой функции. В каждой точке этой прямой целевая функция принимает одно и то же значение, равное с₀. Вектор — градиент целевой функции

перпендикулярен к линиям уровня и показывает направление, в котором эта функция возрастает с наибольшей скоростью. Выбирая из линий уровня, проходящих через область допустимых решений, наиболее удаленную в направлениях вектора (в случае минимизации — в противоположном направлении), определим угловую точку, в которой целевая функция принимает максимальное (минимальное) значение.

Если экстремум достигается в двух угловых точках, то, по теореме об альтернативном оптимуме, оптимальным решением будет любая точка отрезка, соединяющего эти точки:

, .

В четвертом случае, когда область допустимых решений системы ограничений задачи неограниченная выпуклая область, оптимальное решение находится аналогично описанному выше. В данном случае оптимальное решение может совпадать с одной угловой точкой, с двумя угловыми точками и оптимальное решение может и не существовать из-за неограниченности целевой функции сверху в задаче на максимум или снизу в задаче на минимум.

Пример 1. Решить графически следующую задачу:

,

Построим область допустимых решений системы ограничений:

Источник

Графический метод решения ЗЛП

В линейном программировании используется графический метод, с помощью которого определяют выпуклые множества (многогранник решений). Если основная задача линейного программирования имеет оптимальный план, то целевая функция принимает значение в одной из вершин многогранника решений (см. рисунок).

Инструкция . Выберите количество строк (количество ограничений). Если количество переменных больше двух, необходимо систему привести к СЗЛП (см. пример и пример №2). Если ограничение двойное, например, 1 ≤ x₁ ≤ 4 , то оно разбивается на два: x₁ ≥ 1 , x₁ ≤ 4 (т.е. количество строк увеличивается на 1).
Построить область допустимого решения (ОДР) можно также с помощью этого сервиса.

Решение матричной игры
С помощью сервиса в онлайн режиме можно определить цену матричной игры (нижнюю и верхнюю границы), проверить наличие седловой точки, найти решение смешанной стратегии методами: минимакс, симплекс-метод, графический (геометрический) метод, методом Брауна.

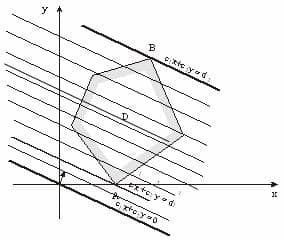
1. На плоскости X₁0X₂ строят прямые.
2. Определяются полуплоскости.
3. Определяют многоугольник решений;
4. Строят вектор N(c₁,c₂), который указывает направление целевой функции;
5. Передвигают прямую целевую функцию c₁x₂ + c₂x₂ = 0 в направлении вектора N до крайней точки многоугольника решений.
6. Вычисляют координаты точки и значение целевой функции в этой точке.

Целевая функция принимает экстремальное (минимальное или максимальное) значение в единственной точке А.

1. Сформулировать математическую модель задачи линейного программирования.
2. Решить задачу линейного программирования графическим способом (для двух переменных).

Если количество переменных в задаче линейного программирования больше двух, то задачу предварительно сводят к стандартной ЗЛП.
F(X) = 3x₁ — 2x₂ + 5x₃ — 4x₅ → max при ограничениях:
x₁ + x₂ + x₃=12
2x₁ — x₂ + x₄=8
— 2x₁ + 2x₂ + x₅=10
F(X) = 3x₁ — 2x₂ + 5x₃ — 4x₅
Переход к СЗЛП.
Расширенная матрица системы ограничений-равенств данной задачи:

1	1	1	0	0	12
2	-1	0	1	0	8
-2	2	0	0	1	10

Приведем систему к единичной матрице методом жордановских преобразований.
1. В качестве базовой переменной можно выбрать x₃.
2. В качестве базовой переменной можно выбрать x₄.
3. В качестве базовой переменной можно выбрать x₅.
Поскольку в системе имеется единичная матрица, то в качестве базисных переменных принимаем X = (3,4,5).
Соответствующие уравнения имеют вид:
x₁ + x₂ + x₃ = 12
2x₁ — x₂ + x₄ = 8
— 2x₁ + 2x₂ + x₅ = 10
Выразим базисные переменные через остальные:
x₃ = — x₁ — x₂+12
x₄ = — 2x₁ + x₂+8
x₅ = 2x₁ — 2x₂+10
Подставим их в целевую функцию:
F(X) = 3x₁ — 2x₂ + 5(- x₁ — x₂+12) — 4(2x₁ — 2x₂+10)
или
F(X) = — 10x₁ + x₂+20 → max
Система неравенств:
— x₁ — x₂+12 ≥ 0
— 2x₁ + x₂+8 ≥ 0
2x₁ — 2x₂+10 ≥ 0
Приводим систему неравенств к следующему виду:
x₁ + x₂ ≤ 12
2x₁ — x₂ ≤ 8
— 2x₁ + 2x₂ ≤ 10
F(X) = — 10x₁ + x₂+20 → max

Особенности решения задач линейного программирования графическим методом

Переменную x₂ принимаем в качестве дополнительной переменной и делаем замену на знак «≥»:
f=x₁ + 6x₃+ 27
x₁ + 3x₃≥6

Далее задача решается графическом способом.

Пример №2
F(X) = 3x₁ — 2x₂ + 5x₃ — 4x₅ → max при ограничениях:
x₁ + x₂ + x₃=12
2x₁ — x₂ + x₄=8
— 2x₁ + 2x₂ + x₅=10
F(X) = 3x₁ — 2x₂ + 5x₃ — 4x₅
Переход к СЗЛП.
Расширенная матрица системы ограничений-равенств данной задачи:

1	1	1	0	0	12
2	-1	0	1	0	8
-2	2	0	0	1	10

Приведем систему к единичной матрице методом жордановских преобразований.
1. В качестве базовой переменной можно выбрать x₃.
2. В качестве базовой переменной можно выбрать x₄.
3. В качестве базовой переменной можно выбрать x₅.
Поскольку в системе имеется единичная матрица, то в качестве базисных переменных принимаем X = (3,4,5).
Соответствующие уравнения имеют вид:
x₁ + x₂ + x₃ = 12
2x₁ — x₂ + x₄ = 8
— 2x₁ + 2x₂ + x₅ = 10
Выразим базисные переменные через остальные:
x₃ = — x₁ — x₂+12
x₄ = — 2x₁ + x₂+8
x₅ = 2x₁ — 2x₂+10
Подставим их в целевую функцию:
F(X) = 3x₁ — 2x₂ + 5(- x₁ — x₂+12) — 4(2x₁ — 2x₂+10)
или
F(X) = — 10x₁ + x₂+20 → max
Система неравенств:
— x₁ — x₂+12 ≥ 0
— 2x₁ + x₂+8 ≥ 0
2x₁ — 2x₂+10 ≥ 0
Приводим систему неравенств к следующему виду:
x₁ + x₂ ≤ 12
2x₁ — x₂ ≤ 8
— 2x₁ + 2x₂ ≤ 10
F(X) = — 10x₁ + x₂+20 → max

• Составить систему математических зависимостей (неравенств) и целевую функцию.
• Изобразить геометрическую интерпретацию задачи.
• Найти оптимальное решение.
• Провести аналитическую проверку.
• Определить существенные и несущественные ресурсы и их избытки.
• Определить значение целевой функции.
• Вычислить объективно обусловленные оценки.
• Составить соотношение устойчивости.

Источник