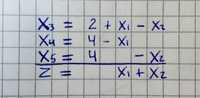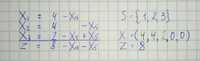Симплекс метод программа python

Current implementation does not use dual method.

The library provides one core function:

def linsolve( c, ineq_left=(), ineq_right=(), eq_left=(), eq_right=(), nonneg_variables = None, num=None, verbose=False, do_coerce=True):

• c : defines objective function. List of coefficients.
• ineq_left , ineq_right define set of inequality constraints.
• eq_left , eq_right define equality constraints
• nonneg_variables : list of variables (0-based integers) that are known to be non-negative.
• num Numeric system implementation (see "Generic computation" below). Defaults to finite-precision floating point numbers.

Consider the following problem: find maximum of the function 8x + 12y given the constraints:

This can be solved by the code:

A = [[2, 4 ], [0.5, 0.25], [2, 2.5 ]] C = [-8, -14] B = [440, 65, 320] resolution, sol = linsolve( C, ineq_left = A, ineq_right = B))

The resolution is RESOLUTION_SOLVED, and solution is [60, 80] .

An attempt is done to generalize calculations. This allows to solve LP problems, using arbitrary number implementations, not limiting to floating-point arithmetic. This is done by defining Typeclass objects, that are collections of methods for operations on numbers (naming inspired by Haskell).

Currently, 2 complete Typeclasses are provided:

• RealFiniteTolerance - uses float data type, default for numeric computations. This data type is imprecise by its nature, so tolerance value should be specified (default is 1e-6).
• RationalNumbers - performs exact, no rounding computations, using Python's built-in implementation of rational numbers: feactions.Fraction . Since computations are done exactly, no tolerance value is required.

Library user can define other type classes to work with different number implementations. Plausible extensions are sympy expressions, mpl numbers.

Each Typeclass is an object, providing a set of methods, defined in a base NumberTypeclass :

class NumberTypeclass: def zero(self): return 0 def one(self): return 1 def positive(self,x): return x > 0 def iszero(self,x): return x == 0 def nonnegative(self,x): return self.positive(x) or self.iszero(x) def coerce(self, x): return x def coerce_vec(self, x): return [self.coerce(xi) for xi in x] def coerce_mtx(self, x): return [self.coerce_vec(xi) for xi in x]

Redefine them to return and operate on values or required numeric type.

The coerce method is provided for testing convenience and not actually required by the algorithm. It converts value of arbitrary type to the numeric type, supported by the Typeclass.

The implementation is pure python, using lists internally. This could lead to inferior performance, when working with large-scale problems, using floating point numbers.

No serious attempt to optimize performance was done. Usage Tips

When possible, specify which variables of the problem are known to be non-negative. This improves performance and reduces memory use, because each variable or arbitrary sign is replaced by a difference of 2 non-negative variables.

Currently, purely redundant conditions of the form:

are not supported, algorithm incorrectly concludes that conditions are not satisfiable.

About

Pure Python implementation of Simplex Method for Linear Programming problem

Источник

Simplex Method With Python

Let’s start by trying the simplex method on a small example.

Maximize x₁ + x₂ subject to x₁ ≥ 0 x₂ ≥ 0 -x₁ + x₂ ≤ 2 x₁ ≤ 4 x₂ ≤ 4

As we know from the previous part we need to represent a linear program in an equational form for the simplex method.

Maximize x₁ + x₂ subject to -x₁ + x₂ + x₃ = 2 x₁ + x₄ = 4 x₂ + x₅ = 4 x₁, x₂, . x₅ ≥ 0

From an equational form, we express each linear program in the form of a simplex tableau.

The first three rows consist of the equations of the linear program, in which the slack variables have been carried over to the left-hand side and the remaining terms are on the right-hand side. The last row, separated by a line, contains a new variable z, which expresses the objective function.

Each simplex tableau is associated with a certain basic feasible solution. In our case we substitute 0 for the variables x₁ and x₂ from the right-hand side, and without calculation we see that x₃ = 2, x₄ = 4, x₅ = 4. This feasible solution is indeed basic with S= . The variables x₃, x₄, x₅ from the left-hand side are basic and the variables x₁, x₂ from the right-hand side are nonbasic. The value of the objective function z = 0 corresponding to this basic feasible solution can be read off from the last row of the tableau.

From the initial simplex tableau we will construct a sequence of tableaus of a similar form, by gradually rewriting them according to the certain rules. Each tableau will contain the same information about the linear program, only written differently. The procedure terminates with a tableau that represents the information so that the desired optimal solution can be read off directly.

Let us go to the next step. We try to increase the value of the objective function by increasing one of the nonbasic variables x₁ or x₂. Since we want to maintain feasibility, we have to be careful to let any of the basic variables go below zero. Let’s increase value of x₂ from 0 to 2. The most stringent restriction follows from the first equation, therefore we will express x₂ through it (x₂ = 2 + x₁ -x₃).

This process of rewriting one simplex tableau into another is called a pivot step. In each pivot step some nonbasic variable, in our case x₂, enters the basis, while some basic variable, in our case x₃, leaves the basis.

In the new tableau we can further increase the value of the objective function by increasing x₁, while increasing x₃, would lead to a smaller z-value. The maximum possible value for x₁ is 2. The most stringent restriction follows from the last equation (x₁ = 2 + x₃ -x₅).

In the same fashion, we will make the next step.

We reached the moment where nonbasic values can’t be increased without making the objective function value smaller. That means we found an optimal solution.

Programming

With a basic understanding of how the simplex algorithm works let’s write the first version of the algorithm.

We will pass to the algorithm linear program in equational representation that looks like this.

c = [1, 1, 0, 0, 0] A = [ [-1, 1, 1, 0, 0], [ 1, 0, 0, 1, 0], [ 0, 1, 0, 0, 1] ] b = [2, 4, 4]

The algorithm itself will consist of these steps:

1. Convert equational form to the tableau.
2. Until we reached the solution find pivot position and make pivot step.
3. Convert tableau to the solution of the linear program.

def simplex(c, A, b): tableau = to_tableau(c, A, b) while can_be_improved(tableau): pivot_position = get_pivot_position(tableau) tableau = pivot_step(tableau, pivot_position) return get_solution(tableau)

Tableau in the algorithm will contain all the information about the linear program, therefore, it will look different from what we had on paper. We will use this function to convert the equational form to the tableau.

 def to_tableau(c, A, b): xb = [eq + [x] for eq, x in zip(A, b)] z = c + [0] return xb + [z]

In the next function, we check where nonbasic values can be increased without making the objective function value smaller.

def can_be_improved(tableau): z = tableau[-1] return any(x > 0 for x in z[:-1])

If the value of an objective function can be improved we search for a pivot position.

import math def get_pivot_position(tableau): z = tableau[-1] column = next(i for i, x in enumerate(z[:-1]) if x > 0) restrictions = [] for eq in tableau[:-1]: el = eq[column] restrictions.append(math.inf if el  0 else eq[-1] / el) row = restrictions.index(min(restrictions)) return row, column

Next, we call function that will make pivot step and return new tableau.

def pivot_step(tableau, pivot_position): new_tableau = [[] for eq in tableau] i, j = pivot_position pivot_value = tableau[i][j] new_tableau[i] = np.array(tableau[i]) / pivot_value for eq_i, eq in enumerate(tableau): if eq_i != i: multiplier = np.array(new_tableau[i]) * tableau[eq_i][j] new_tableau[eq_i] = np.array(tableau[eq_i]) - multiplier return new_tableau

This function may seem a little bit confusing so let’s take a piece of paper and look at how tableau will change on each iteration.

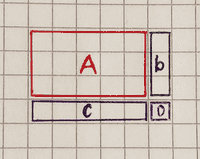
The final step in our algorithm is to extract the solution vector from the tableau. In the picture, we can see that columns where there is only one element equal to one and all other to zero have the same index as a basic variable in the right-hand tableau example.

def is_basic(column): return sum(column) == 1 and len([c for c in column if c == 0]) == len(column) - 1 def get_solution(tableau): columns = np.array(tableau).T solutions = [] for column in columns[:-1]: solution = 0 if is_basic(column): one_index = column.tolist().index(1) solution = columns[-1][one_index] solutions.append(solution) return solutions

Now, let’s run the algorithm.

Источник

Saved searches

Use saved searches to filter your results more quickly

You signed in with another tab or window. Reload to refresh your session. You signed out in another tab or window. Reload to refresh your session. You switched accounts on another tab or window. Reload to refresh your session.

Simplex method to solve linear programming models using Python 3 and Numpy

License

david-toro/SimplexMethod

This commit does not belong to any branch on this repository, and may belong to a fork outside of the repository.

Name already in use

A tag already exists with the provided branch name. Many Git commands accept both tag and branch names, so creating this branch may cause unexpected behavior. Are you sure you want to create this branch?

Sign In Required

Please sign in to use Codespaces.

Launching GitHub Desktop

If nothing happens, download GitHub Desktop and try again.

Launching GitHub Desktop

If nothing happens, download GitHub Desktop and try again.

Launching Xcode

If nothing happens, download Xcode and try again.

Launching Visual Studio Code

Your codespace will open once ready.

There was a problem preparing your codespace, please try again.

Latest commit

Git stats

Files

Failed to load latest commit information.

README.md

The simplex method is used in optimization to solve linear programming models, this is an implementation using, when needed, the Big M method to find the optimal value of the objective function and the vertex in which these value was found.

To execute the automated tests run the file test_simplex.py in the test package

Thanks to all the developers of Python, Numpy, Pycharm and Miniconda for making the building blocks that give life to this source code.

This project is licensed under the BSD 2-Clause License - see the LICENSE file for details

About

Simplex method to solve linear programming models using Python 3 and Numpy

Источник