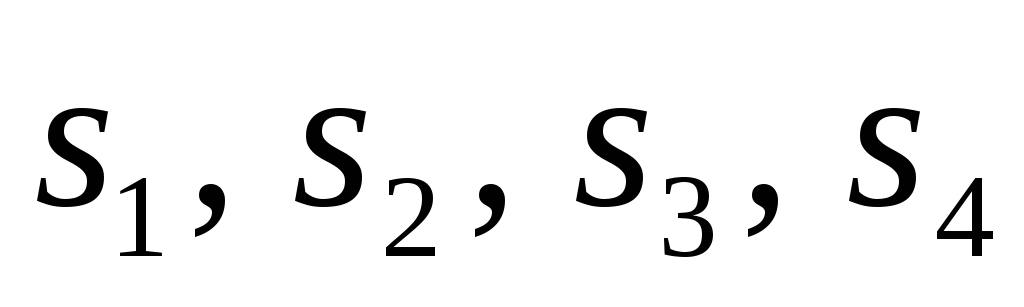1.3 Алгоритм симплекс-метода
Алгоритм симплекс-метода находит оптимальное решение, рассматривая ограниченное число допустимых базисных решений (опорных планов).
Алгоритм начинается всегда с некоторого допустимого опорного плана и затем пытается найти другой опорный базисный план, «улучшающий» значение целевой функции. Это возможно только в том случае, если возрастание какой-либо нулевой (небазисной) переменной ведет к улучшению значения целевой функции. Но для того, чтобы небазисная переменная стала положительной, надо одну из текущих базисных сделать нулевой (небазисной). Это необходимо, чтобы новое допустимое решение содержало в точности m базисных переменных. В соответствии с терминологией симплекс-метода выбранная нулевая переменная называется вводимой (в базис), а удаляемая базисная переменная – исключаемой (из базиса).
Алгоритм рассмотрим для наглядности на примере 1.1.
Приведем систему (1.1), (1.2) к каноническому виду:
Здесь — дополнительные переменные (остаточные), добавленные в неравенства для преобразования их в равенства.
Задачу ЛП в канонической форме для удобства будем представлять в виде таблицы 1.1.
Нижние четыре строки представляют равенства ограничений; значения правых частей этих равенств даны в столбце «Решение». Строка z получена из равенства z-5x1-4x2=0.
Дополнительные переменные 
составляют очевидное начальное допустимое базисное решение, которое отображается в столбце «Решение»: 
При этом
они не базисные. Значение целевой функции при этом базисном решении равно нулю.
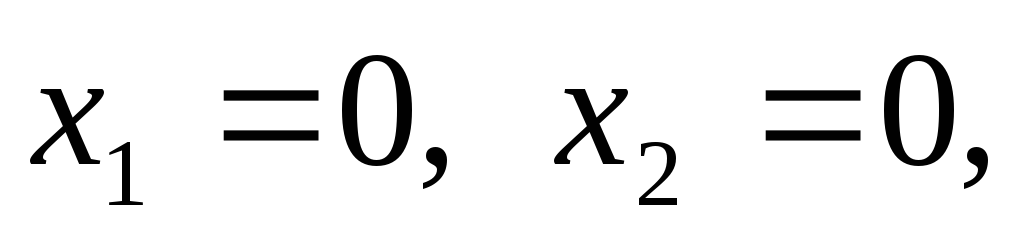
Будет ли начальное решение оптимальным? Конечно, нет, поскольку переменные х1 и х2 здесь равны нулю, а возрастание этих переменных даже на единицу приводит к увеличению значения целевой функции z=5x1+4x2 на 5 единиц или 4. Поскольку коэффициент при х1 больше, чем при х2, переменную х1 следует ввести в базис (в этом случае она станет вводимой). Если обратиться к таблице 1.1, то вводимая переменная определяется среди небазисных как переменная, имеющая наибольший отрицательный коэффициент в z-строке.
Включаемая переменная х1 должна принимать положительное значение. На рисунке 1.1 видно, что, исходя из начальной точки А (х1=0, х2=0), наибольшее значение, которое можно присвоить переменной х1 ( не выходя из множества допустимых решений), равно 4, что соответствует точке В (х1=4, х2=0). Это означает, что решение переместилось от крайней точки А в крайнюю точку В.
Алгебраически точку пересечения можно найти как отношение правой части равенства (значение в столбце «Решение») к коэффициенту при переменной х1 в этом равенстве, как показано в таблице 2.2.
При этом нас интересуют только неотрицательные отношения (или точка пересечения на положительной полуоси х1), так как они соответствуют направлению возрастания переменной х1. Отметим, что все значения в столбце «Решение» неотрицательны, поэтому вычисляемое отношение будет неотрицательным и конечным только в том случае, если знаменатель отношения строго положителен. Именно поэтому мы не рассматриваем отношения, соответствующие третьему и четвертому равенствам, так как там знаменатели или отрицательны, или равны нулю.
Минимальное неотрицательное отношение равно значению вводимой переменной х1 в новом решении, а именно х1=4. Значение целевой функции возрастает при х1=4 до 20 (=54).
Теперь среди текущих базисных переменных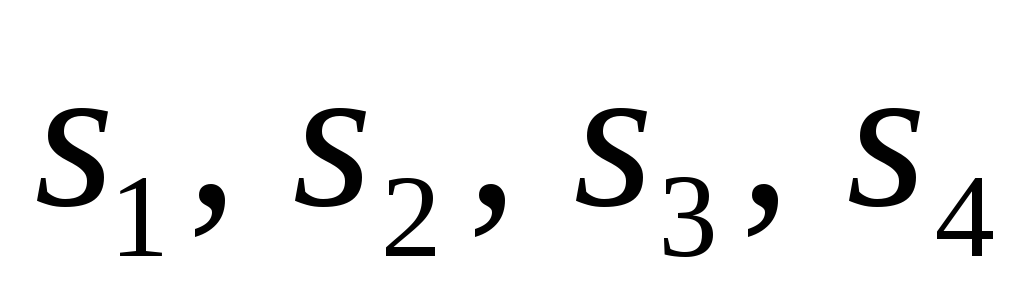 
следует определить исключаемую переменную, которая примет значение ноль после выведения ее из базиса и введения в базис переменной х1. (В нашем примере количество базисных переменных должно быть равно ровно 4). Поскольку наименьшее (неотрицательное) отношение соответствует переменной s1, то в точке В, именно эта переменная обращается в нуль. Таким образом, переменная s1 будет исключаемой, в этом случае переменная х1 автоматически получает значение, равное 4. Замена исключаемой переменной s1 на вводимую х1 приводит к новому базисному решению 
Вычисление нового базисного решения основывается на методе исключения переменных (методе Гаусса-Жордана). Для этого определим ведущий столбец, ассоциируемый с вводимой переменной, и ведущую строку, ассоциируемую с исключаемой переменной. Элемент, находящийся на пересечении ведущего столбца и ведущей строки называется ведущим элементом.
Для нашего примера ведущий столбец переменной х1 и ведущая строка s1 в таблице 1.1 выделены серой заливкой. Ведущим элементом будет число 6.
Процесс вычисления нового базисного решения состоит из двух этапов.
- Вычисление элементов новой ведущей строки. Новая ведущая строка = Текущая ведущая строка / Ведущий элемент.
- Вычисление элементов остальных строк, включая z-строку. Новая строка = Текущая строка — ее коэффициент в ведущем столбце* новая ведущая строка.
В нашем примере ведущая строка (s1 — строка) делится на ведущий элемент (=6). Вычисляем элементы остальных строк таблицы.
- z — строка.
текущаяz-строка: ( 1 -5 -4 0 0 0 0│ 0 ) -(-5)*Новая ведущая строка: ( 0 5 10/3 5/6 0 0 0│ 20 ) = Новая z- строка: ( 1 0 -2/3 5/6 0 0 0│ 20 ) - s2 — строка.
текущаяs2-строка: ( 0 1 2 0 1 0 0│ 6 ) —(1)*Новая ведущая строка: ( 0 -1 -2/3 -1/6 0 0 0│ -4 ) = Новаяs2— строка: ( 0 0 4/3 -1/6 1 0 0│ 2 ) - s3 — строка.
текущаяs3-строка: ( 0 -1 1 0 0 1 0│ 1 ) +(1)*Новая ведущая строка: ( 0 1 2/3 1/6 0 0 0│ 4 ) = Новаяs3— строка: ( 0 0 5/3 1/6 0 1 0│ 5 ) - s4 — строка. Новая s4 — строка повторяет текущую s4 — строку, поскольку ее коэффициент в ведущем столбце равен нулю.
Новая симплекс таблица, соответствующая новому базисному решению, имеет вид. Таблица 1.3
| Базис | z | x1 | x2 | s1 | s2 | s3 | s4 | Решение |
| z | 1 | 0 | -2/3 | 5/6 | 0 | 0 | 0 | 20 |
| х1 | 0 | 1 | 2/3 | 1/6 | 0 | 0 | 0 | 4 |
| s2 | 0 | 0 | 4/3 | -1/6 | 1 | 0 | 0 | 2 |
| s3 | 0 | 0 | 5/3 | 1/6 | 0 | 1 | 0 | 5 |
| s4 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 2 |
Отметим, что новая таблица 1.3 обладает теми же свойствами, что и начальная таблица 1.1: только небазисные переменные х2 и s1 равны нулю, в столбце «Решение» представлено новое базисное решение (
) вместе с новым значением целевой функцииz (=20). Это результат применения метода Гаусса-Жордана. Из последней таблицы видно, что полученное базисное решение не является оптимальным, поскольку в z-строке переменная х2 имеет отрицательный коэффициент. Увеличение значения х2 (ее текущее значение равно нулю) приведет к увеличению значения целевой функции. Таким образом, х2 должна быть введена в базис. Далее определим исключаемую переменную. Для этого вычислим отношения правых частей равенств, соответствующих ограничениям, к коэффициентам, стоящим при х2 в этих равенствах. Таблица 1.4
| Базис | x2 | Решение | Отношение |
| x1 | 2/3 | 4 | 4/(2/3)=6 |
| s2 | 4/3 | 2 | 2/(4/3)=3/2 минимум |
| s3 | 5/3 | 5 | 5/(5/3) = 3 |
| s4 | 1 | 2 | 2/1 = 2 |
В этой ситуации ведущей строкой будет s2 -строка, а ведущим столбцом- столбец, соответствующий переменной х2. Ведущий элемент равен 4/3. В таблице 1.3 они отмечены заливкой. Далее опять ведущую строку (s2 — строка) делим на ведущий элемент (4/3) и с помощью этой новой строки избавляемся от х2 во всех остальных строках, включая z — строку. В результате получится таблица 1.5. Таблица 1.5
| Базис | z | x1 | x2 | s1 | s2 | s3 | s4 | Решение |
| z | 1 | 0 | 0 | 3/4 | 1/2 | 0 | 0 | 21 |
| х1 | 0 | 1 | 0 | 1/4 | -1/2 | 0 | 0 | 3 |
| х2 | 0 | 0 | 1 | -1/8 | 3/4 | 0 | 0 | 3/2 |
| s3 | 0 | 0 | 0 | 3/8 | -5/4 | 1 | 0 | 5/2 |
| s4 | 0 | 0 | 0 | 1/8 | -3/4 | 0 | 1 | 1/2 |
Поскольку z-строка не имеет отрицательных коэффициентов, соответствующих небазисным переменным s1 и s2, полученное решение оптимально. Найденное оптимальное решение вместе с дополнительными переменными будет 
Значение целевой функцииz =21. C помощью последней симплекс-таблицы 1.5 можно получить много дополнительной информации, кроме решения:
- Состояние ресурсов.
- Цена единицы ресурсов.
- Все данные, необходимые для проведения анализа на чувствительность.
Это подробно будет описано в следующих Лекциях. Сформулируем два правила, а также рассмотрим последовательность действий, выполняемых при реализации симплекс-метода. Условие оптимальности Вводимой переменной в задаче максимизации (минимизации) является небазисная переменная, имеющая наибольший отрицательный (положительный) коэффициент в z-строке. Если в z-строке есть несколько таких коэффициентов, то выбор вводимой переменной берется произвольно. Оптимальное решение достигнуто тогда, когда в z-строке все коэффициенты при небазисных переменных будут неотрицательными (неположительными). Условие допустимости Как в задаче минимизации, так и в задаче максимизации в качестве исключаемой выбирается базисная переменная, для которой отношение правой части ограничения к положительному коэффициенту ведущего столбца минимально. Если базисных переменных с таким свойством несколько, то выбор исключаемой переменной выполняется произвольно. Последовательность действий, выполняемых в симплекс-методеШаг 0 Находится начальное допустимое решение. Шаг 1 На основе условия оптимальности определяется вводимая переменная. Если вводимых переменных нет, вычисления заканчиваются. Шаг 2 На основе условия допустимости выбирается исключаемая переменная. Шаг 3 Методом Гаусса-Жордана вычисляется новое базисное решение. Переход к шагу 1.
3.2. Симплекс-метод решения задач линейного программирования
Поскольку, как было показано в п. 3.1 решение задачи линейного программирования находится в одной из крайних (угловых) точек ОДЗ, важным вопросом является изучение не системы неравенств (4), а соответствующей системы уравнений AX = B, решение которой дает угловые точки ОДЗ.
Если уравнения системы АX = B линейно независимы, то система имеет множество решений при n > m и единственное решение при n = m. При решении задачи линейного программирования симплекс-методом всегда будет выполняться n > m, поэтому для получения некоторого одного решения, «лишние» n – m переменных приравниваются нулю.
Если приравнять к нулю n – m произвольных переменных (например, переменные xm+1, xm+2, …, xn) и, решив систему, найти значения оставшихся m переменных (x1, x2, …, xm), то такое решение называется базисным.
Если нулю приравнять некоторые другие n – m переменных – получим другое базисное решение. Любое базисное решение, у которого все переменные неотрицательные называется допустимым базисным решением.
Переменные, которые были приравнены нулю, называются небазисными. Оставшиеся т переменных, значение которых получены из решения системы, называются базисными.
Допустимое базисное решение представляет собой угловую вершину ОДЗ.
Решение задачи симплекс-методом сводится к направленному перебору смежных друг с другом угловых точек, которые представляют собой допустимые базисные решения.
Сформулируем в общем виде алгоритм симплекс-метода:
1: Приведение задачи к стандартной форме. Стандартной формой задачи линейного программирования будем называть задачу, у которой все ограничения записаны как равенства и при этом правые части ограничений неотрицательны.
2: Выделение исходного базисного решения (по возможности из стандартной формы). То есть определение тех переменных n – m переменных, которые приравниваются нулю и нахождение значений оставшихся базисных переменных.
3: Определение, является ли полученное базисное решение оптимальным, если да, то решение окончено, иначе переходим к шагу 4.
4: Определение переменной, которая войдет в базис и переменной, которая из базиса выйдет таким образом, чтобы новое решение было лучше предыдущего. То есть, если текущее базисное решение неоптимально, необходимо определить, какую из базисных переменных приравнять нулю, и какую из небазисных переменных вместо нее включить в базис.
5: Использование эквивалентных преобразований методом Жордана-Гаусса для нахождения нового допустимого базисного решения. Переход к шагу 3.
Чтобы привести задачу линейного программирования к стандартной форме необходимо:
1. Убедиться, что во всех ограничениях правые части bi неотрицательны. Если есть отрицательные правые части ограничений, такие ограничения нужно умножить на –1 (при этом учесть, что в ограничениях типа или знак ограничения изменится на противоположный).
2. К левой части ограничений типа нужно прибавить новую, дополняющую переменную S, которая уравнивала бы левую и правую часть и показывала бы насколько левая часть ограничения меньше правой.
в стандартном виде будет выглядеть так:
3. Из левой части ограничений типа нужно вычесть новую, избыточную переменную e, которая уравнивала бы левую и правую часть и показывала бы насколько левая часть ограничения больше правой.
в стандартном виде будет выглядеть так:
Дополняющие переменные S и избыточные e будем называть вспомогательными, в то время, как переменные x – основными.
Чтобы из стандартной формы сразу выделить базисное решение, необходимо в качестве базисных переменных выбрать те m переменных, каждая из которых встречается только в одном из уравнений и включена в него с коэффициентом, равным единице.
В качестве исходных базисных переменных в задачах с ограничениями удобно брать переменные S1, …, Sn.
Реализацию алгоритма симплекс-метода проиллюстрируем на следующем примере.
Пример 3.2. Мебельная фабрика может производить шкафы, столы, стулья. При изготовлении мебели используются древесина, труд рабочих на столярном и отделочном участках. Необходимое количество ресурсов для изготовления шкафов, столов и стульев приведено в таблице:
Таблица 3.1 – Исходные данные к примеру 3.2