Лекция № 14 Тема: Динамическое программирование.
Учебные цель: дать студентам представление о методах решения задач динамического программирования.
- Вентцель Е.С. Исследование операций: задачи, принципы, методология. – М.: Наука. Гл. ред. физ. мат. лит., 1988. – 208с.
- Лаговський В.В. Сторожук Є.А. Семко М.М. Математичне програмування у вправах і задачах. – К.: Ін-т математики НАН України, 2001ю – 96 с.
- Красс М.С., Чупрынов Б.П. Математические методы и модели для магистрантов экономики: Учебное пособие. — СПб: Питер, 2006. – 496 с.
- Монахов А.В. Математические методы анализа экономики. Учебное пособие. – СПб: Питер, 2002. – 176 с.
- Конюховский П. Математические методы исследования операций в экономике. СПб: Питер, 2002. –
1. Постановка задачи динамического программирования.
2. Основные идеи вычислительного метода динамического программирования. Принцип оптимальности Беллмана.
3. Экономические задачи, решаемые с помощью методов динамического программирования.
1. Постановка задачи динамического программирования.
Часто возникают ситуации, когда решение можно принять только в несколько приемов — шаг за шагом. В этом случае необходимо привлекать аппарат динамического программирования.
Отдельные задачи математического программирования обладают специфическими особенностями, которые позволяют свести их решение к рассмотрению некоторого множества более простых «подзадач». В результате вопрос о глобальной оптимизации некоторой функции сводится к поэтапной оптимизации промежуточных целевых функций. В динамическом программировании рассматриваются методы позволяющие путем поэтапной (многошаговой) оптимизации получить общий (результирующий) оптимум.
Обычно методами динамического программирования оптимизируют работу управляемых систем, эффект которых оценивается аддитивной или мультипликативной целевой функцией. Аддитивной называется такая функция нескольких переменных , значение которой вычисляется как сумма функций , зависящих только от одной переменной :
Слагаемые аддитивной целевой функции соответствуют эффекту решений, принимаемых на отдельных этапах управляемого процесса. По аналогии, мультипликативная функция распадается на произведение положительных функций различных переменных:
Поскольку логарифм функции типа (2) является аддитивной функцией, достаточно ограничиться рассмотрением функцией вида (1).
Изложим сущность вычислительного метода динамического программирования на примере задачи оптимизации:
> 0, > 0, j = 1, 2, … , n. (4)
2. Основные идеи вычислительного метода динамического программирования. Принцип оптимальности Беллмана.
Допустим, что применение классических методов оптимизации для решения задачи либо проблематично, либо просто невозможно.
Основной принцип подхода, реализуемого в динамическом программировании, заключён в замене решения исходной многомерной задачи последовательностью задач меньшей размерности.
Перечислим основные требования к задачам, выполнение которых позволяет применить данный подход:
1.Объектом исследования должна служить управляемая система (объект) с заданными допустимыми состояниями и допустимыми управлениями;
2. Задача должна позволять интерпретацию как многошаговый процесс, каждый шаг которого состоит из принятия решения о выборе одного из допустимых управлений, приводящих к изменению состояния системы;
3. Задача не должна зависеть от количества шагов и быть определенной на каждом из них;
4. Состояние системы на каждом шаге должно описывается одинаковым (по составу) набором параметром;
5. Последующее состояние, в котором оказывается система после выбора решения на k-том шаге, зависит только от данного решения и её состояния к началу k-того шага. Данное свойство является основным с точки зрения идеологии динамического программирования и называется отсутствием последствия.
Решение задач динамического программирования базируется на использовании принципа оптимальности, сформулированного математиком Р. Беллманом: если некоторая последовательность решении оптимальна, то отдельные последующие решения внутри ее оптимальны по отношению к предыдущим решениям или, другими словами, оптимальная стратегия решения многоэтапной задачи состоит из оптимальных решений для каждого отдельного этапа. В соответствии с этим принципом задачу решают, начиная с последнего этапа. Затем переходят к решению предыдущего этапа, отбрасывая возможные альтернативы, которые противоречат уже отработанному решению.
Применительно к дискретным условиям планирования/, которые возникают в экономических задачах, динамическое программирование – метод многошаговой оптимизации.
Алгоритм многошаговой оптимизации методом динамического программирования содержит следующие этапы.
1. Описывается процесс и выбираются параметры системы, образующие фазовое пространство или пространство состояний. Определяются управляющие воздействия на систему. Выбирается способ членения процесса на шаги. Вводятся обозначения переменных, позволяющие формализовать описание процесса.
2. Определяются функции эффекта (выигрыша) на i-том шаге в зависимости от состояния системы в начале этого шага и используются управления : .
3. Определяются функции, выражающие изменение состояния системы под влиянием управления на i-том шаге процесса: .
4. Составляется рекуррентное соотношение динамического программирования:
5. Определяется условно-оптимальный эффект (выигрыш) для последнего n-го шага рассматриваемого процесса: , а также соответствующее ему условно-оптимальное управление .
6. Определяются условные оптимальные выигрыши (эффекты) и соответствующие этим эффектам управления для предпоследнего, предпредпоследнего и т.д. до первого шагов процесса:
7. Определяется начальное состояние (если оно не задано), выбираются оптимальные эффекты и безусловные направления для первого, второго и т.д. до последнего n-го шага рассматриваемого процесса.
2. Постановка задачи динамического программирования
Общая постановка задачи динамического программирования формулируется следующим образом. Имеется некоторая управляемая система , характеризующаяся определенным набором параметров. В этой системе происходят какие-то процессы (экономические, производственные, технологические и т.п.), которые можно представить как многошаговые. На каждом шаге процессам в системе соответствуют определенные значения параметров, описывающихсостояние системы. Заданы условия, позволяющие определять или начальное, или конечное состояние системы, или оба этих состояния. Иногда задаются области начальных и конечных состояний. Поскольку управление системой осуществляется для достижения конкретной цели, то указан показатель эффективности управления, называемый целевой функцией, численно выражающий эффект («выигрыш»), получаемый при тот или ином управлении из множества допустимых управлений.
В экономических системах целевая функция может определять прибыль, затраты, рентабельность, объем производства и т.п.
Задача динамического программирования (ДП) состоит в выборе из множества допустимых управлений такого, которое переводит систему из начального состояния в конечное, обеспечивая при этом целевой функции экстремум (минимум или максимум в зависимости от ее экономической сути). Такое управление называется оптимальным.
П






Допустим, 



Рис. 1. График состояний системы.
П





Числовая характеристика этого результата называется функцией Беллмана и зависит от номера шага k и состояния системы S.
Задача динамического программирования формулируется следующим образом: требуется определить такое управление 

.
Особенности математической модели динамического программирования заключаются в следующем:
- задача оптимизации формулируется как конечный многошаговый процесс управления;
- целевая функция (выигрыш) является аддитивной и равна сумме целевых функций каждого шага:
- выбор управления
на каждом шаге зависит только от состояния системы k этому шагу
и не влияет на предшествующие шаги (нет обратной связи);
- состояние системы
после каждого шага управления зависит только от предшествующего состояния системы и этого управляющего воздействия
(отсутствие последействия) и может быть записало в виде уравнения состояния:
- на каждом шаге управление
зависит от конечного числа управляющих переменных, а состояние системы зависит — от конечного числа параметров;
- оптимальное управление представляет собой вектор
, определяемый последовательностью оптимальных пошаговых управлений:
, число которых и определяет количество шагов задачи.



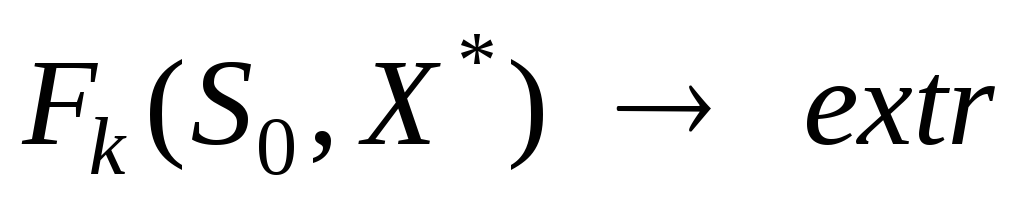

 на каждом шаге зависит только от состояния системы k этому шагу
на каждом шаге зависит только от состояния системы k этому шагу  и не влияет на предшествующие шаги (нет обратной связи);
и не влияет на предшествующие шаги (нет обратной связи);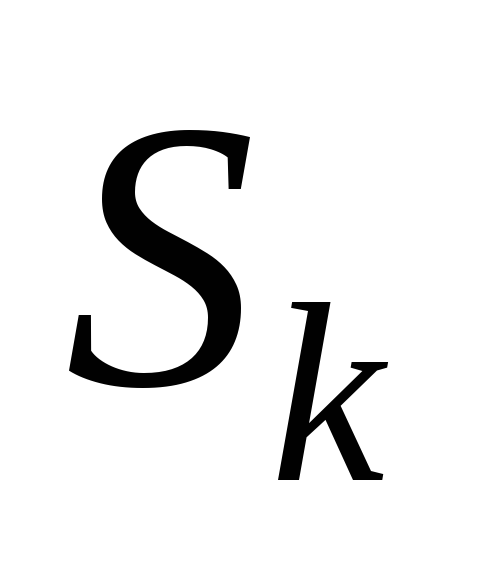 после каждого шага управления зависит только от предшествующего состояния системы и этого управляющего воздействия
после каждого шага управления зависит только от предшествующего состояния системы и этого управляющего воздействия 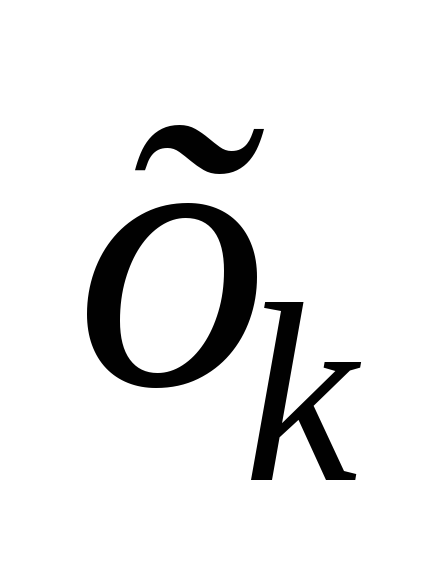 (отсутствие последействия) и может быть записало в виде уравнения состояния:
(отсутствие последействия) и может быть записало в виде уравнения состояния: 
 зависит от конечного числа управляющих переменных, а состояние системы зависит — от конечного числа параметров;
зависит от конечного числа управляющих переменных, а состояние системы зависит — от конечного числа параметров; , определяемый последовательностью оптимальных пошаговых управлений:
, определяемый последовательностью оптимальных пошаговых управлений: , число которых и определяет количество шагов задачи.
, число которых и определяет количество шагов задачи.