Selection Sort in Java
Sorting data is a frequent problem in computer science. Given a collection of elements, the goal is to rearrange them in some order. Common examples are sorting an array alphabetically or from smallest to largest.
Sorted data is a lot easier to manipulate. Finding the largest or smallest element of an array can be done in constant time if the array is sorted. Searching for an element is a lot faster using algorithms such as Binary Search which rely on the assumption that the array is already sorted.
One of the simplest algorithms for sorting data is Selection Sort. It’s usually taught in beginner programming classes and tutorials to explain the concept of sorting, so we’ll keep this article very beginner-friendly.
Selection Sort
Selection sort is an in-place comparison sorting algorithm that uses brute force to sort an array.
In-place means that the algorithm uses a small constant amount of space for extra storage.
It’s called a «brute force» algorithm because it uses the simplest and most ineffective way of calculating the solution. However, it does makes up for it with its straightforward implementation.
The algorithm divides the array into two subarrays:
The sorted subarray is empty in the beginning. In every iteration, the smallest element of the unsorted array will be appended to the end of the sorted array by swapping. This way, the sorted array will eventually contain all the elements of the original array.
An example array we want to sort in ascending order:
| Sorted array | Unsorted array | Minimal element of the unsorted array |
| [] | [16, 5, 30, 6, 2, 7] | 2 |
| [2] | [16, 5, 20, 6, 7] | 5 |
| [2, 5] | [16, 20, 6, 7] | 6 |
| [2, 5, 6] | [16, 7, 20] | 7 |
| [2, 5, 6, 7] | [16, 20] | 16 |
| [2, 5, 6, 7, 16] | [20] | 20 |
| [2, 5, 6, 7, 16, 20] | [] |
Implementation
The selectionSort() method takes just one argument, the array that needs to be sorted. We’ll iterate trough the unsorted array, which will be between indexes i and j , find it’s minimum and place it into the sorted array by swapping:
public static void selectionSort(int[] nums) < for (int i = 0; i < nums.length; i++) < // min is the index of the smallest element with an index greater or equal to i int min = i; for (int j = i + 1; j < nums.length; j++) < if (nums[j] < nums[min]) < min = j; >> // Swapping i-th and min-th elements int swap = nums[i]; nums[i] = nums[min]; nums[min] = swap; > > int[] array = new int[]16, 5, 30, 6, 7, 2>; selectionSort(array); System.out.println(Arrays.toString(array)); Selection Sort Time Complexity
Time complexity is a way to describe how much time an algorithm needs to finish executing relative to the size of the input. Analyzing the time it takes for an algorithm to give output is of crucial importance. Imagine a telephone book application that would take a day to sort all the numbers after a new number was added. That would be way less useful than the same app that would do it almost instantly.
Performance depends on the hardware as well as software, but the same program can be run on many different types of hardware. The Big-O notation makes it easier to approximate the time needed for a program to execute, regardless of software.
The average and worst-case time complexity of Selection Sort is O(n 2 ). This makes Selection Sort a lot slower than many other comparison sorting algorithms like Merge Sort or Insertion Sort which have the worst-case time complexity (O(nlogn)). Interestingly, O(nlogn) is the best that can be achieved by any comparison sorting algorithm.
Time Complexity Analysis
Showing that Selection Sort has quadratic time complexity comes down to calculating the number of times the inner loop will be iterated. We can see this if we go through the code line by line and try to approximate the time it takes to execute each line of code:
Everything in the inner block of the loop will be executed n times, where n is the length of a given array:
min will be initialized to i exactly n times. Now comes the tricky part:
Free eBook: Git Essentials
Check out our hands-on, practical guide to learning Git, with best-practices, industry-accepted standards, and included cheat sheet. Stop Googling Git commands and actually learn it!
Since this loop is nested, it takes a bit of math to calculate the number of times the block of code inside it will execute. Let’s work it out.
When i is equal to 0, j will go from 1 to n , meaning every instruction in the inner block will execute n times. When i increases to 1, j will stay between 2 and n , which implies the inner block will execute n-2 times. Summing this up:
The sum of a sequence of natural numbers is calculated using something called Gauss’s trick, and it results in (n 2 — n)/2. Simplifying this, results in O(n 2 ) time complexity.
Put simply, when calculating the complexity of an algorithm O(f(n)), we need to look for the highest power of n in the function f(n) and isolate it. This is because any part of the equation that has a lower power will not affect the result in any significant way.
For example, we have the function f(x) = x 2 +13x+23
O(f(x)) would be the highest power of x in the equation, which in this case is x 2 .
Here’s how it performed after sorting an array containing 10,000 integers in random order:
public static void main(String[] args) < int[] array = new int[10000]; for (int i = 0; i < array.length; i++) < array[i] = i; >// Shuffle array Collections.shuffle(Arrays.asList(array)); // Print shuffled collection System.out.println(Arrays.toString(array)); long startTime = System.nanoTime(); selectionSort(array); long endTime = System.nanoTime(); // Print sorted collection System.out.println(Arrays.toString(array)); // Print runtime in seconds System.out.println("Selection Sort runtime: " + (endTime - startTime)/1000000000); > Running it 10 times, this code produced the following results:
| Time(s) | Selection Sort |
| First Run | 0.024 |
| Second Run | 0.020 |
| Third Run | 0.022 |
| Fourth Run | 0.020 |
| Fifth Run | 0.025 |
| Sixth Run | 0.022 |
| Seventh Run | 0.021 |
| Eight Run | 0.031 |
| Ninth Run | 0.022 |
| Tenth Run | 0.029 |
The average run time was 0.0236 seconds, though, this will majorly depend on your machine as well.
Selection Sort Space Complexity
Space Complexity is also a big factor in algorithm design. Our programs are bound, not only by the time that they need to execute but also by memory usage. There is a limited amount of memory on any computer, so a programmer should keep an eye on that too.
The space complexity of Selection Sort is constant(O(1)) because it is in-place, which is great. Worst case complexity of Selection Sort is, unfortunately, O(n 2 ) as well, which means that even if the algorithm gets an already sorted array as input, it will still take a lot of time to return the unchanged array.
This algorithm has decent performance if the collection doesn’t have a lot of elements. If the array has ~10 elements, the difference in performance between different sorting algorithms shouldn’t be that noticeable, and Selection Sort might even outperform other divide-and-conquer algorithms.
Where Selection Sort shines, is when the number of swaps needs to be minimal. In the worst case, there will only be n-1 swaps, which is the minimal possible number of swaps that need to be performed. This is quite intuitive if consider that every element will be placed in its right spot in the sorted array right away.
Conclusion
Selection Sort is a brute force in-place comparison sort which continuously finds the minimum of an unsorted subarray and places it in the correct position in the sorted subarray. Due to its simplicity, it’s often one of the first algorithms that are taught in computer science courses all around the world.
Even if more efficient algorithms come built-it, it’s still important to understand the underlying logic and complexity analysis to avoid common issues and to make sure that the tool being used is the one that’s best suited for the job at hand.
Selection Sort – Data Structure and Algorithm Tutorials
Selection sort is a simple and efficient sorting algorithm that works by repeatedly selecting the smallest (or largest) element from the unsorted portion of the list and moving it to the sorted portion of the list.
The algorithm repeatedly selects the smallest (or largest) element from the unsorted portion of the list and swaps it with the first element of the unsorted part. This process is repeated for the remaining unsorted portion until the entire list is sorted.
How does Selection Sort Algorithm work?
Lets consider the following array as an example: arr[] =
First pass:
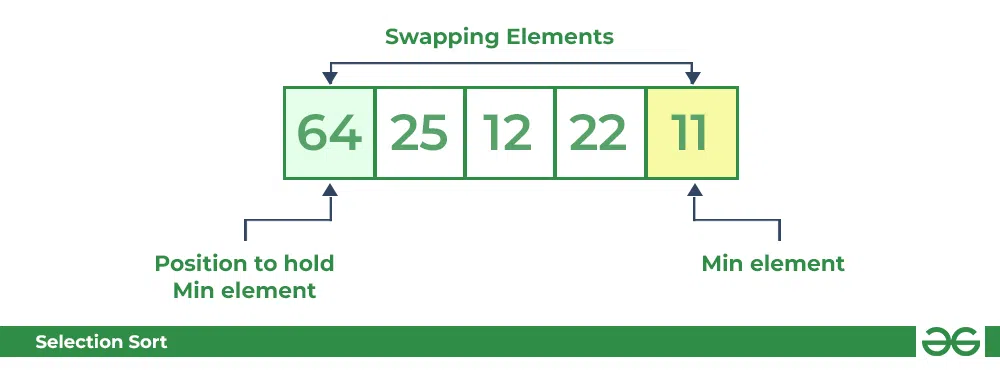
- For the first position in the sorted array, the whole array is traversed from index 0 to 4 sequentially. The first position where 64 is stored presently, after traversing whole array it is clear that 11 is the lowest value.
- Thus, replace 64 with 11. After one iteration 11, which happens to be the least value in the array, tends to appear in the first position of the sorted list.
Selection Sort Algorithm | Swapping 1st element with the minimum in array
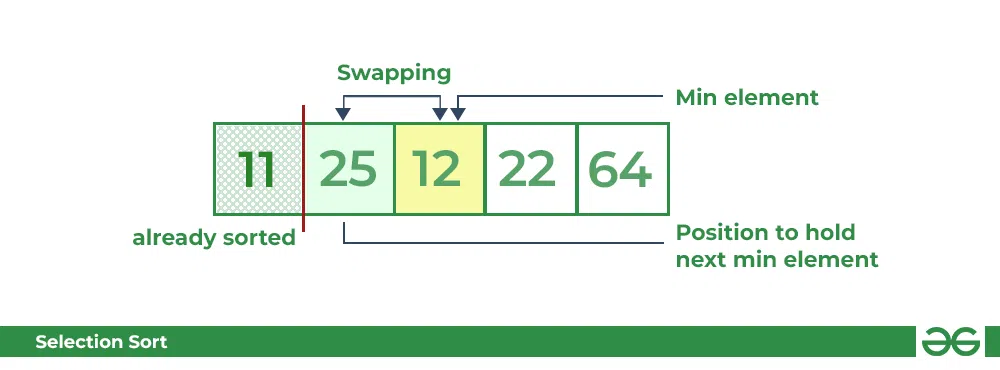
- For the second position, where 25 is present, again traverse the rest of the array in a sequential manner.
- After traversing, we found that 12 is the second lowest value in the array and it should appear at the second place in the array, thus swap these values.
Selection Sort Algorithm | swapping i=1 with the next minimum element
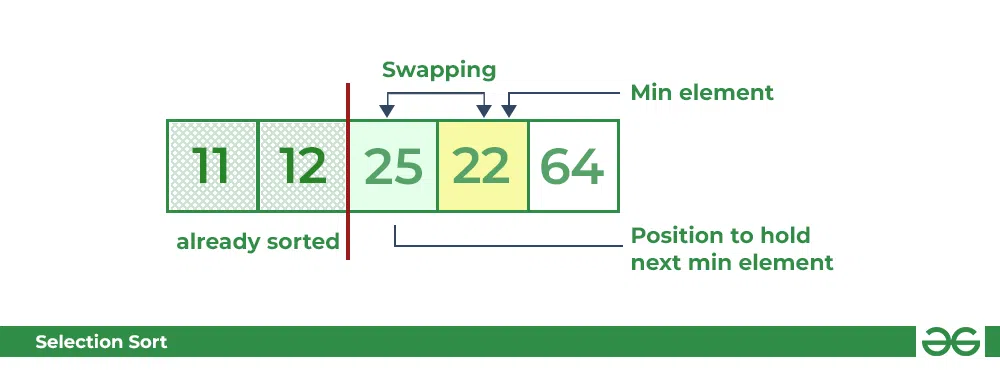
- Now, for third place, where 25 is present again traverse the rest of the array and find the third least value present in the array.
- While traversing, 22 came out to be the third least value and it should appear at the third place in the array, thus swap 22 with element present at third position.
Selection Sort Algorithm | swapping i=2 with the next minimum element
Fourth pass:
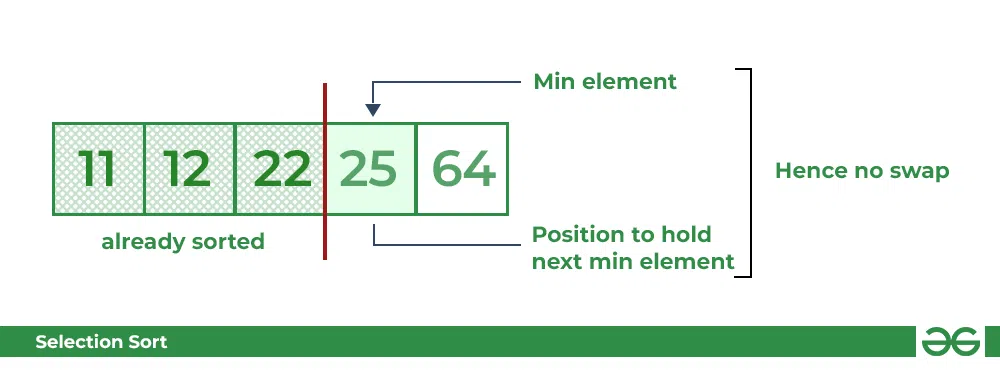
- Similarly, for fourth position traverse the rest of the array and find the fourth least element in the array
- As 25 is the 4th lowest value hence, it will place at the fourth position.
Selection Sort Algorithm | swapping i=3 with the next minimum element
- At last the largest value present in the array automatically get placed at the last position in the array
- The resulted array is the sorted array.
Selection Sort Algorithm | Required sorted array