Rounding number in python

How to Round Numbers in Python?

Rounding a number means making the number simpler by keeping its value intact but closer to the next number. Below are the following points that will cover in this article using Python:

• using Built-in round() Function
• using Truncation concept
• using Math.ceil() and Math.floor() functions
• using math.ceil
• using math.floor
• using Rounding Bias concept
• Rounding Half Away From Zero in Python

Input: 3.5 Output: 4 Explanation: Nearest whole number. Input: 3.74 Output: 3.7 Explanation: Rounded to one decimal place.

Round Numbers in Python using Built-in round() Function

In Python, there is a built-in round() function that rounds off a number to the given number of digits. The function round() accepts two numeric arguments, n, and n digits, and then returns the number n after rounding it to n digits. If the number of digits is not provided for rounding off, the function rounds off the given number n to the nearest integer.

python3

Round Numbers in Python using Truncation concept

In this function, each digit after a given position is replaced with 0. python truncate() function can be used with positive as well as negative numbers. The truncation function can be implemented in the following way:

• Multiplying the number by 10^p (10 raised to the p_th power) to shift the decimal point p places to the right.
• Taking the integer part of that new number using int().
• Shifting the decimal place p places back to the left by dividing by 10^p.

python3

Round Numbers in Python using Math.ceil() and Math.floor() functions

Math.ceil(): This function returns the nearest integer that is greater than or equal to a given number.
Math.floor(): This function returns the nearest integer less than or equal to a given number.

python3

Round Numbers in Python using math.ceil

In Rounding Up a number is rounded up to a specified number of digits. The rounding up function can be implemented in the following way:

• First, the decimal point in n is shifted to the correct number of places to the right by multiplying n by 10 ** decimals.
• The new value is rounded up to the nearest integer using math.ceil()
• Finally, the decimal point is shifted back to the left by dividing by 10 ** decimals.

python3

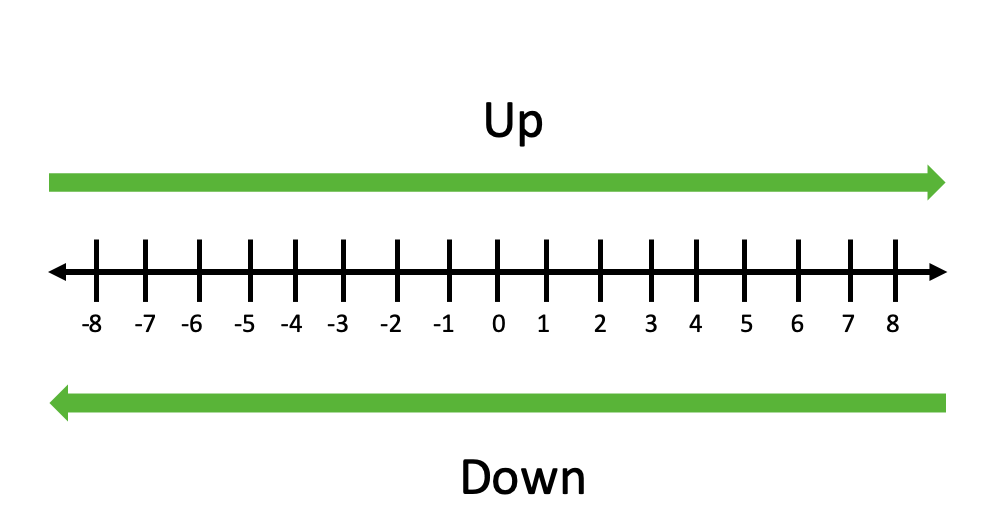
We can follow the diagram below to understand round up and round down. Round up to the right and down to the left.

Rounding up always rounds a number to the right on the number line and rounding down always rounds a number to the left on the number line.

Round Numbers in Python using math.floor

In Rounding Down a number is rounded down to a specified number of digits. The rounding down function can be implemented in the following way:

• First, the decimal point in n is shifted to the correct number of places to the right by multiplying n by 10 ** decimals.
• The new value is rounded up to the nearest integer using math.floor().
• Finally, the decimal point is shifted back to the left by dividing by 10 ** decimals.

python3

Round Numbers in Python using Rounding Bias concept.

The concept of symmetry introduces the notion of rounding bias, which describes how rounding affects numeric data in a dataset.
The rounding up strategy has a round towards positive infinity bias, as the value is always rounded up in the direction of positive infinity. Similarly, the rounding down strategy has a round towards negative infinity bias. The truncation strategy has a round towards negative infinity bias on positive values and a round towards positive infinity for negative values. Rounding functions with this behavior are said to have a round towards zero bias, in general.

a) Rounding Half Up concept in Python

The rounding half-up rounds every number to the nearest number with the specified precision and breaks ties by rounding up.
The rounding half-up strategy is implemented by shifting the decimal point to the right by the desired number of places. In this case, we will have to determine whether the digit after the shifted decimal point is less than or greater than equal to 5.
We can add 0.5 to the value which is shifted and then round it down with the math.floor() function.

Implementation of round_half_up() function:

Источник

№32 Функция round() / для начинающих

Round — встроенная функция Python. Ее задача — округлять число с плавающей точкой до той цифры, которую задает пользователь. Если ее не задать, то возвращается ближайшее целое число, ведь значением по умолчанию является 0. Функция round помогает «улучшать» числа с плавающей точкой.

Например, если округлить 4,5 до ближайшего целого, то вернется 5. Однако 4,7 будет результатом, если округлить до одной цифры 4,74. Быстрое округление — важный инструмент работы с такими числами.

• Число с плавающей точкой ( float_number ) представляет собой число, которое нужно округлить
• Количество дробей ( number_of_decimals ) определяет, до какой цифры будет округлено число. Функция возвращает float.
• Если количество цифр не указано, то по умолчанию там стоит ноль. В таком случае округление происходит до ближайшего целого и возвращается тоже целое число.

• Если >= 5, то добавляется +1.
• Если Примеры работы функции round в Python

Пример №1 — один параметр

 
# Целые числа 
a = 12 
round (a) 
print (a) 
 
# Десятичные числа 
b = 21.7 
c = 21.4 
print(round(b)) 
print(round(c)) 
 
Здесь возвращается целое число, до которого и округляется число с плавающей точкой.
 
Пример №2 — оба параметра
 
 
# когда последняя цифра 5 
a = 5.465 
print(round(a, 2)) 
 
# когда последняя цифра >=5 
b = 5.476 
print(round(b, 2)) 
 
# когда последняя цифра меньше 5 
c = 5.473 
print(round(c, 2)) 
 
Практические примеры
 
Пример №1 — функция round помогает при работе с дробями
 
Когда дроби нельзя конвертировать в десятичные дроби, в дело вступает функция round. После десятичной точки обычно много цифр, как например в случае с 22/7 (Pi). Но обычно используется не больше 2-4 цифр. Вспомогательный встроенный в round тип будет округлять до ближайшего кратного 10.
 
round(3.675, 2) вернет 3,67, а не 3,68. Удивительно, но это не баг. Результат указывает на то, что большая часть дробей не могут считаться точными числами с плавающей точкой.
 
 
a = 1/6 
print(a) 
print(round(a, 2)) 
 
Пример №2 — исключения и ошибки
 
Функция round округлит 2, 2,5 и 1,5 до 2. Это тоже не баг, а нормальное поведение функции.
 
 
a = 1.5 
b = 2 
c = 2.5 
print(round(a)) 
print(round(b)) 
print(round(c)) 
 
Если смотреть в целом, то работает функция вот так:
 
 
tup = (-40.95, 50.85, 10.98, 20.26, 30.05) # Создание кортежа 
lis = [-39.29, -42.15 , -39.97, -10.98, 32.65] # Создание списка 
print('Округление отрицательного десятичного числа = %.2f' %round(-19.48476)) 
print('Округление положительного десятичного числа = %.2f' %round(15.98763)) 
print('Округление со вторым параметром при положительном значении = %.3f' %round(11.98763, 3)) 
print('Округление со вторым параметром при отрицательном значении = %.3f' %round(-18.48476, 3)) 
print('Округление элементов в списке = %d' %round(lis[2])) 
print('Округление элементов в списке = %d' %round(lis[4])) 
print('Округление элементов в кортеже = %d' %round(tup[2])) 
print('Округление элементов в кортеже = %d' %round(tup[4])) 
print('Округление сумы чисел = %.2f' %round(20 + 40 - 20.6578, 2)) 
 
 
Округление отрицательного десятичного числа = -19.00 
Округление положительного десятичного числа = 16.00 
Округление со вторым параметром при положительном значении = 11.988 
Округление со вторым параметром при отрицательном значении = -18.485 
Округление элементов в списке = -40 
Округление элементов в списке = 33 
Округление элементов в кортеже = 11 
Округление элементов в кортеже = 30 
Округление сумы чисел = 39.34 
 
Есть разные метода функции округления в Python. Одна из них — это сокращение.
 
Сокращение
 
Сокращение используется для уменьшения размеров элементов. Это самый простой способ округления до конкретного числа. Для положительных чисел функция округляет их до ближайшего целого в меньшую сторону, а для отрицательных — в большую.
 
Например, round(565.5556, -2) используется как функция сокращения. Она вернет 600.
 
Выводы
 
Функция round позволяет упростить работу с крупными объемами данных. Ее задача — возвращать число с определенным количеством цифр после точки.
 
Источник