- How to rotate a matrix in JavaScript
- How to rotate a matrix in an array in javascript?
- Method 1: Using nested loops
- Method 2: Using transpose and reverse
- Method 3: Using swap and reverse
- How To Rotate A Matrix In JavaScript?
- Part 1 – The outer loop
- Part 2 – The inner loop
- Part 3 – Moving the elements
- Note
- Tips
- Complexity
- Summary
- Javascript Program to Inplace rotate square matrix by 90 degrees | Set 1
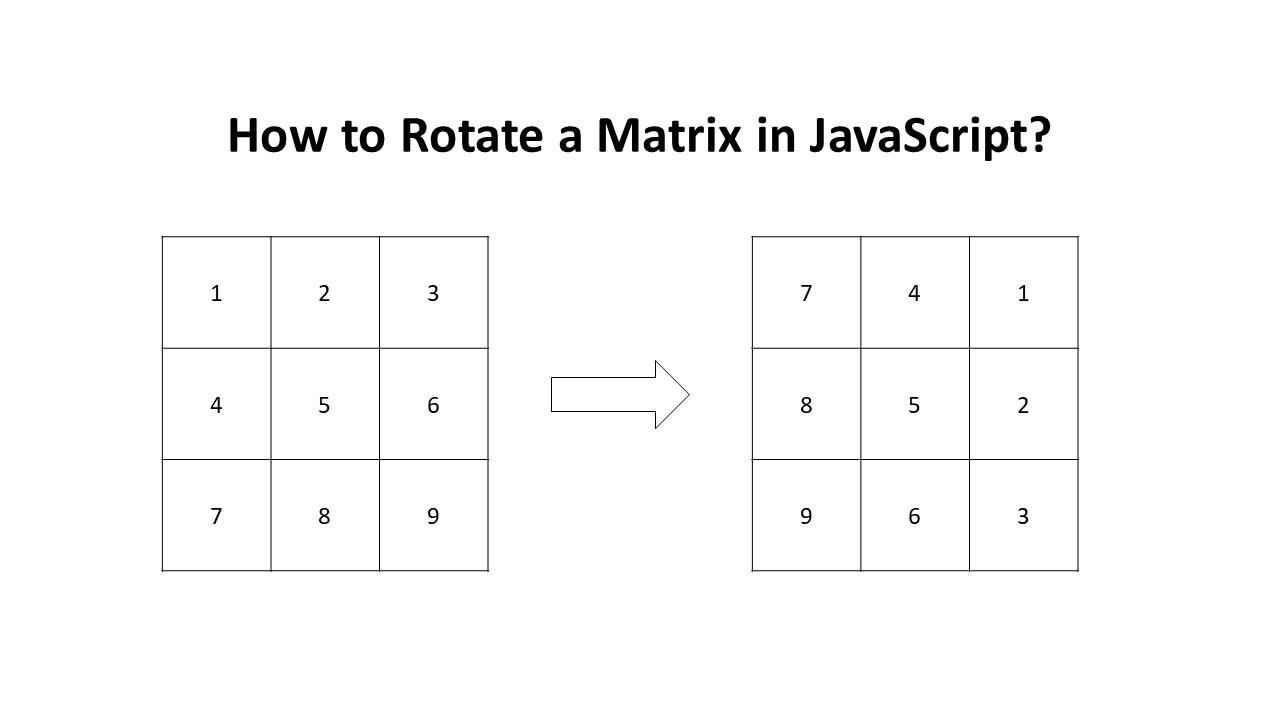
How to rotate a matrix in JavaScript
Here is one way of rotating a matrix in-place using JavaScript.
Space complexity: O(1).
Time complexity: O(n^2).
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576
function rotate(matrix, rotateCounterClockwise=false)rotateClockwise = !rotateCounterClockwise;if (matrix.length === 0 else if (rotateCounterClockwise) {const left = matrix[last-offset][first];// top -> leftmatrix[last-offset][first] = matrix[first][i]// right -> topmatrix[first][i] = matrix[i][last];// bottom -> rightmatrix[i][last] = matrix[last][last-offset];// left -> bottommatrix[last][last-offset] = left;}}}return matrix;}function geometricRotate(matrix, rotateCounterClockwise=false)if (matrix.length === 0 else if (rotateCounterClockwise) {reverseRows(matrix)transpose(matrix);}return matrix;}function transpose(matrix) {for (let i = 0; i < matrix.length; i++) {for (j = 0; j < i; j++) {[matrix[i][j], matrix[j][i]] = [matrix[j][i], matrix[i][j]]; // swap values}}}function reverseRows(matrix) {for (let i = 0; i < matrix.length; i++) {const row = matrix[i];row.reverse();}}rotate = geometricRotate;
Tests can be found at REPL.it
How to rotate a matrix in an array in javascript?
Rotating a matrix in an array can be a common requirement in JavaScript programming, especially when working with multi-dimensional arrays. This task can be accomplished in a number of ways, with different methods having varying levels of complexity and efficiency. Here, we will be discussing the various methods to rotate a matrix in an array in JavaScript.
Method 1: Using nested loops
To rotate a matrix in an array using nested loops in JavaScript, you can follow these steps:
- First, create an empty array to hold the rotated matrix.
- Then, iterate through the columns of the original matrix using a for loop.
- For each column, create a new row in the rotated matrix using another for loop.
- Within the inner for loop, iterate through the rows of the original matrix in reverse order.
- Append each element to the new row in the rotated matrix.
- Finally, return the rotated matrix.
function rotateMatrix(matrix) const rotatedMatrix = []; for (let col = 0; col matrix[0].length; col++) const newRow = []; for (let row = matrix.length - 1; row >= 0; row--) newRow.push(matrix[row][col]); > rotatedMatrix.push(newRow); > return rotatedMatrix; >This function takes a matrix as an argument and returns the rotated matrix. You can call this function like this:
const originalMatrix = [ [1, 2, 3], [4, 5, 6], [7, 8, 9] ]; const rotatedMatrix = rotateMatrix(originalMatrix); console.log(rotatedMatrix); // [[7, 4, 1], [8, 5, 2], [9, 6, 3]]In this example, the original matrix is a 3×3 matrix, and the rotated matrix is also a 3×3 matrix. The function uses nested loops to iterate through the columns and rows of the original matrix, and then appends the elements to the new rows in the rotated matrix.
Method 2: Using transpose and reverse
Sure, here’s how to rotate a matrix in an array in javascript using transpose and reverse:
function rotateMatrix(matrix) // Transpose the matrix for (let i = 0; i matrix.length; i++) for (let j = i; j matrix[0].length; j++) const temp = matrix[i][j]; matrix[i][j] = matrix[j][i]; matrix[j][i] = temp; > > // Reverse each row of the transposed matrix for (let i = 0; i matrix.length; i++) matrix[i].reverse(); > return matrix; >const matrix = [ [1, 2, 3], [4, 5, 6], [7, 8, 9] ]; const rotatedMatrix = rotateMatrix(matrix); console.log(rotatedMatrix);- First, we transpose the matrix by swapping each element with its corresponding element across the diagonal. This involves looping through the rows and columns of the matrix and swapping the elements at each corresponding position.
- Then, we reverse each row of the transposed matrix. This effectively rotates the matrix 90 degrees clockwise.
- Finally, we return the rotated matrix.
That’s it! This is a concise and efficient way to rotate a matrix in an array in javascript using transpose and reverse.
Method 3: Using swap and reverse
Sure, here’s an example of how to rotate a matrix in an array using swap and reverse method in JavaScript:
function rotateMatrix(matrix) // Step 1: Transpose the matrix for (let i = 0; i matrix.length; i++) for (let j = i; j matrix[0].length; j++) // Swap matrix[i][j] and matrix[j][i] let temp = matrix[i][j]; matrix[i][j] = matrix[j][i]; matrix[j][i] = temp; > > // Step 2: Reverse each row of the matrix for (let i = 0; i matrix.length; i++) matrix[i].reverse(); > return matrix; > // Example usage: let matrix = [ [1, 2, 3], [4, 5, 6], [7, 8, 9] ]; console.log(rotateMatrix(matrix)); // Output: [[7, 4, 1], [8, 5, 2], [9, 6, 3]]In the code above, we first transpose the matrix by swapping each element with its corresponding element in the opposite diagonal. We then reverse each row of the matrix to get the final rotated matrix.
The rotateMatrix function takes a matrix as an argument and returns the rotated matrix. We first loop through the matrix and swap matrix[i][j] with matrix[j][i] for each element above the diagonal. This effectively transposes the matrix.
We then loop through each row of the matrix and reverse it using the reverse method. This gives us the final rotated matrix.
How To Rotate A Matrix In JavaScript?
Rotating a matrix is one of the basic exercises for Data Structures and Algorithms, especially arrays. Matrix is a 2-Dimensional array after all. So, given a mxn 2-Dimensionanal matrix, how can you rotate a matrix in JavaScript? Here is the solution
// rotate the matrix by 90 degrees right function rotateMatrix(mtx) const len = mtx.length; for (let x = 0; x len/2; x++) for (let y = x; y len-x-1; y++) let temp = mtx[x][y]; // copy element from bottom left to top left mtx[x][y] = mtx[len-y-1][x]; // copy element from bottom right to bottom left mtx[len-y-1][x] = mtx[len-x-1][len-y-1]; // copy element from top right to bottom right mtx[len-x-1][len-y-1] = mtx[y][len-x-1]; // copy element from top left to top right mtx[y][len-x-1] = temp; > > >The solution’s simple but might be confusing at first. So, let me walk you through it.
(Note : to be specific, we are rotating a mxn 2-Dimensional array by 90 degrees to the right, algorithms might differ for different dimensions and different directions)
By the way, check this out if you need a definition for what a matrix is. (No, it’s not the movie with Keanu Reeves in it)
We can break the algorithm down to 3 main parts :
- Iterating to half the length of the outer array (the outer loop)
- Iterating the inner array
- Moving the elements
Before we dive into the steps, let me give you a study case to understand how the algorithm works better.
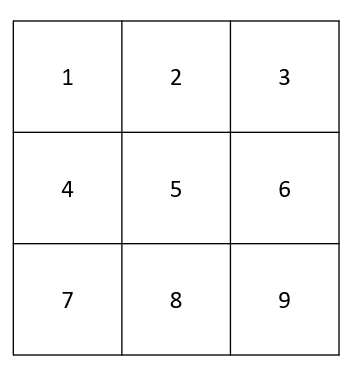
Here we have a 3×3 matrix example.
Part 1 – The outer loop
Since it is a nested array, we’d need nested loops to iterate through the elements. For the outer loop, we use for (let x = 0; x < len/2; x++) . It’s just a normal loop except that we are looping only until half the outer array length. So if we have a 3×3 matrix, the loop will run twice.
We only loop through to half of the outer array because we’re doing a rotation. We’re essentially switching elements from one side to the opposite side. If you’re swapping 4 items, you’ll only do it 2 times, right? So we do it to avoid re-rotating the elements.
So, following the study case, we’ll loop through [1, 2, 3] and [4, 5, 6]
Part 2 – The inner loop
The reasoning for the odd number of loops is the same as the outer loop, we want to avoid re-rotating the elements.
In the study case, we’ll be looping through :
- [1] and [2] for the first outer loop
- [ ] for the second outer loop. The outer loop requirement is achieved, but the conditions aren’t passed for the inner loops.
In the end, there are 2 activities done in the loops.
Part 3 – Moving the elements
In a loop, we’ll be moving 4 elements at a time. If you look at the matrix, you’ll notice there are actually only 8 elements that need to be rotated since the center is already in the correct position. So, we’ll be doing 2 loops.
We’re moving the loops by copying the elements to each other and also with a temporary variable. Look back to the code and you’ll see that we’re copying each element from a specific position to each other.
In the study case, the 2 loops done are as follows.
First, we rotate the corners, [1, 3, 9, 7]
And finally, our matrix is fully rotated.
Note
You’ll notice that there’s no return statement in the function. It’s because JavaScript is reference-based. So, it alters the original matrix directly.
Tips
To help you debug, I recommend logging the matrix at the step you’re confused about to see the matrix at that step.
But, as I tried logging, I’ve noticed that since JavaScript arrays are reference based, we’ll need a workaround to log the matrix which is shown below.
console.log(JSON.parse(JSON.stringify(mtx)));Complexity
We’re looping through most of the elements of the matrix. m is the row length and n is the column length.
We’re only using one array without creating a new array.
Summary
We basically loop the elements and switch between them. Hope that breakdown and visualization helps.
To understand it better, try visualizing a 4×4 matrix.
Since matrix is basically a nested array, it’ll be helpful to learn more about JavaScript Arrays With Big O Complexities!
For you who want to brush up your JavaScript skills, whether to deepen or learn form zero, I recommend you try Codecademy. There are tons of JavaScript lessons that you can learn in a structured and interactive way. You can learn from the most basic materials to advanced stuffs and even preparing for technical interviews. Go try it now!
If you have a better solution be it code-wise or efficiency-wise, please do comment below!
Check out the rest of my blog for more helpful contents on Data Structures and Algorithms in JavaScript!
Javascript Program to Inplace rotate square matrix by 90 degrees | Set 1
An approach that requires extra space is already discussed here.
Approach: To solve the question without any extra space, rotate the array in form of squares, dividing the matrix into squares or cycles. For example,
A 4 X 4 matrix will have 2 cycles. The first cycle is formed by its 1st row, last column, last row and 1st column. The second cycle is formed by 2nd row, second-last column, second-last row and 2nd column. The idea is for each square cycle, swap the elements involved with the corresponding cell in the matrix in anti-clockwise direction i.e. from top to left, left to bottom, bottom to right and from right to top one at a time using nothing but a temporary variable to achieve this.
Demonstration:
First Cycle (Involves Red Elements) 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 Moving first group of four elements (First elements of 1st row, last row, 1st column and last column) of first cycle in counter clockwise. 4 2 3 16 5 6 7 8 9 10 11 12 1 14 15 13 Moving next group of four elements of first cycle in counter clockwise 4 8 3 16 5 6 7 15 2 10 11 12 1 14 9 13 Moving final group of four elements of first cycle in counter clockwise 4 8 12 16 3 6 7 15 2 10 11 14 1 5 9 13 Second Cycle (Involves Blue Elements) 4 8 12 16 3 6 7 15 2 10 11 14 1 5 9 13 Fixing second cycle 4 8 12 16 3 7 11 15 2 6 10 14 1 5 9 13
- There is N/2 squares or cycles in a matrix of side N. Process a square one at a time. Run a loop to traverse the matrix a cycle at a time, i.e loop from 0 to N/2 – 1, loop counter is i
- Consider elements in group of 4 in current square, rotate the 4 elements at a time. So the number of such groups in a cycle is N – 2*i.
- So run a loop in each cycle from x to N – x – 1, loop counter is y
- The elements in the current group is (x, y), (y, N-1-x), (N-1-x, N-1-y), (N-1-y, x), now rotate the these 4 elements, i.e (x, y)
- Print the matrix.