Root mean square error in python

How to Calculate Root Mean Squared Error (RMSE) in Python

The root mean squared error (RMSE) is used to measured the differences between values predicted by the model and observed values of the model.

The root mean squared error (RMSE) is always non-negative, RMSE value near to 0 indicates a perfect fit to the data.

Root mean squared error or Root mean squared deviation (RMSD) is the square root of the average of squared errors. RMSD is measure of accuracy to compare forecasting errors of different models for a particular dataset.

In this tutorial, we will discuss about how to calculate root mean squared error (RMSE) in python.

RMSE Formula

The root mean squared error (RMSE) is defined as follows:

n = sample data points
y = predictive value for the j th observation
y^ = observed value for j th observation

For an unbiased estimator, RMSD is square root of variance also known as standard deviation. RMSE is the good measure for standard deviation of the typical observed values from our predicted model.

We will be using sklearn.metrics library available in python to calculate mean squared error, later we can simply use math library to square root of mean squared error value.

We will be using numpy library to generate actual and predication array.

pip install numpy

If you don’t have numpy package installed on your system, use below command in command prompt

pip install sklearn

If you don’t have sklearn package installed on your system, use below commands in command prompt

How to Calculate RMSE in Python

Lets understand with examples about how to calculate RMSE in python with given below python code

from sklearn.metrics import mean_squared_error from math import sqrt import numpy as np #define Actual and Predicted Array actual = np.array([10,11,12,12,14,18,20]) pred = np.array([9,10,13,14,17,16,18]) #Calculate RMSE result = sqrt(mean_squared_error(actual,pred)) # Print the result print("RMSE:", result)

In the above example, we have created actual and prediction array with the help of numpy package array function.

We then use mean_squared_error() function of sklearn.metrics library which take actual and prediction array as input value. It returns mean squared error value.

Later, we find RMSE value using square root of mean squared error value.

Above code returns root mean squared error (RMSE) value for given actual and prediction model is 1.85164

Lets check out root mean squared value (RMSE) calculation with few more examples.

Example 1 – RMSE Calculation

Lets assume, we have actual and predicted dataset as follows

Calculate RMSE for given model.

Here, again we will be using numpy package to create actual and prediction array and mean_squared_error() funciton of sklearn.metrics library for RMSE calculation in python.

Python code is given as below

from sklearn.metrics import mean_squared_error from math import sqrt import numpy as np #define Actual and Predicted Array actual = np.array([4,7,3,9,12,8,14,10,12,12]) pred = np.array([5,7,3,8,10,8,12,11,11,13]) #Calculate RMSE result = sqrt(mean_squared_error(actual,pred)) # Print the result print("RMSE:", result)

Above code returns root mean squared (RMSE) for given actual and prediction dataset is 1.14017

Example 2 – RMSE Calculation

Lets assume, we have actual and predicted dataset as follows

Calculate RMSE for given model.

Here, again we will be using numpy package to create actual and prediction array and mean_squared_error() funciton of sklearn.metrics library for RMSE calculation in python.

Python code is given as below

from sklearn.metrics import mean_squared_error from math import sqrt import numpy as np #define Actual and Predicted Array actual = np.array([14,17,13,19,12,18,14,10,12,12]) pred = np.array([15,14,14,18,10,16,12,11,11,13]) #Calculate RMSE result = sqrt(mean_squared_error(actual,pred)) # Print the result print("RMSE:", result)

Above code returns root mean squared (RMSE) for given actual and prediction dataset is 1.643167

Conclusion

I hope, you may find how to calculate root mean square (RMSE) in python tutorial with step by step illustration of examples educational and helpful.

RMSE is mostly used to find model fitness for given dataset. If RMSE has value 0, it means that its perfect fit as there is no difference in predicted and observed values.

Recent Posts

Источник

Как рассчитать RMSE в Python

Среднеквадратическая ошибка (RMSE) — это метрика, которая говорит нам, насколько далеко в среднем наши прогнозируемые значения от наших наблюдаемых значений в модели. Он рассчитывается как:

СКО = √[ Σ(P i – O i ) 2 / n ]

• Σ — причудливый символ, означающий «сумма».
• P i — прогнозируемое значение для i -го наблюдения
• O i — наблюдаемое значение для i -го наблюдения
• n — размер выборки

В этом руководстве объясняется простой метод расчета RMSE в Python.

Пример: расчет RMSE в Python

Предположим, у нас есть следующие массивы фактических и прогнозируемых значений:

actual= [34, 37, 44, 47, 48, 48, 46, 43, 32, 27, 26, 24] pred = [37, 40, 46, 44, 46, 50, 45, 44, 34, 30, 22, 23] 

Чтобы вычислить RMSE между фактическими и прогнозируемыми значениями, мы можем просто взять квадратный корень из функции mean_squared_error() из библиотеки sklearn.metrics:

#import necessary libraries from sklearn.metrics import mean_squared_error from math import sqrt #calculate RMSE sqrt(mean_squared_error(actual, pred)) 2.4324199198 

RMSE оказывается равным 2,4324 .

Как интерпретировать среднеквадратичную ошибку

RMSE — полезный способ увидеть, насколько хорошо модель соответствует набору данных. Чем больше RMSE, тем больше разница между прогнозируемыми и наблюдаемыми значениями, а это означает, что модель хуже соответствует данным. И наоборот, чем меньше RMSE, тем лучше модель соответствует данным.

Может быть особенно полезно сравнить RMSE двух разных моделей друг с другом, чтобы увидеть, какая модель лучше соответствует данным.

Источник

RMSE – Root Mean Square Error in Python

Hello readers. In this article, we will be focusing on Implementing RMSE – Root Mean Square Error as a metric in Python. So, let us get started!!

What is Root Mean Square Error (RMSE) in Python?

Before diving deep into the concept of RMSE, let us first understand the error metrics in Python.

Error metrics enable us to track the efficiency and accuracy through various metrics as shown below–

Mean Square error is one such error metric for judging the accuracy and error rate of any machine learning algorithm for a regression problem.

So, MSE is a risk function that helps us determine the average squared difference between the predicted and the actual value of a feature or variable.

RMSE is an acronym for Root Mean Square Error, which is the square root of value obtained from Mean Square Error function.

Using RMSE, we can easily plot a difference between the estimated and actual values of a parameter of the model.

By this, we can clearly judge the efficiency of the model.

Usually, a RMSE score of less than 180 is considered a good score for a moderately or well working algorithm. In case, the RMSE value exceeds 180, we need to perform feature selection and hyper parameter tuning on the parameters of the model.

Let us now focus on the implementation of the same in the upcoming section.

Root Mean Square Error with NumPy module

Let us have a look at the below formula–

So, as seen above, Root Mean Square Error is the square root of the average of the squared differences between the estimated and the actual value of the variable/feature.

In the below example, we have implemented the concept of RMSE using the functions of NumPy module as mentioned below–

• Calculate the difference between the estimated and the actual value using numpy.subtract() function.
• Further, calculate the square of the above results using numpy.square() function.
• Finally, calculate the mean of the squared value using numpy.mean() function. The output is the MSE score.
• At the end, calculate the square root of MSE using math.sqrt() function to get the RMSE value.

import math y_actual = [1,2,3,4,5] y_predicted = [1.6,2.5,2.9,3,4.1] MSE = np.square(np.subtract(y_actual,y_predicted)).mean() RMSE = math.sqrt(MSE) print("Root Mean Square Error:\n") print(RMSE)

Root Mean Square Error: 0.6971370023173351

RMSE with Python scikit learn library

In this example, we have calculated the MSE score using mean_square_error() function from sklearn.metrics library.

Further, have calculated the RMSE score through the square root of MSE as shown below:

from sklearn.metrics import mean_squared_error import math y_actual = [1,2,3,4,5] y_predicted = [1.6,2.5,2.9,3,4.1] MSE = mean_squared_error(y_actual, y_predicted) RMSE = math.sqrt(MSE) print("Root Mean Square Error:\n") print(RMSE)

Root Mean Square Error: 0.6971370023173351

Conclusion

By this, we have come to the end of this topic. Feel free to comment below, in case you come across any question.

For more such posts related to Python, Stay tuned and till then, Happy Learning!! 🙂

Источник

DataTechNotes

Original target data y and predicted label the yhat are the main sources to evaluate the model. We’ll start by loading the required modules for this tutorial.

import numpy as np import sklearn.metrics as metrics import matplotlib.pyplot as plt

Next, we’ll create sample y and yhat data to evaluate the model by the above metrics.

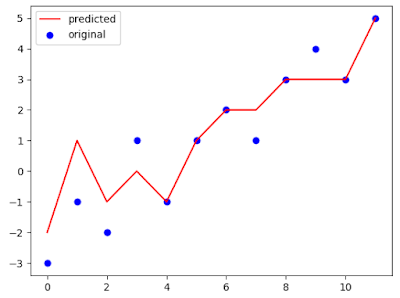
y = np.array([-3, -1, -2, 1, -1, 1, 2, 1, 3, 4, 3, 5]) yhat = np.array([-2, 1, -1, 0, -1, 1, 2, 2, 3, 3, 3, 5]) x = list(range(len(y)))

We can visualize them in a plot to check the difference visually.

plt.scatter(x, y, color="blue", label="original") plt.plot(x, yhat, color="red", label="predicted") plt.legend() plt.show()

Metrics calculation by formula

By using the above formulas, we can easily calculate them in Python.

# calculate manually d = y - yhat mse_f = np.mean(d**2) mae_f = np.mean(abs(d)) rmse_f = np.sqrt(mse_f) r2_f = 1-(sum(d**2)/sum((y-np.mean(y))**2)) print("Results by manual calculation:") print("MAE:",mae_f) print("MSE:", mse_f) print("RMSE:", rmse_f) print("R-Squared:", r2_f)

Results by manual calculation: MAE: 0.5833333333333334 MSE: 0.75 RMSE: 0.8660254037844386 R-Squared: 0.8655043586550436

Metrics calculation by sklearn.metrics

Sklearn provides the number of metrics to evaluate accuracy. The next method is to calculate metrics with sklearn functions.

mae = metrics.mean_absolute_error(y, yhat) mse = metrics.mean_squared_error(y, yhat) rmse = np.sqrt(mse) # or mse**(0.5) r2 = metrics.r2_score(y,yhat) print("Results of sklearn.metrics:") print("MAE:",mae) print("MSE:", mse) print("RMSE:", rmse) print("R-Squared:", r2)

Results of sklearn.metrics: MAE: 0.5833333333333334 MSE: 0.75 RMSE: 0.8660254037844386 R-Squared: 0.8655043586550436

The results are the same in both methods. You can use any method according to your convenience in your regression analysis.
In this post, we’ve briefly learned how to calculate MSE, MAE, RMSE, and R-Squared accuracy metrics in Python. The full source code is listed below.

import numpy as np import sklearn.metrics as metrics import matplotlib.pyplot as plt y = np.array([-3, -1, -2, 1, -1, 1, 2, 1, 3, 4, 3, 5]) yhat = np.array([-2, 1, -1, 0, -1, 1, 2, 2, 3, 3, 3, 5]) x = list(range(len(y))) plt.scatter(x, y, color="blue", label="original") plt.plot(x, yhat, color="red", label="predicted") plt.legend() plt.show() # calculate manually d = y - yhat mse_f = np.mean(d**2) mae_f = np.mean(abs(d)) rmse_f = np.sqrt(mse_f) r2_f = 1-(sum(d**2)/sum((y-np.mean(y))**2)) print("Results by manual calculation:") print("MAE:",mae_f) print("MSE:", mse_f) print("RMSE:", rmse_f) print("R-Squared:", r2_f) mae = metrics.mean_absolute_error(y, yhat) mse = metrics.mean_squared_error(y, yhat) rmse = np.sqrt(mse) #mse**(0.5) r2 = metrics.r2_score(y,yhat) print("Results of sklearn.metrics:") print("MAE:",mae) print("MSE:", mse) print("RMSE:", rmse) print("R-Squared:", r2)

Источник