Нелинейные системы и уравнения
Ищется решение нелинейного уравнения $$ \begin
В более общем случае мы имеем не одно уравнение (1), а систему нелинейных уравнений $$ \begin \tag f_i(x_1, x_2, \ldots, x_n) = 0, \quad i = 1, 2, \ldots n. \end $$ Обозначим через \( \mathbf = (x_1, x_2, \ldots, x_n) \) вектор неизвестных и определим вектор-функцию \( \mathbf(\mathbf) = (f_1(\mathbf), f_2(\mathbf), \ldots, f_n(\mathbf)) \). Тогда система (2) записывается в виде $$ \begin \tag \mathbf(\mathbf) = 0. \end $$ Частным случаем (3) является уравнение (1) (\( n = 1 \)). Второй пример (3) — система линейных алгебраических уравнений, когда \( \mathbf (\mathbf) = A \mathbf — \mathbf \).
Метод Ньютона
Решение нелинейных уравнений
При итерационном решении уравнений (1), (3) задается некоторое начальное приближение, достаточно близкое к искомому решению \( x^* \). В одношаговых итерационных методах новое приближение \( x_ \) определяется по предыдущему приближению \( x_k \). Говорят, что итерационный метод сходится с линейной скоростью, если \( x_ — x^* = O(x_k — x^*) \) и итерационный метод имеет квадратичную сходимость, если \( x_ — x^* = O(x_k — x^*)^2 \).
В итерационном методе Ньютона (методе касательных) для нового приближения имеем $$ \begin \tag x_ = x_k + \frac
Вычисления по (4) проводятся до тех пор, пока \( f(x_k) \) не станет близким к нулю. Более точно, до тех пор, пока \( |f_(x_k)| > \varepsilon \), где \( \varepsilon \) — малая величина.
Простейшая реализация метода Ньютона может выглядеть следующим образом:
def naive_Newton(f, dfdx, x, eps): while abs(f(x)) > eps: x = x - float(f(x))/dfdx(x) return x
Чтобы найти корень уравнения \( x^2 = 9 \) необходимо реализовать функции
def f(x): return x**2 - 9 def dfdx(x): return 2*x print naive_Newton(f, dfdx, 1000, 0.001)
Данная функция хорошо работает для приведенного примера. Однако, в общем случае могут возникать некоторые ошибки, которые нужно отлавливать. Например: пусть нужно решить уравнение \( \tanh(x) = 0 \), точное решение которого \( x = 0 \). Если \( |x_0| \leq 1.08 \), то метод сходится за шесть итераций.
-1.0589531343563485 0.9894042072982367 -0.784566773085775 0.3639981611100014 -0.03301469613719421 2.3995252668003453e-05 Число вызовов функций: 25 Решение: 3.0000000001273204
Теперь зададим \( x_0 \) близким к \( 1.09 \). Возникнет переполнение
-1.0933161820201083 1.104903543244409 -1.1461555078811896 1.3030326182332865 -2.064923002377556 13.473142800575976 -126055892892.66042
Возникнет деление на ноль, так как для \( x_7 = -126055892892.66042 \) значение \( \tanh(x_7) \) при машинном округлении равно \( 1.0 \) и поэтому \( f^\prime(x_7) = 1 — \tanh(x_7)^2 \) становится равной нулю в знаменателе.
Проблема заключается в том, что при таком начальном приближении метод Ньютона расходится.
Еще один недостаток функции naive_Newton заключается в том, что функция f(x) вызывается в два раза больше, чем необходимо.
- обрабатывать деление на ноль
- задавать максимальное число итераций в случае расходимости метода
- убрать лишний вызов функции f(x)
def Newton(f, dfdx, x, eps): f_value = f(x) iteration_counter = 0 while abs(f_value) > eps and iteration_counter 100: try: x = x - f_value/dfdx(x) except ZeroDivisionError as err: print("Ошибка: <>".format(err)) sys.exit(1) f_value = f(x) iteration_counter += 1 if abs(f_value) > eps: iteration_counter = -1 return x, iteration_counter
Метод Ньютона сходится быстро, если начальное приближение близко к решению. Выбор начального приближение влияет не только на скорость сходимости, но и на сходимость вообще. Т.е. при неправильном выборе начального приближения метод Ньютона может расходиться. Неплохой стратегией в случае, когда начальное приближение далеко от точного решения, может быть использование нескольких итераций по методу бисекций, а затем использовать метод Ньютона.
При реализации метода Ньютона нужно знать аналитическое выражение для производной \( f^\prime(x) \). Python содержит пакет SymPy, который можно использовать для создания функции dfdx . Для нашей задачи это можно реализовать следующим образом:
from sympy import symbol, tanh, diff, lambdify x = symbol.Symbol('x') # определяем математический символ x f_expr = tanh(x) # символьное выражение для f(x) dfdx_expr = diff(f_expr, x) # вычисляем символьно f'(x) # Преобразуем f_expr и dfdx_expr в обычные функции Python f = lambdify([x], # аргумент f f_expr) dfdx = lambdify([x], dfdx_expr) tol = 1e-1 sol, no_iterations = Newton(f, dfdx, x=1.09, eps=tol) if no_iterations > 0: print("Уравнение: tanh(x) = 0. Число итераций: <>".format(no_iterations)) print("Решение: <>, eps = <>".format(sol, tol)) else: print("Решение не найдено!") def F(x): y = np.zeros_like(x) y[0] = (3 + 2*x[0])*x[0] - 2*x[1] - 3 y[1:-1] = (3 + 2*x[1:-1])*x[1:-1] - x[:-2] - 2*x[2:] -2 y[-1] = (3 + 2*x[-1])*x[-1] - x[-2] - 4 return y def J(x): n = len(x) jac = np.zeros((n, n)) jac[0, 0] = 3 + 4*x[0] jac[0, 1] = -2 for i in range(n-1): jac[i, i-1] = -1 jac[i, i] = 3 + 4*x[i] jac[i, i+1] = -2 jac[-1, -2] = -1 jac[-1, -1] = 3 + 4*x[-1] return jac n = 10 guess = 3*np.ones(n) sol, its = Newton_system(F, J, guess) if its > 0: print("x = <>".format(sol)) else: print("Решение не найдено!")
Решение нелинейных систем
Идея метода Ньютона для приближенного решения системы (2) заключается в следующем: имея некоторое приближение \( \pmb^ \), мы находим следующее приближение \( \pmb^ \), аппроксимируя \( \pmb(\pmb^) \) линейным оператором и решая систему линейных алгебраических уравнений. Аппроксимируем нелинейную задачу \( \pmb(\pmb^) = 0 \) линейной $$ \begin \tag \pmb(\pmb^) + \pmb(\pmb^)(\pmb^ — \pmb^) = 0, \end $$ где \( \pmb(\pmb^) \) — матрица Якоби (якобиан): $$ \pmb(\pmb^) = \begin \frac<\partial f_1(\pmb^)> <\partial x_1>& \frac<\partial f_1(\pmb^)> <\partial x_2>& \ldots & \frac<\partial f_1(\pmb^)> <\partial x_n>\\ \frac<\partial f_2(\pmb^)> <\partial x_1>& \frac<\partial f_2(\pmb^)> <\partial x_2>& \ldots & \frac<\partial f_2(\pmb^)> <\partial x_n>\\ \vdots & \vdots & \ldots & \vdots \\ \frac<\partial f_n(\pmb^)> <\partial x_1>& \frac<\partial f_n(\pmb^)> <\partial x_2>& \ldots & \frac<\partial f_n(\pmb^)> <\partial x_n>\\ \end $$ Уравнение (5) является линейной системой с матрицей коэффициентов \( \pmb \) и вектором правой части \( -\pmb(\pmb^) \). Систему можно переписать в виде $$ \pmb(\pmb^)\pmb = — \pmb(\pmb^), $$ где \( \pmb = \pmb^ — \pmb^ \).
Таким образом, \( k \)-я итерация метода Ньютона состоит из двух стадий:
1. Решается система линейных уравнений (СЛАУ) \( \pmb(\pmb^)\pmb = -\pmb(\pmb^) \) относительно \( \pmb \).
2. Находится значение вектора на следующей итерации \( \pmb^ = \pmb^ + \pmb \).
Для решения СЛАУ можно использовать приближенные методы. Можно также использовать метод Гаусса. Пакет numpy содержит модуль linalg , основанный на известной библиотеке LAPACK, в которой реализованы методы линейной алгебры. Инструкция x = numpy.linalg.solve(A, b) решает систему \( Ax = b \) методом Гаусса, реализованным в библиотеке LAPACK.
Когда система нелинейных уравнений возникает при решении задач для нелинейных уравнений в частных производных, матрица Якоби часто бывает разреженной. В этом случае целесообразно использовать специальные методы для разреженных матриц или итерационные методы.
Можно также воспользоваться методами, реализованными для систем линейных уравнений.
Решение нелинейных уравнений#
Подмодуль scipy.optimize также содержит в себе методы для поиска корней нелинейных уравнений и их систем.
from matplotlib import pyplot as plt def configure_matplotlib(): plt.rc('text', usetex=True) plt.rcParams["axes.titlesize"] = 28 plt.rcParams["axes.labelsize"] = 24 plt.rcParams["legend.fontsize"] = 24 plt.rcParams["xtick.labelsize"] = plt.rcParams["ytick.labelsize"] = 18 plt.rcParams["text.latex.preamble"] = r""" \usepackage[utf8] \usepackage[english,russian] \usepackage """ configure_matplotlib()
Поиск корня скалярной функции одного аргумента#
Функция scipy.optimize.root_scalar позволяет искать корни функции \(f\colon \mathbb \to \mathbb\) :
Функция root_scalar предоставляет доступ к разным методам поиска корней, таким как newton , bisect , secant и многим другим. Какие-то из этих методов ищут корень внутри отрезка bracket , а другие ищут корень, начиная с какого-то начального приближения x0 .
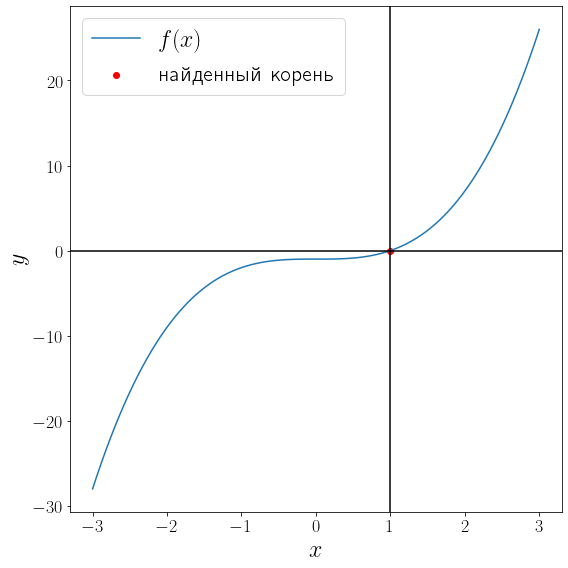
import numpy as np from scipy import optimize from matplotlib import pyplot as plt def f(x): return x**3 - 1 solution = optimize.root_scalar(f, bracket=[-10, 10], method="bisect") print(solution) x = np.linspace(-3, 3, 100) fig, ax = plt.subplots(figsize=(8, 8), layout="tight") ax.plot(x, f(x), label="$f(x)$") ax.scatter(solution.root, f(solution.root) , color="red", label="найденный корень") ax.axvline(solution.root, color="black") ax.axhline(0, color="black") ax.set_xlabel("$x$") ax.set_ylabel("$y$") ax.legend()
converged: True flag: 'converged' function_calls: 46 iterations: 44 root: 1.0000000000002274
Метод бисекции сошелся за 44 итерации. Проверим метод Ньютона.
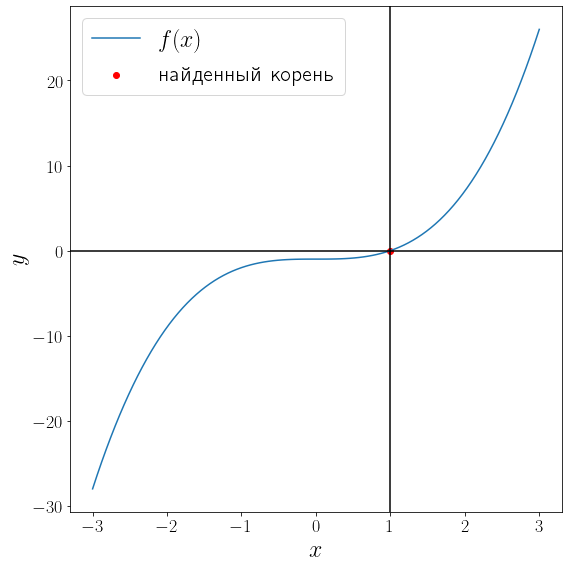
def fprime(x): return 3 * x**2 solution = optimize.root_scalar(f, fprime=fprime, x0=-2, method="newton") print(solution) fig, ax = plt.subplots(figsize=(8, 8), layout="tight") ax.plot(x, f(x), label="$f(x)$") ax.scatter(solution.root, f(solution.root) , color="red", label="найденный корень") ax.axvline(solution.root, color="black") ax.axhline(0, color="black") ax.set_xlabel("$x$") ax.set_ylabel("$y$") ax.legend()
converged: True flag: 'converged' function_calls: 20 iterations: 10 root: 1.0
Метод Ньютона сошелся за 11 итераций.
Решение системы нелинейных уравнений.#
Функция optimize.root предназначена для поиска корней уравнений вида
где \(x\in\mathbb^n\) и \(F\colon \mathbb^n \to \mathbb^n\) многомерны, т.е. optimize.root решает системы вида
Рассмотрим поиск корня на примере функции
Матрица Якоби этого уравнения имеет вид
\[\begin
а единственный действительный корень которой
В самом простом варианте достаточно передать методу optimize.root функцию левой части уравнения \(F\) и начальное приближение к корню.
import numpy as np from scipy import optimize from matplotlib import pyplot as plt def f(x): x = np.array(x) return np.array([ x[0] + 0.5 * (x[0] - x[1])**3 - 1.0, 0.5 * (x[1] - x[0])**3 + x[1] - 1.0 ]) solution = optimize.root(f, x0 = [0, 0]) print(solution)
fjac: array([[-1.00000000e+00, -1.09073861e-12], [ 1.09073861e-12, -1.00000000e+00]]) fun: array([0., 0.]) message: 'The solution converged.' nfev: 5 qtf: array([-2.18114415e-12, -2.18114415e-12]) r: array([-1.00000000e+00, -2.18119967e-12, -1.00000000e+00]) status: 1 success: True x: array([1., 1.])
Если известно аналитическое выражение для производно, то лучше задействовать его и передать по параметру jac .
def jac(x): return np.array([ [1 + 1.5 * (x[0] - x[1])**2, -1.5 * (x[0] - x[1])**2], [-1.5 * (x[1] - x[0])**2, 1 + 1.5 * (x[1] - x[0])**2] ]) solution = optimize.root(f, jac=jac, x0 = [0, 0], method="hybr") print(solution)
fjac: array([[-1., 0.], [ 0., -1.]]) fun: array([0., 0.]) message: 'The solution converged.' nfev: 2 njev: 1 qtf: array([1., 1.]) r: array([-1., -0., -1.]) status: 1 success: True x: array([1., 1.])