Решить графическим способом следующую двумерную задачу линейного программирования

Этапы решения графического метода задач линейного программирования

Пусть задача линейного программирования задана в двумерном пространстве, т. е. ограничения содержат две переменные, т.е. она может быть решена графически. Графический метод решения ЗЛП состоит из следующих этапов.

Сначала на координатной плоскости x₁Ox₂ строится допустимая многоугольная область (область допустимых решений, область определения), соответствующая ограничениям.

При этом могут быть получены следующие области:

1. Основной случай – получающаяся область имеет вид ограниченного выпуклого многоугольника (рис. 2.2, а).
2. Неосновной случай – получается неограниченный выпуклый многоугольник, имеющий вид, подобный изображенному на рис. 2.2, б.
3. Возможен случай, когда неравенства противоречат друг другу и допустимая область вообще пуста.

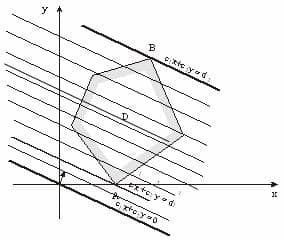
Рис. 2.2. Области определения решения:

а – основной случай, б – неосновной случай

Строится вектор , показывающий направление целевой функции. Этот вектор показывает направление наискорейшего изменения целевой функции. Прямая , перпендикулярная вектору–градиенту, является линией уровня целевой функции. В любой точке линии уровня целевая функция принимает одно и то же значение.

Приравняем целевую функцию постоянной величине “a”. Меняя значение “a”, получим семейство параллельных прямых, каждая из которых является линией уровня.

Важное свойство линии уровня линейной функции состоит в том, что при параллельном смещении линии в одну сторону уровень только возрастает, а при смещении в другую сторону – убывает.

При поиске максимума ЦФ необходимо передвигать целевую прямую в направлении вектора , при поиске минимума ЦФ – против направления вектора . Последняя по ходу движения вершина ОДР будет точкой максимума или минимума ЦФ.

Вычисляют координаты точки и значение целевой функции в этой точке. Для нахождения ее координат достаточно решить два уравнения прямых, получаемых из соответствующих ограничений и дающих в пересечении точку максимума.

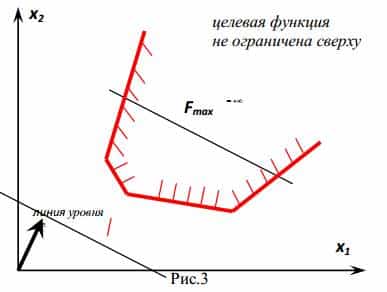
Если такой точки (точек) не существует, то можно сделать вывод о неограниченности ЦФ на множестве планов сверху (при поиске максимума) или снизу (при поиске минимум).

Пример. Решить задачу линейного программирования графическим способом.

Вернемся к целевой функции: . Допустим, значение функции L = 1 (абсолютно произвольно выбранное число), тогда . Данное уравнение является уравнением прямой на плоскости. Известно, что данная прямая перпендикулярна вектору, координатами которого являются коэффициенты функции, а именно вектору .

Следовательно, с геометрической точки зрения, исходная функция L изображается как множество прямых, перпендикулярных вектору .

Рис. 2.3. Допустимая область решения

Построим вектор , который изображен на рис. 2.3. Видно, что значение функции будет возрастать при перемещении прямой в направлении вектора . Будем перемещать прямую, перпендикулярную вектору , до тех пор, пока она полностью не пройдет область допустимых решений. В нашем случае касание прямой перед выходом из области допустимых решений произойдет в точке пересечении прямых и . В данной точке значение функции будет наибольшим.

Решая совместно эти два уравнения, получим координаты этой точки x₁ = 1; x₂ = 2. При этом значение целевой функции , что и дает ее максимальное значение.

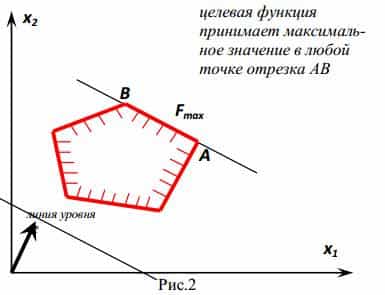
Следует обратить внимание на то, что оптимальный план, как правило, соответствует какой-то вершине многоугольника, изображающего допустимую область. Но может случиться так, что решение не будет единственным. Но и в этом случае вершины, соответствующие границам этой стороны, дают оптимальные планы нашей задачи линейного программирования. Таким образом, вершины допустимой области играют в решении задач линейного программирования особую роль. Если допустимая область не ограничена, то и значение целевой функции может быть неограниченным.

Подводя итог, можно сформулировать следующие положения:

1. Допустимая область – это выпуклый многоугольник.
2. Оптимум достигается в вершине допустимой области (если допустимая область ограничена и не пуста).
3. Ограниченность целевой функции в допустимой области является необходимым и достаточным условием разрешимости задачи.

Источник

Графический метод решения ЗЛП

В линейном программировании используется графический метод, с помощью которого определяют выпуклые множества (многогранник решений). Если основная задача линейного программирования имеет оптимальный план, то целевая функция принимает значение в одной из вершин многогранника решений (см. рисунок).

Инструкция . Выберите количество строк (количество ограничений). Если количество переменных больше двух, необходимо систему привести к СЗЛП (см. пример и пример №2). Если ограничение двойное, например, 1 ≤ x₁ ≤ 4 , то оно разбивается на два: x₁ ≥ 1 , x₁ ≤ 4 (т.е. количество строк увеличивается на 1).
Построить область допустимого решения (ОДР) можно также с помощью этого сервиса.

Решение матричной игры
С помощью сервиса в онлайн режиме можно определить цену матричной игры (нижнюю и верхнюю границы), проверить наличие седловой точки, найти решение смешанной стратегии методами: минимакс, симплекс-метод, графический (геометрический) метод, методом Брауна.

1. На плоскости X₁0X₂ строят прямые.
2. Определяются полуплоскости.
3. Определяют многоугольник решений;
4. Строят вектор N(c₁,c₂), который указывает направление целевой функции;
5. Передвигают прямую целевую функцию c₁x₂ + c₂x₂ = 0 в направлении вектора N до крайней точки многоугольника решений.
6. Вычисляют координаты точки и значение целевой функции в этой точке.

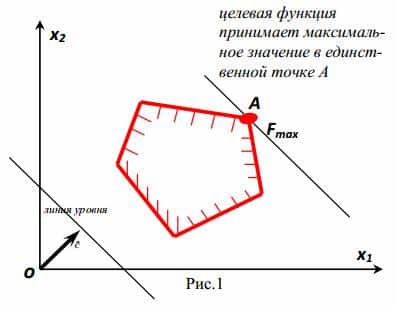
Целевая функция принимает экстремальное (минимальное или максимальное) значение в единственной точке А.

1. Сформулировать математическую модель задачи линейного программирования.
2. Решить задачу линейного программирования графическим способом (для двух переменных).

Если количество переменных в задаче линейного программирования больше двух, то задачу предварительно сводят к стандартной ЗЛП.
F(X) = 3x₁ — 2x₂ + 5x₃ — 4x₅ → max при ограничениях:
x₁ + x₂ + x₃=12
2x₁ — x₂ + x₄=8
— 2x₁ + 2x₂ + x₅=10
F(X) = 3x₁ — 2x₂ + 5x₃ — 4x₅
Переход к СЗЛП.
Расширенная матрица системы ограничений-равенств данной задачи:

1	1	1	0	0	12
2	-1	0	1	0	8
-2	2	0	0	1	10

Приведем систему к единичной матрице методом жордановских преобразований.
1. В качестве базовой переменной можно выбрать x₃.
2. В качестве базовой переменной можно выбрать x₄.
3. В качестве базовой переменной можно выбрать x₅.
Поскольку в системе имеется единичная матрица, то в качестве базисных переменных принимаем X = (3,4,5).
Соответствующие уравнения имеют вид:
x₁ + x₂ + x₃ = 12
2x₁ — x₂ + x₄ = 8
— 2x₁ + 2x₂ + x₅ = 10
Выразим базисные переменные через остальные:
x₃ = — x₁ — x₂+12
x₄ = — 2x₁ + x₂+8
x₅ = 2x₁ — 2x₂+10
Подставим их в целевую функцию:
F(X) = 3x₁ — 2x₂ + 5(- x₁ — x₂+12) — 4(2x₁ — 2x₂+10)
или
F(X) = — 10x₁ + x₂+20 → max
Система неравенств:
— x₁ — x₂+12 ≥ 0
— 2x₁ + x₂+8 ≥ 0
2x₁ — 2x₂+10 ≥ 0
Приводим систему неравенств к следующему виду:
x₁ + x₂ ≤ 12
2x₁ — x₂ ≤ 8
— 2x₁ + 2x₂ ≤ 10
F(X) = — 10x₁ + x₂+20 → max

Особенности решения задач линейного программирования графическим методом

Переменную x₂ принимаем в качестве дополнительной переменной и делаем замену на знак «≥»:
f=x₁ + 6x₃+ 27
x₁ + 3x₃≥6

Далее задача решается графическом способом.

Пример №2
F(X) = 3x₁ — 2x₂ + 5x₃ — 4x₅ → max при ограничениях:
x₁ + x₂ + x₃=12
2x₁ — x₂ + x₄=8
— 2x₁ + 2x₂ + x₅=10
F(X) = 3x₁ — 2x₂ + 5x₃ — 4x₅
Переход к СЗЛП.
Расширенная матрица системы ограничений-равенств данной задачи:

1	1	1	0	0	12
2	-1	0	1	0	8
-2	2	0	0	1	10

Приведем систему к единичной матрице методом жордановских преобразований.
1. В качестве базовой переменной можно выбрать x₃.
2. В качестве базовой переменной можно выбрать x₄.
3. В качестве базовой переменной можно выбрать x₅.
Поскольку в системе имеется единичная матрица, то в качестве базисных переменных принимаем X = (3,4,5).
Соответствующие уравнения имеют вид:
x₁ + x₂ + x₃ = 12
2x₁ — x₂ + x₄ = 8
— 2x₁ + 2x₂ + x₅ = 10
Выразим базисные переменные через остальные:
x₃ = — x₁ — x₂+12
x₄ = — 2x₁ + x₂+8
x₅ = 2x₁ — 2x₂+10
Подставим их в целевую функцию:
F(X) = 3x₁ — 2x₂ + 5(- x₁ — x₂+12) — 4(2x₁ — 2x₂+10)
или
F(X) = — 10x₁ + x₂+20 → max
Система неравенств:
— x₁ — x₂+12 ≥ 0
— 2x₁ + x₂+8 ≥ 0
2x₁ — 2x₂+10 ≥ 0
Приводим систему неравенств к следующему виду:
x₁ + x₂ ≤ 12
2x₁ — x₂ ≤ 8
— 2x₁ + 2x₂ ≤ 10
F(X) = — 10x₁ + x₂+20 → max

• Составить систему математических зависимостей (неравенств) и целевую функцию.
• Изобразить геометрическую интерпретацию задачи.
• Найти оптимальное решение.
• Провести аналитическую проверку.
• Определить существенные и несущественные ресурсы и их избытки.
• Определить значение целевой функции.
• Вычислить объективно обусловленные оценки.
• Составить соотношение устойчивости.

Источник

Решение задач линейного программирования
графическим методом

Существуют два наиболее распространенных способа решения задач линейного программирования (ЗЛП): графический метод и симплекс-метод. Графический метод существенно нагляднее и обычно проще для понимания и решения (хотя занимает много времени, так как требует тщательного построения чертежа). Также этот метод позволяет практически одновременно найти решение на минимум и максимум, тогда как симплекс-методом придется делать «два подхода».

Основные шаги по решению ЗПЛ графическим методом следующие: построить область допустимых решений задачи (выпуклый многоугольник), который определяется как пересечение полуплоскостей, соответствующих неравенствам задачи, построить линию уровня целевой функции, и, наконец, двигать линию уровня в нужном направлении, пока не достигнем крайней точки области — оптимальной точки (или множества). При этом можно найти единственное оптимальное решение (точку), множество (отрезок) или ни одного (область пустая или не ограниченная в нужном направлении).

А за конкретикой — к примерам ниже: вы найдете там решенные графическим способом задачи линейного программирования. Примеры решений выложены бесплатно для вашего удобства — изучайте, ищите похожие, решайте. Если вам нужна помощь в выполнении заданий по методам оптимальных решений, перейдите в раздел: Решение задач ЛП на заказ (решаем для студентов очников и заочников).

Графический метод решения ЗЛП: примеры онлайн

Задача 1. Колхоз имеет возможность приобрести не более 19 трехтонных автомашин и не более 17 пятитонных. Отпускная цена трехтонного грузовика — 4000 руб., пятитонного — 5000 руб. Колхоз может выделить для приобретения автомашин 141 тысяч рублей. Сколько нужно приобрести автомашин, чтобы их суммарная грузоподъемность была максимальной?
Задачу решить графическими и аналитическими методами.

Задача 2. Решить задачу графическим методом на минимум и на максимум

Задача 3. Решить задачу графическим методом на минимум и на максимум

Задача 4. Среди чисел x и y, удовлетворяющих условиям

найти такие, при которых разность этих чисел y-x принимает наибольшее значение.

Задача 5. Решить графическим методом ЗЛП, заданную указанной математической моделью.

Задача 6. Решите графически следующие задачи линейного программирования

Задача 7. Решить графическим методом

Источник

Пример 3. Решить графическим способом следующую двумерную задачу линейного программирования:

Решить графическим способом следующую двумерную задачу линейного программирования:

Рисунок 2.3.8.

Построение области допустимых решений целевой функции F.

Первое ограничение:

Второе ограничение:

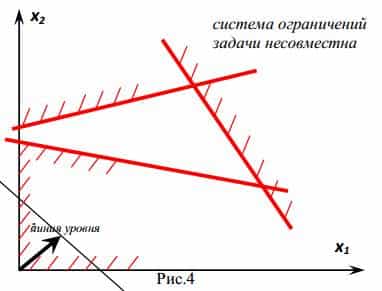
Ограничения задачи противоречивы, поэтому области допустимых решений не существует, следовательно, данная задача неразрешима.

Рисунок 2.3.9.

Рассмотрим случай, когда область допустимых решений существует. Здесь возможны два варианта:

1. Область допустимых решений ограниченна со всех сторон (примеры №1,2);

2. Область допустимых решений неограниченна с какой-либо стороны.

Примечание — Область допустимых решений всегда является выпуклым множеством. Множество S называется выпуклым, если для любых двух точек M и N этого множества весь отрезок MN содержится в множестве S. На рисунках изображены примеры выпуклых (рис. 1) и невыпуклых множеств (рис. 2).

Рисунок 2.3.10.

Рисунок 2.3.11.

Если область допустимых решений ограничена (она представляет собой замкнутый выпуклый N — угольник), то задача разрешима и экстремальное значение достигается в какой — либо вершине области допустимых решений. Исключение составляет тот случай, когда прямая уровня параллельна одной из сторон области допустимых решений, и по условию задачи ее надо перемещать именно в направлении этой стороны. Тогда оптимальное решение будет достигаться в любой точке, принадлежащей данной стороне.

Рассмотрим этот случай на примере.

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:

Источник