- Решение задачи линейного программирования вручную
- Графический способ решения задачи линейного программированя
- Решение задачи линейного программирования симплекс методом
- 6. Постановка задач линейного программирования. Примеры, различные формы задач и подходы решения. Постановка задач линейного программирования
- Примеры, различные формы задач и подходы решения
Решение задачи линейного программирования вручную
Графический способ решения задачи линейного программированя
- Переходим от системы неравенств содержащей ограничения, к системе уравнений.
- Строим соответствующие графики функций представленные прямой линией.
- Находим парные решения для уравнений.
;
,
Получаем что прямая
, заданная уравнением
, проходит через точки (3;0) и (2;3);
- Откладываем точки на координатной плоскости и строим график (прямую) проходящий через эти точки.
- Находим парные решения для уравнений.
- Определяем область решения. Берём произвольную точку на плоскости координат B(1; 1) и подставляем значения в первоначальное неравенство, если после решения неравенство верно, то полуплоскость которой принадлежит точка B, будет являться областью решения. Если неравенство ошибочно, то областью решения будет противоположная полуплоскость.
→Неравенство ошибочно.

- Аналогичным образом находим области решения для остальных уравнений.
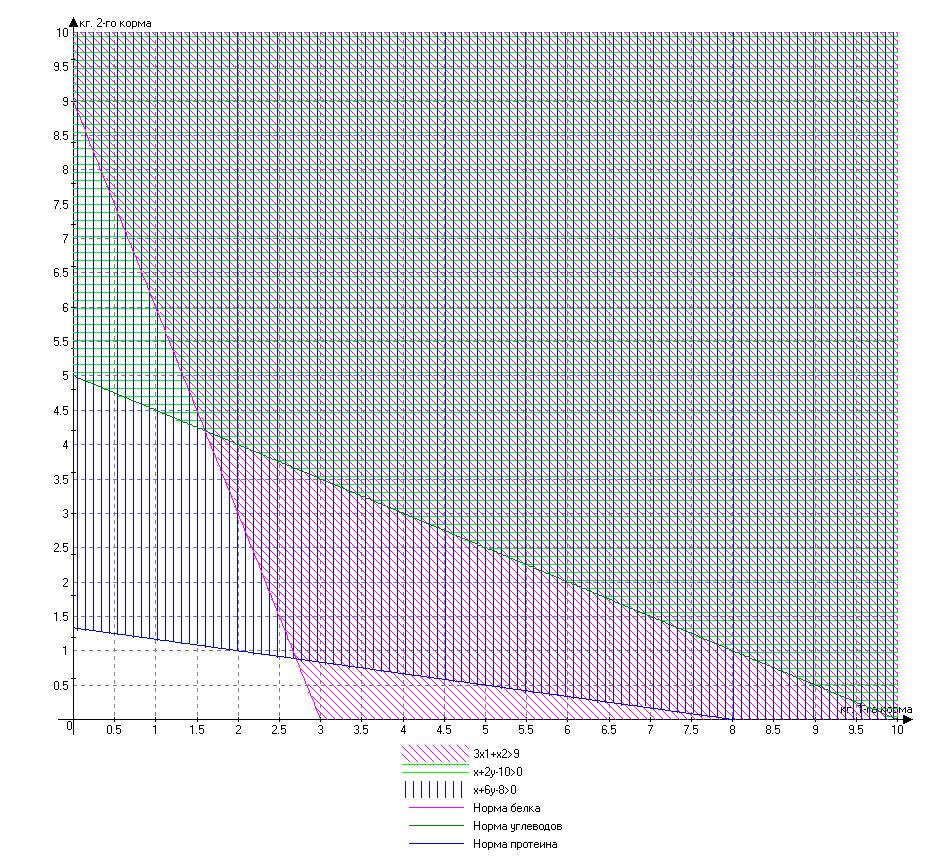
- Выделяем общую область допустимых решений, отвечающую всем ограничениям, поставленным в условиях задачи.

- Для нахождения экстремума целевой функции, от начала координат строим вектор градиент N(4; 6). Перпендикулярно ему строим вспомогательную линию Z, проходящую через вершины полученной области. Так как целевая функция задачи минимизация то, искомым оптимальным решением будет точка A, полученная пересечением области решения и вспомогательной линии, построенной первой по направлению вектора градиента.

- При решении системы уравнений используем метод подстановки. Для этого:
- Выразим
из первого уравнения
.
- Подставим во второе уравнение
.
- Находим
из полученного уравнения
Полученное значение подставляем в одно из исходных уравнений (первое) и находим
- Выразим
В результате решения системы получили
- Найдём значение целевой функции используя полученные значения Z(x) = 4·1.64+6·4.2 =31.6
Ответ. Наименьшие затраты 31.6 ден. ед. достигаются при составление рациона из 1.6 кг корма 1-го вида и 4.2 кг корма 2-го вида в сутки.
-
Решение задачи линейного программирования симплекс методом
- Приведем математическую модель задачи представленную в виде уравнений к каноническому виду.



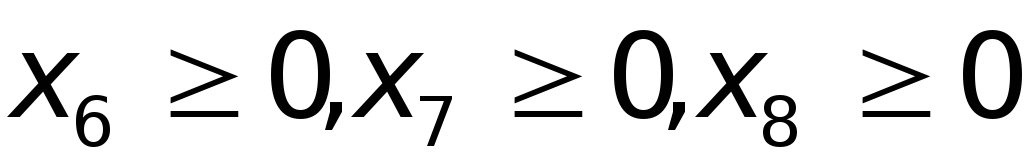
- Заполняем первую симплекс таблицу.
Таблица 3 Первая симлекс таблица
| Сб | Б | В | 4 | 6 | 0 | 0 | 0 | M | M | M | Q |
 |  |  |  |  |  |  |  | ||||
| M |  | 9 | 3 | 1 | -1 | 0 | 0 | 1 | 0 | 0 | |
| M |  | 10 | 1 | 2 | 0 | -1 | 0 | 0 | 1 | 0 | |
| M |  | 8 | 1 | 6 | 0 | 0 | -1 | 0 | 0 | 1 | |
| L | Z | ||||||||||
| ∆ | |||||||||||
При расчёте опорного плана используем M=1000. 
- Рассчитываем опорный план таблицы.
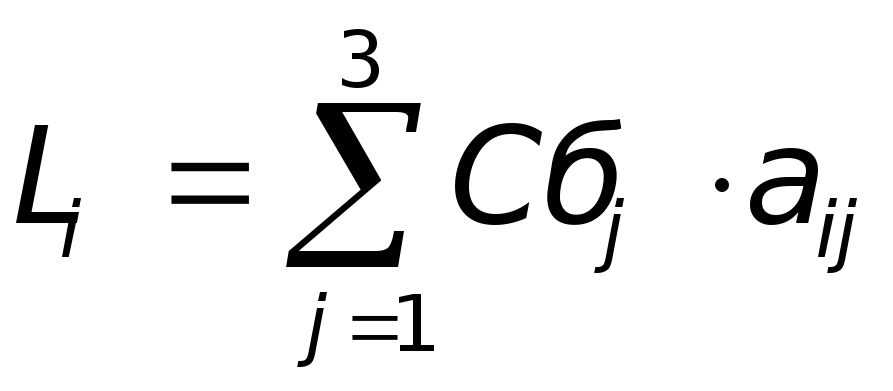 ; ;  ; ;  ; ;  ; ;  ; ;  ; ;  ; ;  ; ;  ; ; |    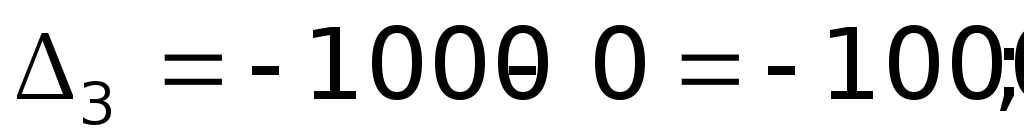   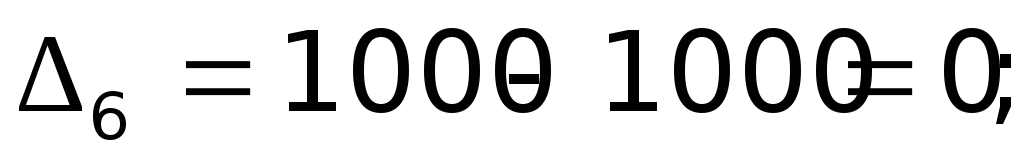   |
Поскольку есть положительные значения ∆, то план не оптимален.
- Находим разрешающий элемент таблицы №1

| Разрешающая строка Разрешающий столбец | Разрешающий элемент |
Максимальное положительное значение имеет 


- Заполняем вторую симплекс таблицу.
- Разрешающую строку делим на разрешающий элемент и записываем на своем месте.
- Обнуляем остальные элементы разрешающего столбца
- Оставшиеся элементы таблицы находим по правилу прямоугольника
где
— Разрешающий элемент.
….
- Рассчитываем опорный план второй таблицы (аналогично первой).

- Для расчета элементов разрешающей строки «=C5/$E$5». Где: С5 – ячейка элемента в предыдущей таблице. $E$5 – ячейка разрешающего элемента с абсолютной адресацией
- Для расчёта свободных элементов по правилу прямоугольника «=($E$5*E4-E$5*$E4)/$E$5». Где: $E$5 – ячейка разрешающего элемента с абсолютной адресацией E4 — ячейка элемента в предыдущей таблице E$5 – ячейка элемента находящегося в одном столбце с искомым элементом и в одной строке с разрешающим элементом. $E4 — ячейка элемента находящегося в одном столбце с разрешающим элементом и в одной строке с искомым элементом.

- Записываем полученный результат в ответ.
Ответ: Оптимальная стоимость дневного рациона составляет 31.6ден. ед. при приобретении 1.6 кг. корма 1-го вида, и 4.2 кг. корма 2-го вида.
Для продолжения скачивания необходимо пройти капчу:
6. Постановка задач линейного программирования. Примеры, различные формы задач и подходы решения. Постановка задач линейного программирования
Линейное программирование — область математики, разрабатывающая теорию и численные методы решения задач нахождения экстремума (максимума или минимума) линейной функции многих переменных при наличии линейных ограничений, т. е. равенств или неравенств, связывающих эти переменные.
В общей постановке задача линейного программирования (ЗЛП) формулируется следующим образом. Имеются какие-то переменные x = (x1, x2,…, xn) и линейная функция этих переменных, которая носит название целевой функции. Ставится задача: найти экстремум (максимум или минимум) целевой функции при условии, что переменные x удовлетворяют системе линейных равенств и/или неравенств.
Функция цели в задаче линейного программирования обычно записывается так:
Или в сокращённом виде с сигмой:
Можно встретить обозначение целевой функции и через C, и через F.
Система ограничений в задаче линейного программирования в канонической форме записывается так:
И система ограничений, и целевая функция имеют линейный характер, то есть содержат переменные только в первой степени.
Целевая функция. Её нужно максимизировать или минимизировать. Для того, чтобы функцию максимизировать, переменные, являющиеся её слагаемыми, должны принимать как можно большие значения в соответствии с условиями задачи. При минимизации — наоборот, меньшие. Обычно целевая функция выражает доходы или расходы.
Переменные. Каждая переменная, как правило, означает запасы одного из производственных факторов — вида сырья, времени, рабочей силы, технологических возможностей или чего-либо другого.
Ограничения. Очень просто. Например, в каждом уравнении (неравенстве) заданы ограничения перечисленных выше или других запасов, используемых для производства определённого вида продукции.
Примеры, различные формы задач и подходы решения
Задача линейного программирования математически может быть представлена в различных формах.
Общей задачей ЛП называется задача, которая состоит в определении максимального (минимального) значения функции
Помимо общей формы, различают еще две частные задачи линейного программирования — стандартную и основную.
Особенностью стандартной задачи ЛП является то, что ее ограничения представлены в виде линейных неравенств, а также условий неотрицательности на переменные, присутствующие в задаче:
Ограничения основной задачи ЛП представляют собой линейные ограничения-равенства, а также условия неотрицательности на переменные:
Задачи линейного программирования в случае двух переменных можно решить и графическим методом, в случаях, когда переменных больше, применяется симплекс-метод.
Примеры решения задач линейного программирования:
Пример №1. Предприятие выпускает продукцию двух разновидностей. Каждый вид продукции проходит обработку на трёх станках. При обработке 1 т продукции I вида первый станок используется 0 ч, второй станок – 1 ч, третий станок – 1 ч. При обработке 1 т продукции II вида первый станок используется 1 ч, второй станок – 4 ч, третий станок – 1 ч. Время работы станков ограничено и не может превышать для первого станка 7 ч, для второго 29 ч, для третьего 11 ч. При реализации 1 т продукции I вида предприятие получает прибыль 2 руб., а при реализации 1 т продукции II вида – 5 руб. Найти оптимальный план выпуска продукции каждого вида, дающий максимальную прибыль от реализации всей продукции.
3. Решим прямую задачу графически:

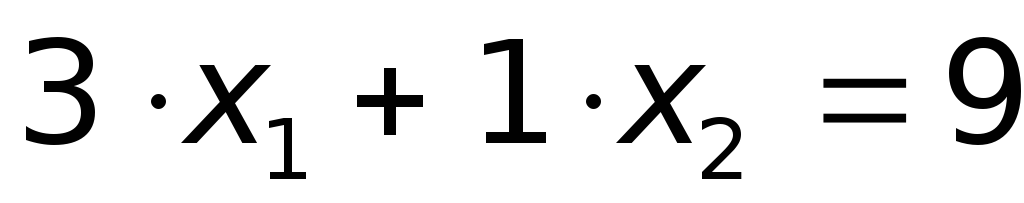 ;
; ,
, Получаем что прямая
Получаем что прямая , заданная уравнением
, заданная уравнением , проходит через точки (3;0) и (2;3);
, проходит через точки (3;0) и (2;3); →Неравенство ошибочно.
→Неравенство ошибочно.
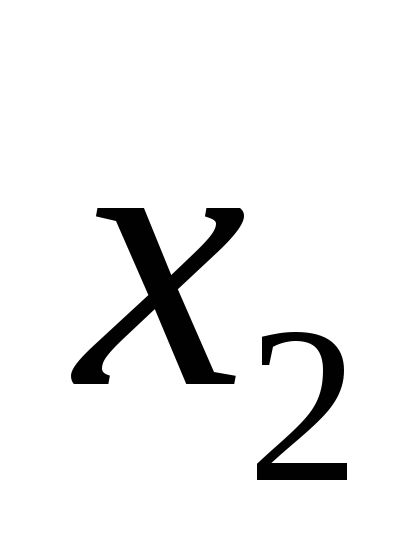 из первого уравнения
из первого уравнения .
. .
. из полученного уравнения
из полученного уравнения


 Полученное значение подставляем в одно из исходных уравнений (первое) и находим
Полученное значение подставляем в одно из исходных уравнений (первое) и находим







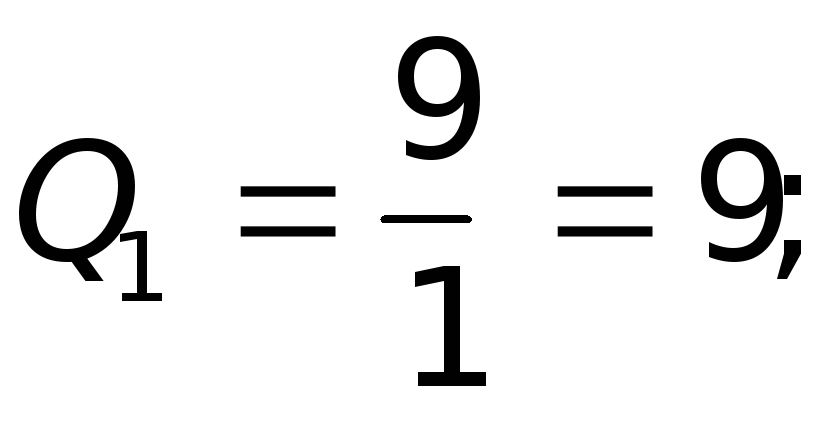

 где
где — Разрешающий элемент.
— Разрешающий элемент. ….
…. Ответ: Оптимальная стоимость дневного рациона составляет 31.6ден. ед. при приобретении 1.6 кг. корма 1-го вида, и 4.2 кг. корма 2-го вида.
Ответ: Оптимальная стоимость дневного рациона составляет 31.6ден. ед. при приобретении 1.6 кг. корма 1-го вида, и 4.2 кг. корма 2-го вида.


