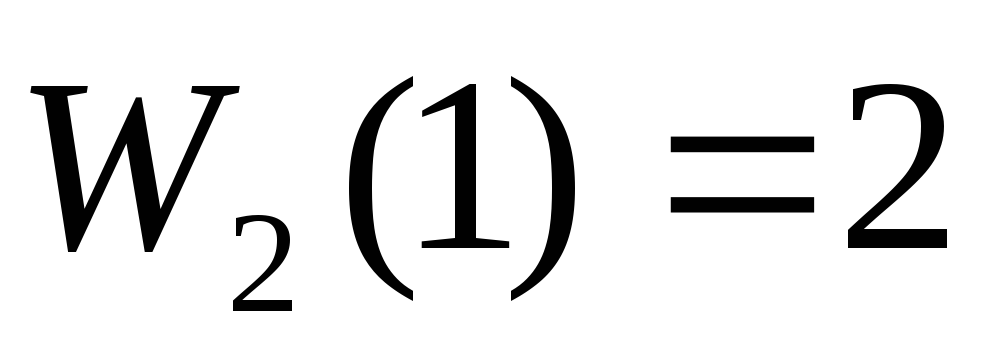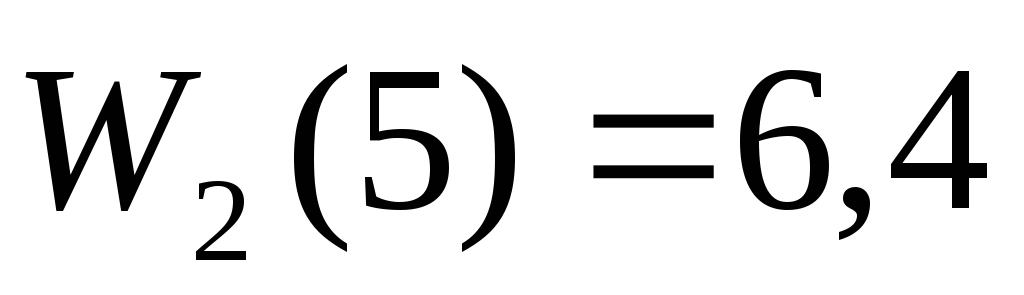Примеры решений задач по динамическому программированию
Задача 1. Для двух предприятий выделено единиц средств. Как распределить все средства в течение 4 лет, чтобы доход был наибольшим, если известно, что доход от единиц средств, вложенных в первое предприятие, равен , а доход от единиц средств, вложенных во второе предприятие, равен . Остаток средств к концу года составляет для первого предприятия и для второго предприятия. Задачу решить методом динамического программирования.
Задача 2. Планируется распределение начальной суммы млн. р. Между четырьмя предприятиями некоторого объединения. Средства выделяются только в размерах кратных млн. р. Функции прироста продукции от вложенных средств на каждом предприятии заданы таблично. Требуется так распределить вложения между предприятиями, чтобы общий прирост продукции (в млн. р.) был максимальным. Решить задачу на основе функционального уравнения Беллмана.
Задача 3. Инвестор выделяет средства в размере 5 тыс. ден. ед., которые должны быть распределены между тремя предприятиями. Требуется, используя принцип оптимальности Беллмана, построить план распределения инвестиций между предприятиями, обеспечивающий наибольшую общую прибыль, если каждое предприятие при инвестировании в него средств x тыс. ден. ед. приносит прибыль pi(x) тыс. ден. ед. (i=1, 2 и 3) по следующим данным (таблица в файле).
Заказать решение
Если вам нужна помощь с решением задач по любым разделам линейного программирования и математическим методам, обращайтесь в МатБюро. Выполняем контрольные и практические работы, ИДЗ и типовые расчеты на заказ. Решаем задания вручную, с помощью Excel, в математических пакетах (Mathcad и другие). Стоимость задания от 150 рублей , оформление производится в Word, срок от 2 дней.
§3. Решение задачи оптимального распределения инвестиций методом динамического программирования
Проиллюстрируем описанную выше процедуру решения задач динамического программирования на следующем примере.
Задача 4.1. Компания выделяет S = 40 млн. руб. для модернизации производства с целью увеличения выпуска продукции. Эти средства следует распределить между тремя филиалами компании. При этом сумма, выделяемая филиалу, должна быть кратна 10 млн. руб.
Известны функции fk(u) (k = ), которые характеризуют прирост выпуска продукции k-го филиала в млн. руб. за год при получении им капиталовложений u млн. руб. (u = 0, 10, 20, 30, 40). Эти данные приведены в таблице 4.1. Нужно найти оптимальный план распределения капиталовложений между филиалами, обеспечивающий максимальный общий годовой прирост выпуска продукции.
Таблица 4.1. Исходная информация к задаче
Размер капитало-вложений (млн. руб.)
Прирост выпуска продукции (млн. руб.)
Решение. Обозначим через uk количество средств, выделенных k-му филиалу, где k = , а Z — общий годовой прирост выпуска продукции. Для нахождения оптимального плана распределения инвестиций следует решить следующую задачу:
uk ≥ 0, k = , (4.3)
Оптимальное решение задачи (4.1) – (4.4) можно найти, сведя ее к задаче линейного целочисленного программирования, аналогично тому, как это было сделано в предыдущей главе (см. задачу 1.3 в §1 главы 7). Другая возможность — использование метода динамического программирования.
Для этого рассмотрим процедуру распределения капиталовложений между филиалами как многошаговый процесс, на k-ом шаге которого выделяются средства k-му филиалу. Таким образом, число шагов этого процесса равно числу филиалов и номер шага соответствует номеру филиала.
Управление uk на k-м шаге (k = ) — это объем средств, выделенных k‑му филиалу, а параметры состояния xk — это остаток капиталовложений после их выделения первым k объектам.
Итак, x0 = 40 — начальный объем капиталовложений, x1 — объем средств, оставшийся после выделения капиталовложений первому филиалу, x2 — объем средств, оставшийся после выделения капиталовложений первому и второму филиалу, а x3 — объем средств, оставшийся после выделения капиталовложений всем трём филиалам.
Уравнения состояния имеют вид:
Множества допустимых управлений на каждом шаге таковы:
Показатель эффективности управления fk(uk) на каждом шаге зависит только от управления на этом шаге и не зависит от предшествующего состояния. Общий показатель эффективности управления имеет вид:
Оптимальное управление доставляет максимум этой функции на множестве допустимых управлений.
В предыдущем параграфе было дано общее описание процедуры нахождения оптимального управления, состоящей из двух этапов: условной и безусловной оптимизации.
Задача оптимального распределения инвестиций
Инструкция . Выберите количество предприятий и количество строк (количество вариантов эффективного вложения), нажмите Далее (см. Пример заполнения). Если доход и остатки предприятий задан в виде функций f(x) и g(x) , задача решается через этот калькулятор.
Пример №1 . Определите оптимальный план расширения производства трех предприятий, если известна их прибыль в год при отсутствии вложений и при инвестировании 1, 2, 3 или 4 млн. Определите, при каком инвестировании будет максимальный процент прироста прибыли.
| f1 | f2 | f3 | xi |
| 40 | 30 | 35 | 0 |
| 90 | 110 | 95 | 1 |
| 395 | 385 | 270 | 2 |
| 440 | 470 | 630 | 3 |
| 620 | 740 | 700 | 4 |
I этап. Условная оптимизация.
1-ый шаг. k = 3.
| e 2 | u 3 | e 3 = e 2 — u 3 | f3(u 3 ) | F*3(e 3 ) | u3(e 3 ) |
| 1 | 0 | 1 | 35 | ||
| 1 | 0 | 95 | 95 | 1 | |
| 2 | 0 | 2 | 35 | ||
| 1 | 1 | 95 | |||
| 2 | 0 | 270 | 270 | 2 | |
| 3 | 0 | 3 | 35 | ||
| 1 | 2 | 95 | |||
| 2 | 1 | 270 | |||
| 3 | 0 | 630 | 630 | 3 | |
| 4 | 0 | 4 | 35 | ||
| 1 | 3 | 95 | |||
| 2 | 2 | 270 | |||
| 3 | 1 | 630 | |||
| 4 | 0 | 700 | 700 | 4 |
2-ый шаг. k = 2.
| e 1 | u 2 | e 2 = e 1 — u 2 | f2(u 2 ) | F*2(e 1 ) | F1(u 2 ,e 1 ) | F*2(e 2 ) | u2(e 2 ) |
| 1 | 0 | 1 | 30 | 95 | 125 | 125 | 0 |
| 1 | 0 | 110 | 0 | 110 | |||
| 2 | 0 | 2 | 30 | 270 | 300 | ||
| 1 | 1 | 110 | 95 | 205 | |||
| 2 | 0 | 385 | 0 | 385 | 385 | 2 | |
| 3 | 0 | 3 | 30 | 630 | 660 | 660 | 0 |
| 1 | 2 | 110 | 270 | 380 | |||
| 2 | 1 | 385 | 95 | 480 | |||
| 3 | 0 | 470 | 0 | 470 | |||
| 4 | 0 | 4 | 30 | 700 | 730 | ||
| 1 | 3 | 110 | 630 | 740 | 740 | 1 | |
| 2 | 2 | 385 | 270 | 655 | |||
| 3 | 1 | 470 | 95 | 565 | |||
| 4 | 0 | 740 | 0 | 740 |
3-ый шаг. k = 1.
| e 0 | u 1 | e 1 = e 0 — u 1 | f1(u 1 ) | F*1(e 0 ) | F0(u 1 ,e 0 ) | F*1(e 1 ) | u1(e 1 ) |
| 1 | 0 | 1 | 40 | 125 | 165 | 165 | 0 |
| 1 | 0 | 90 | 0 | 90 | |||
| 2 | 0 | 2 | 40 | 385 | 425 | 425 | 0 |
| 1 | 1 | 90 | 125 | 215 | |||
| 2 | 0 | 395 | 0 | 395 | |||
| 3 | 0 | 3 | 40 | 660 | 700 | 700 | 0 |
| 1 | 2 | 90 | 385 | 475 | |||
| 2 | 1 | 395 | 125 | 520 | |||
| 3 | 0 | 440 | 0 | 440 | |||
| 4 | 0 | 4 | 40 | 740 | 780 | 780 | 0 |
| 1 | 3 | 90 | 660 | 750 | |||
| 2 | 2 | 395 | 385 | 780 | |||
| 3 | 1 | 440 | 125 | 565 | |||
| 4 | 0 | 620 | 0 | 620 |
Примечание: Столбцы 1 (вложенные средства), 2 (проект) и 3 (остаток средств) для всех трех таблиц одинаковы, поэтому их можно было бы сделать общими. Столбец 4 заполняется на основе исходных данных о функциях дохода, значения в столбце 5 берутся из столбца 7 предыдущей таблицы, столбец 6 заполняется суммой значений столбцов 4 и 5 (в таблице 3-го шага столбцы 5 и 6 отсутствуют).
В столбце 7 записывается максимальное значение предыдущего столбца для фиксированного начального состояния, и в 8 столбце записывается управление из 2 столбца, на котором достигается максимум в 7.
Этап II. Безусловная оптимизация.
Из таблицы 3-го шага имеем F*1(e 0 = 4 млн.руб.) = 780 тыс.руб., то есть максимальная прибыль от инвестирования e 0 = 4 млн.руб. равна 780 тыс.руб.
Из этой же таблицы получаем, что первому предприятию следует выделить u*1(e 0 = 4 млн.руб.) = 0 млн.руб.
При этом остаток средств составит: e 1 = e 0 — u 1 , e 1 = 4 — 0 = 4 млн.руб.
Из таблицы 2-го шага имеем F*2(e 1 = 4 млн.руб.) = 740 тыс.руб., т.е. максимальная прибыль при e 1 = 4 млн.руб. равна 740 тыс.руб.
Из этой же таблицы получаем, что второму предприятию следует выделить u*2(e 1 = 4 млн.руб.) = 1 млн.руб.
При этом остаток средств составит: e 2 = e 1 — u 2 , e 2 = 4 — 1 = 3 млн.руб.
Последнему предприятию достается 3 млн.руб. Итак, инвестиции в размере 4 млн.руб. необходимо распределить следующим образом: первому предприятию ничего не выделять, второму предприятию выделить 1 млн.руб., третьему предприятию выделить 3 млн.руб., что обеспечит максимальную прибыль, равную 780 тыс.руб.
Пример №2 . Имеются 4 предприятия, между которыми необходимо распределить 100 тыс. усл. ед. средств. Значения прироста выпуска продукции на предприятии в зависимости от выделенных средств Х представлены в таблице. Составить оптимальный план распределения средств, позволяющий максимизировать общий прирост выпуска продукции.
5.5. Оптимальное распределение инвестиций как задача динамического программирования
Инвестор выделяет средства в размере 





Выигрышем W данной задаче является прибыль, приносимая -предприятиями.
Построение математической модели.
- Определение числа шагов. Число шагов т равно числу предприятий, в которые осуществляется инвестирование.
- Определение состояний системы. Состояние системы на каждом шаге характеризуется количеством средств
, имеющихся в наличии перед данным шагом,
.
- Выбор шаговых управлений. Управлением на
-м шаге
,
является количество средств, инвестируемых в
-е предприятие.
- Функция выигрыша на
-м шаге



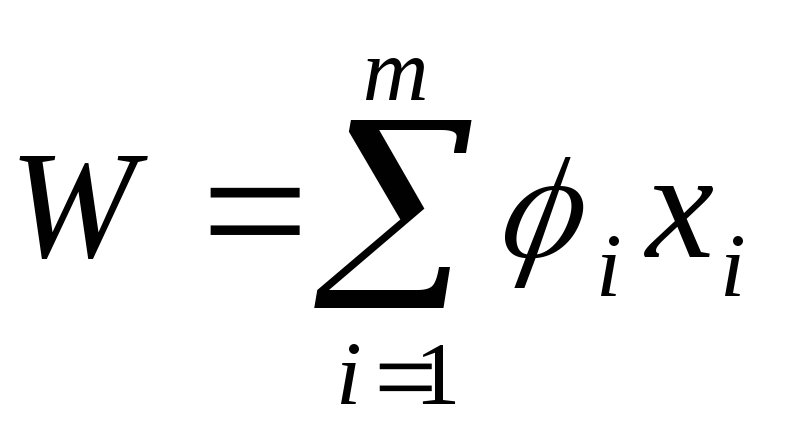






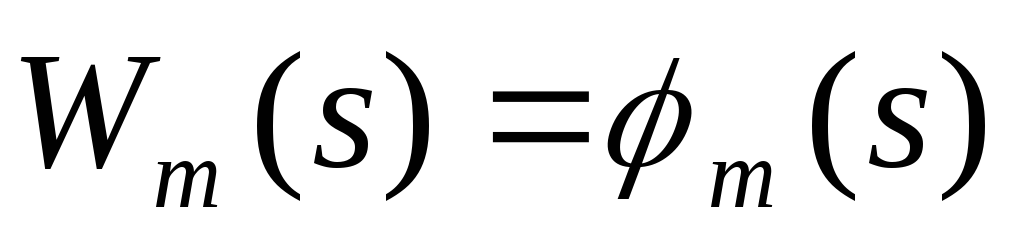













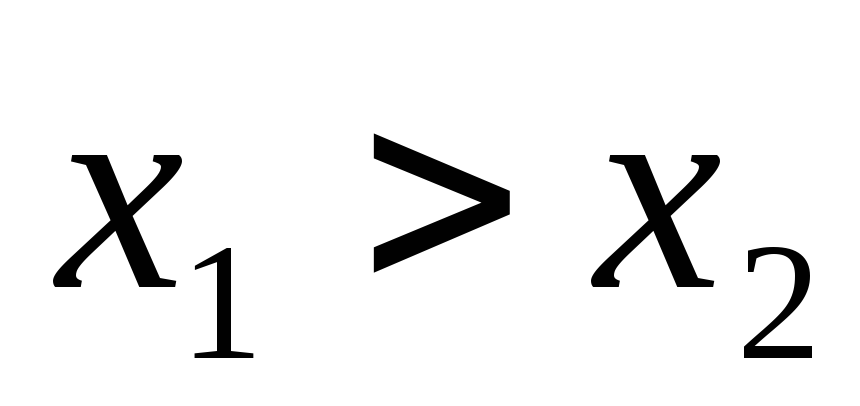







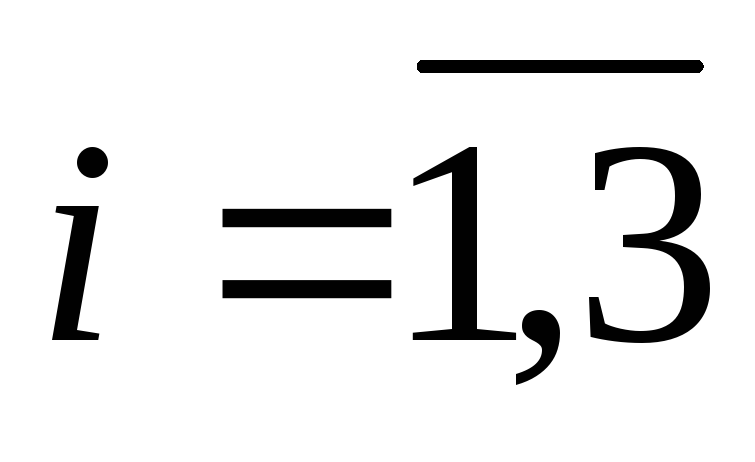





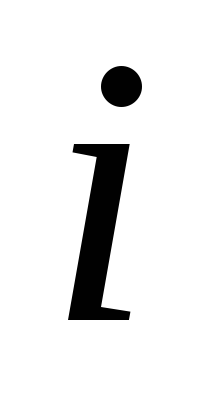
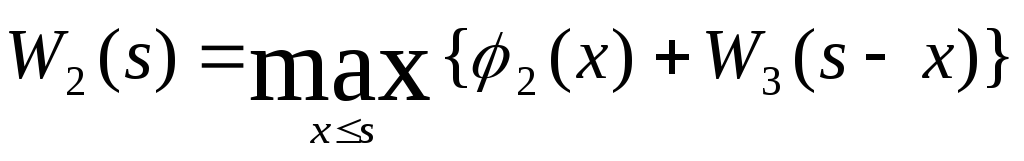

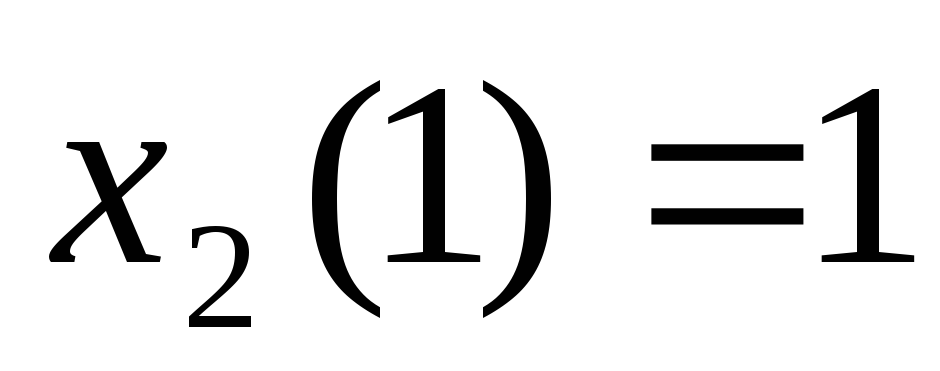



















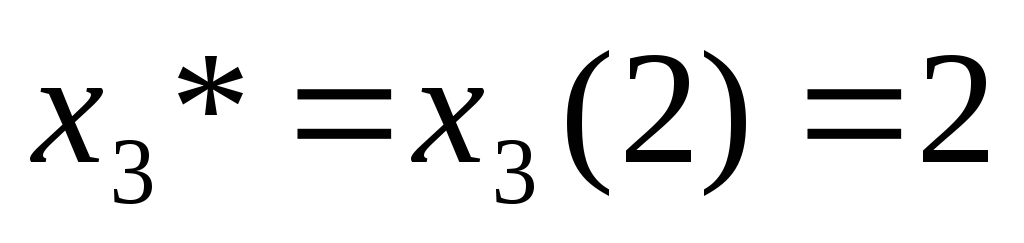



 , имеющихся в наличии перед данным шагом,
, имеющихся в наличии перед данным шагом, .
. -м шаге
-м шаге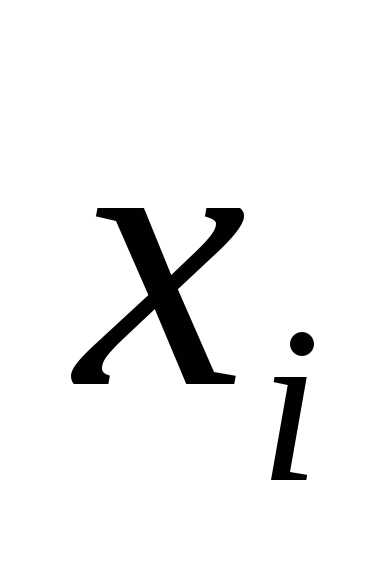 ,
, является количество средств, инвестируемых в
является количество средств, инвестируемых в -е предприятие.
-е предприятие. -м шаге
-м шаге