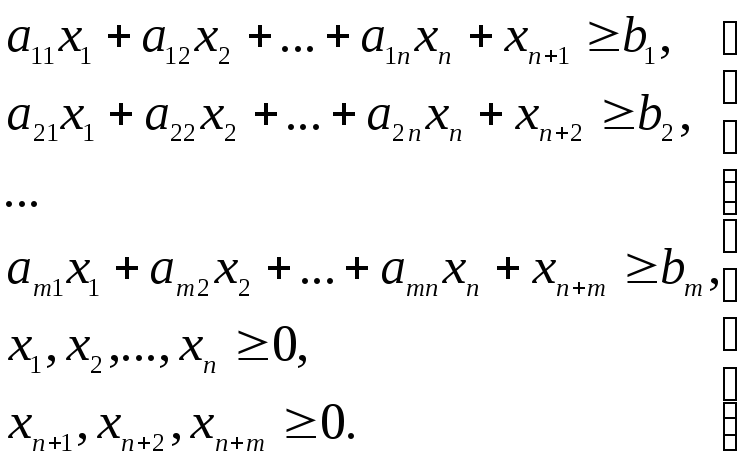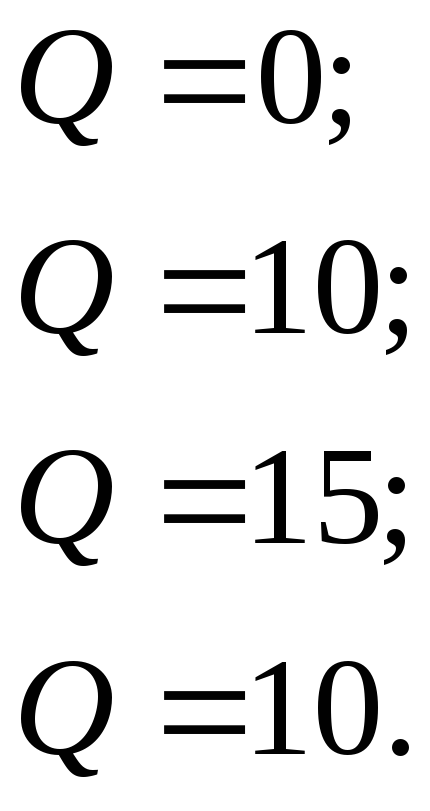Решение задачи линейного программирования при ограничениях имеет вид

Решение задач линейного программирования

Назначение сервиса . Онлайн-калькулятор предназначен для решения задач линейного программирования симплексным методом путем перехода к КЗЛП и СЗЛП . При этом задача на минимум целевой функции сводятся к задаче на поиск максимума через преобразование целевой функции F*(X) = -F(X) . Также имеется возможность составить двойственную задачу.

1. Переход к КЗЛП. Любая ЗЛП вида ax ≤ b , ax ≥ b , ax = b ( F(X) → extr ) сводится к виду ax = b , F(X) → max ;
2. Переход к СЗЛП. КЗЛП вида ax = b сводится к виду ax ≤ b , F(X) → max ;
3. Решение симплексным методом;

• Шаг №1
• Шаг №2
• Видеоинструкция
• Оформление Word

Инструкция . Выберите количество переменных и количество строк (количество ограничений). Полученное решение сохраняется в файле Word .

Переход от задачи минимизации целевой функции к задаче максимизации

Задача минимизации целевой функции F(X) легко может быть сведена к задаче максимизации функции F*(X) при тех же ограничениях путем введения функции: F*(X) = -F(X) . Обе задачи имеют одно и то же решение X*, и при этом min(F(X)) = -max(F*(X)) .
Проиллюстрируем этот факт графически:

F(x) → min

F(x) → max

Для оптимизации функции цели используем следующие понятия и методы.
Опорный план – план с определёнными через свободные базисными переменными.
Базисный план – опорный план с нулевыми базисными переменными.
Оптимальный план – базисный план, удовлетворяющий оптимальной функции цели (ФЦ).

Ведущий (разрешающий) элемент – коэффициент свободной неизвестной, которая становится базисной, а сам коэффициент преобразуется в единицу.
Направляющая строка – строка ведущего элемента, в которой расположена с единичным коэффициентом базисная неизвестная, исключаемая при преобразовании (строка с минимальным предельным коэффициентом, см. далее).
Направляющий столбец – столбец ведущего элемента, свободная неизвестная которого переводится в базисную (столбец с максимальной выгодой, см. далее).

Переменные x₁, …, x_m, входящие с единичными коэффициентами только в одно уравнение системы, с нулевыми – в остальные, называются базисными или зависимыми. В канонической системе каждому уравнению соответствует ровно одна базисная переменная. Переход осуществляется с помощью метода Гаусса–Жордана. Основная идея этого метода состоит в сведении системы m уравнений с n неизвестными к каноническому виду при помощи элементарных операций над строками.
Остальные n-m переменных (x_m+1,…, x_n) называются небазисными или независимыми переменными.

Базисное решение называется допустимым базисным решением, если значения входящих в него базисных переменных x_j≥0, что эквивалентно условию неотрицательности b_j≥0.
Допустимое базисное решение является угловой точкой допустимого множества S задачи линейного программирования и называется иногда опорным планом.
Если среди неотрицательных чисел b_j есть равные нулю, то допустимое базисное решение называется вырожденным (вырожденной угловой точкой) и соответствующая задача линейного программирования называется вырожденной.

Пример №1 . Свести задачу линейного программирования к стандартной ЗЛП.
F(X) = x₁ + 2x₂ — 2x₃ → min при ограничениях:
4x₁ + 3x₂ — x₃≤10
— 2x₂ + 5x₃≥3
x₁ + 2x₃=9
Для приведения ЗЛП к канонической форме необходимо:
1. Поменять знак у целевой функции. Сведем задачу F(X) → min к задаче F(X) → max. Для этого умножаем F(X) на (-1). В первом неравенстве смысла (≤) вводим базисную переменную x₄; во втором неравенстве смысла (≥) вводим базисную переменную x₅ со знаком минус.
4x₁ + 3x₂-1x₃ + 1x₄ + 0x₅ = 10
0x₁-2x₂ + 5x₃ + 0x₄-1x₅ = 3
1x₁ + 0x₂ + 2x₃ + 0x₄ + 0x₅ = 9
F(X) = — x₁ — 2x₂ + 2x₃
Переход к СЗЛП.
Расширенная матрица системы ограничений-равенств данной задачи:

4	3	-1	1	0	10
0	-2	5	0	-1	3
1	0	2	0	0	9

Приведем систему к единичной матрице методом жордановских преобразований.
1. В качестве базовой переменной можно выбрать x₄.
2. В качестве базовой переменной выбираем x₂.
Разрешающий элемент РЭ=-2. Строка, соответствующая переменной x₂, получена в результате деления всех элементов строки x₂ на разрешающий элемент РЭ=-2. На месте разрешающего элемента получаем 1. В остальных клетках столбца x₂ записываем нули. Все остальные элементы определяются по правилу прямоугольника. Представим расчет каждого элемента в виде таблицы:

4-(0 • 3):-2	3-(-2 • 3):-2	-1-(5 • 3):-2	1-(0 • 3):-2	0-(-1 • 3):-2	10-(3 • 3):-2
0 : -2	-2 : -2	5 : -2	0 : -2	-1 : -2	3 : -2
1-(0 • 0):-2	0-(-2 • 0):-2	2-(5 • 0):-2	0-(0 • 0):-2	0-(-1 • 0):-2	9-(3 • 0):-2

Получаем новую матрицу:

4	0	6 1 /2	1	-1 1 /2	14 1 /2
0	1	-2 1 /2	0	1 /2	-1 1 /2
1	0	2	0	0	9

3. В качестве базовой переменной выбираем x₃.
Разрешающий элемент РЭ=2. Строка, соответствующая переменной x₃, получена в результате деления всех элементов строки x₃ на разрешающий элемент РЭ=2. На месте разрешающего элемента получаем 1. В остальных клетках столбца x₃ записываем нули. Все остальные элементы определяются по правилу прямоугольника. Представим расчет каждого элемента в виде таблицы:

4-(1 • 6 1 /2):2	0-(0 • 6 1 /2):2	6 1 /2-(2 • 6 1 /2):2	1-(0 • 6 1 /2):2	-1 1 /2-(0 • 6 1 /2):2	14 1 /2-(9 • 6 1 /2):2
0-(1 • -2 1 /2):2	1-(0 • -2 1 /2):2	-2 1 /2-(2 • -2 1 /2):2	0-(0 • -2 1 /2):2	1 /2-(0 • -2 1 /2):2	-1 1 /2-(9 • -2 1 /2):2
1 : 2	0 : 2	2 : 2	0 : 2	0 : 2	9 : 2

Получаем новую матрицу:

3 /4	0	0	1	-1 1 /2	-14 3 /4
1 1 /4	1	0	0	1 /2	9 3 /4
1 /2	0	1	0	0	4 1 /2

Поскольку в системе имеется единичная матрица, то в качестве базисных переменных принимаем X = (4,2,3).
Соответствующие уравнения имеют вид:
3 /₄x₁ + x₄ — 1 1 /₂x₅ = -14 3 /₄
1 1 /₄x₁ + x₂ + 1 /₂x₅ = 9 3 /₄
1 /₂x₁ + x₃ = 4 1 /₂
Выразим базисные переменные через остальные:
x₄ = — 3 /₄x₁ + 1 1 /₂x₅-14 3 /₄
x₂ = — 1 1 /₄x₁ — 1 /₂x₅+9 3 /₄
x₃ = — 1 /₂x₁+4 1 /₂
Подставим их в целевую функцию:
F(X) = — x₁ — 2(- 1 1 /₄x₁ — 1 /₂x₅+9 3 /₄) + 2(- 1 /₂x₁+4 1 /₂)
или
F(X) = 1 /₂x₁ + x₅-10 1 /₂ → max
Система неравенств:
— 3 /₄x₁ + 1 1 /₂x₅-14 3 /₄ ≥ 0
— 1 1 /₄x₁ — 1 /₂x₅+9 3 /₄ ≥ 0
— 1 /₂x₁+4 1 /₂ ≥ 0
Приводим систему неравенств к следующему виду:
3 /₄x₁ — 1 1 /₂x₅ ≤ -14 3 /₄
1 1 /₄x₁ + 1 /₂x₅ ≤ 9 3 /₄
1 /₂x₁ ≤ 4 1 /₂
F(X) = 1 /₂x₁ + x₅-10 1 /₂ → max
Упростим систему.
3 /₄x₁ — 1 1 /₂x₂ ≤ -14 3 /₄
1 1 /₄x₁ + 1 /₂x₂ ≤ 9 3 /₄
1 /₂x₁ ≤ 4 1 /₂
F(X) = 1 /₂x₁ + x₂-10 1 /₂ → max

Источник

2. Линейное программирование

К задачам линейного программирования относятся такие оптимизационные задачи, в которых и целевая функция и ограничения – линейный многочлен.

2.1. Стандартный вид задачи линейного программирования (злп)

В стандартном виде ЗЛП целевая функция минимизируется, ограничения имеют вид равенств:

(2.1)

Здесь a_ij, b_i, p_i – постоянные коэффициенты.

В этих задачах количество переменных больше или равно количеству ограничений-равенств: n≥m.

Если n  m, то область допустимых решений – точка;

если n  m, то область допустимых решений – многогранник;

если n  m, то (m – n) ограничений линейно зависимы и их можно исключить.

2.2. Способы приведения задачи линейного программирования к стандартному виду

Случай 1. Исходные условия задачи: целевая функция минимизируется, ограничения представляют систему неравенств вида «меньше или равно».

Для приведения задачи к стандартному виду вводят искусственные переменные . Эти искусственные переменные прибавляют к левым частям ограничений:

(2.2)

Полученная задача тождественна исходной. Действительно, убрав искусственные переменные, получим левые части ограничений  b_i.

Случай 2. Исходные условия задачи: целевая функция минимизируется, ограничения имеют вид неравенств типа «больше или равно»:

Аналогично предыдущему случаю вводятся искусственные переменные, но эти переменные вычитаются из левых частей ограничений.

Случай 3. Исходные условия задачи: целевая функция максимизируется, ограничения имеют вид равенств.

Для приведения задачи к стандартному виду (2.1) сменим целевую функцию на целевую функциюG, все коэффициенты которой помножены на –1: Полученная задача тождественна исходной.

2.3. Графический метод решения задач линейного программирования

Графический метод применяется для решения задач небольшой размерности (количество переменных не превышает 3). Рассмотрим метод на примере решения следующей задачи:

(2.3)

1. Ограничения-неравенства заменяются на ограничения-равенст­ва:

1. Строятся графики полученных функций:

Рис. 2.1. Графический метод решения ЗЛП

1. Находится область допустимых решений (область, где выполняются все ограничения).
2. Строится график целевой функции при каком-либо значении правой части:

1. График целевой функции перемещается параллельно самому себе в сторону роста (уменьшения при Q  min) целевой функции до касания с границей области допустимых решений. Граничная точка (или отрезок прямой) является решением задачи линейного программирования.
2. Находится решение: координаты граничной точки (точка А) и значение целевой функции в этой точке:

Выводы: 1. Область допустимых решений задачи линейного программирования представляет собой выпуклый многогранник. 2. Решение задачи линейного программирования находится на границе области допустимых решений. Способ 2. Пункты 1–3 выполняются аналогично Способу 1.

1. Подсчитываются значения целевой функции во всех вершинах допустимого многогранника.

, следовательно, точка – решение задачи. Пример 1. Способ 1.

1. Ограничения-неравенства заменяются на ограничения-равенства:

1. Строятся графики полученных функций:

Рис. 2.2. 3. Находится область допустимых решений (область, где выполняются все ограничения). 4. Строится график целевой функции при каком-либо значении правой части: 5. График целевой функции перемещается параллельно его начальному положению в сторону уменьшения целевой функции до касания с границей области допустимых решений. Отрезок прямой АВ является решением задачи линейного программирования. 6. В ответе записываются функция, граничные точки отрезка и значение целевой функции на этом отрезке: , , Способ 2. 1 – 3 пункты выполняются аналогично Способу 1.

1. Подсчитываются значения целевой функции во всех вершинах допустимого многогранника.

–в двух точках, следовательно, отрезок AB, соединяющий эти точки, является решением задачи.

Источник