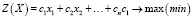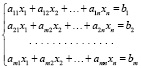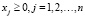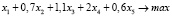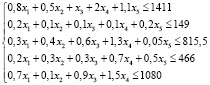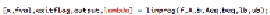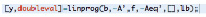Решение задачи линейного программирования матлаб
Настоящая статья посвящена разбору использования среды программирования MatLab при решении задач линейного программирования. Идея статьи возникла при обсуждении преподавания дисциплины «Линейная алгебра». Квалифицированный специалист должен довольно неплохо разбираться не только в методах решения задач, но и уметь проанализировать полученные результаты. Многочисленные математические пакеты и программы позволяют это сделать довольно легко и быстро. Мы предлагаем на примере одного такого пакета MatLab рассмотреть решение задач линейного программирования и с его помощью сделать анализ полученного результата. Были написаны алгоритмы, позволяющие разрешать задачи линейной оптимизации. Данный код позволяет продемонстрировать практическое применение теоретического подхода на современных вычислительных системах, раскрывая смысл каждого показателя. Была разобрана задача-пример, решенная при помощи данного кода.
2. Маслякова И.Н. Применение процедуры Байесовского оценивания в последовательности тестов при подготовке специалистов // European researcher. Series A. – 2011. – № 5–1. – С. 509–510.
3. Маслякова И.Н., Мочалина Е.П., Татарников О.В., Иванкова Г.Н. Модель рекуррентного оценивания уровня знаний студента // Менеджмент и бизнес-администрирование. – 2015. – № 3. – С. 71–76.
4. Титов В.А., Долгополов А.А. Применение симплекс-метода для решения задач динамического управления запасами организации // Современные проблемы науки и образования. – 2014. – № 3; URL: http://www.science-education.ru/ru/article/view Титов В.А., Долгополов А.А. Линейные математические модели управления запасами производственной компании с учетом фактора времени // Успехи современного естествознания. – 2015. – № 1–1. – С. 170–171.
6. Титов В.А., Максимов Д.А. Методы оценки экономической безопасности производственной сферы интегрированной производственной структуры // Путеводитель предпринимателя. – 2013. – № 18. – С. 188–205.
Еще в XIX в. общество начало предпринимать первые попытки составить математическую модель экономических проблем для создания точных прогнозов и принятия оптимальных решений. В 1939 г. советский математик Л.В. Канторович опубликовал работу «Математические методы организации и планирования производства», в которой заложил основы линейного программирования. Сам термин был предложен в середине 1940-х гг. американским математиком Джорджем Бернардом Данцигом, автором симплекс-метода [1]. В те времена вычислительная техника пребывала в самом начале своего развития, поэтому симплекс-таблицы, содержащие большое количество переменных, требовали большого количества ресурсов. С развитием IT-технологий, и в особенности появлением персональных компьютеров, исчезла проблема большого количества переменных при решении задач математического программирования. Но появилась другая проблема – проблема использования IT-технологий при подготовке специалистов. Ни для кого не секрет, что во многих российских вузах при подготовке экономистов практически не используются современные математические пакеты и программы для решения тех или иных задач. А это, в свою очередь, снижает конкурентоспособность нашего образования, а экономика нашей страны недополучает высококвалифицированных специалистов [3].
Идея написания данной работы возникла при изучении раздела линейной алгебры «Линейное программирование». Одним из достоинств, но и в то же время недостатков нашего образования является фундаментальность и теоретизированность подачи материала. На наш взгляд, необходим баланс между фундаментальной теорией, решением практических задач и применением современных технологий [2]. В данной работе продемонстрирован такой подход на примере решения задачи линейного программирования и ее постоптимального анализа.
Целью данной работы является создание универсального инструмента на базе среды Matlab для работы с задачами постоптимального анализа, который за счёт своей открытости не только может легко быть перестроен под специализированные задачи, но и стать иллюстрацией методов данного вида анализа экономических задач. Студенты смогут легко проследить, а следовательно, и понять, каким образом при изменении базисных переменных меняется значение целевой функции.
Общая постановка задачи оптимизации
В ходе решения задачи оптимизации необходимо будет выполнить следующие этапы решения:
- Получить оптимальный план прямой задачи
- Определить дефицитные ресурсы
- Получить оптимальный план двойственной задачи
- Найти интервалы устойчивости ресурсов
- Предоставить данные пользователю
Постановка и решение прямой задачи линейного программирования
Общей задачей линейного программирования является задача, которая состоит в определении максимального или же минимального значения целевой функции при заданной системе ограничений (рис. 1).
Рис. 1. Общий вид задачи линейного программирования
К данным задачам сводятся многочисленные задачи экономического содержания [5]. Для решения этих задач в среде Matlab используется функция linprog из дополнения OptimizationToolbox. Работа с данной функцией производится путём задания пользователем данных о задаче следующими условиями:
Таким образом, для нахождения оптимального решения прямой задачи следует обратиться к функции в форме
[x, fval] = linprog (f, A, b, Aeq, beq, lb, ub)После выполнения данной функции, в массиве x будут находиться значения аргументов функции для оптимального решения, а переменная fval будет равна значению целевой функции при данных значениях.
Приведем пример решения задачи:
Рис. 2. Система ограничений примера
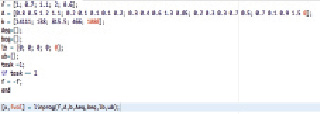
Соответственно, на экране данная задача будет выглядеть так:
Рис. 3. Запись системы ограничений примера в среде MatLab и нахождение решения
Здесь task = 1 (переменная-маркер поиска максимума/минимума целевой функции).
Значения в x на выходе будут:
При выполнении данной функции также можно сразу же получить значения теневых цен ресурсов, заменив запись на:
Рис. 4. Вызов функции с введением дополнительных аргументов для получения теневых цен
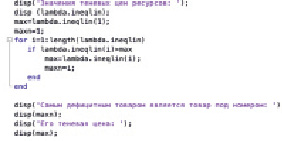
Рис. 5. Автоматизированный поиск наиболее дефицитного товара
В таком случае (рис. 4) в матрице lambda.ineqlin будут содержаться значения множителей Лагранжа для данной задачи. По своему экономическому смыслу множители Лагранжа одинаковы с теневыми ценами, которые показывают, насколько дефицитным является товар [6].
Код, представленный на рис. 5, показывает, как на основании полученных значений в матрице lambda.ineqlin определить наиболее дефицитный товар и его теневую цену. В теле цикла в переменной max содержится последнее известное максимальное значение, а в maxn – его порядковый номер.
Составление двойственной задачи линейного программирования
Рис. 6. Взаимосвязь коэффициентов прямой и двойственной задач
Двойственную задачу к любой прямой задаче можно вывести, руководствуясь данными правилами:
- Если прямая задача является задачей максимизации, то двойственная будет задачей минимизации, и наоборот.
- Каждому ограничению типа стандартного неравенства прямой задачи соответствует неотрицательная двойственная переменная двойственной задачи, и наоборот.
- Каждому ограничению типа равенства прямой задачи соответствует двойственная переменная без ограничения на знак, и наоборот.
- Коэффициенты целевой функции прямой задачи становятся свободными членами ограничений двойственной задачи, и наоборот.
- Матрицу ограничений двойственной задачи получают транспонированием матрицы ограничений прямой задачи.
Рис. 7. Код для решения двойственной задачи на основе заданных коэффициентов прямой задачи
В коде (рис. 7) используется тот же метод linprog, однако меняются аргументы функции в соответствии с теорией. В матрице y будут находиться значения неизвестных двойственной задачи, а в переменной doubleval – значение целевой функции двойственной задачи.
Нахождение интервалов устойчивости ресурсов
Для нахождения интервалов устойчивости ресурсов будем изменять количество каждого из ресурсов поочередно с заданным шагом до момента, когда решение перестанет быть оптимальным. Для этого будем, изменив значение свободного члена ограничений, сверять значения в матрице оптимальных оценок с изначальной матрицей оптимальных оценок.
Рис. 8. Код для нахождения нижней границы устойчивости ресурсов
Представленный на рис. 8 код для нахождения нижней границы устойчивости ресурсов легко можно использовать для установления верхней границы устойчивости, заменив операцию вычитания на операцию сложения. Смысл данного алгоритма состоит в том, что при изменении значения какого-либо ресурса в пределах его интервала устойчивости, значение целевой функции не изменяется. В переменной approxim задаётся значение приближения, чем оно меньше – тем точнее получаемый результат, однако медленнее вычисления. Таким образом, каждый раз, когда мы изменяем значение какого-то из ресурсов на значение переменной approxim, мы сравниваем его со значением целевой функции при начальных условиях. Как только значения перестают совпадать – обнаруживает себя граница интервала устойчивости, и данную процедуру можно повторять для следующего ресурса [4].
Среда Matlab – крайне гибкий инструмент. Её использование в задачах оптимизации позволяет создать не просто приложение, но и наглядное пособие при обучении работе с задачами линейного программирования. На основании составленного «каркаса» возможно изменение используемых алгоритмов, подстройка кода под определенную задачу, а также настройка работы с большими данными, оформленными в форматах текстов файлов или записей БД. Заметим, что это только первый шаг на пути к созданию нового подхода в преподавании математических дисциплин.
Решение задач линейного программирования в Matlab
На просторах интернета полно пример работы с командой linprog, которая позволяет решать задачи линейного программирования в Matlab. Да вот беда. Нигде не показано как ей пользоваться в полном объеме. Куча примеров простейшего уравнения, да и только.
Давайте рассмотрим такой пример:
5×1 — 2×2 + x3 >= 3
-2×1 + 3×2 — 2×3 x1 + x2 + x3 = 9
1 2 x3 >= 1
f = x1 + x2 — 2×3
Как видите в данном примере есть и равенство и ограничения нижнего/верхнего значений переменных. И все это нужно куда то задавать.
Сперва зададим матрицу целевой функции:
Теперь зададим матрицу коэффициентов неравенств. При этом все неравенства должны быть приведены к виду «меньше или равно». Если это не так, то меняем знаки.
Дальше задаем знаки правой части неравенств:
Задаем нижние ограничения переменных из двойных неравенств:
Задаем верхние ограничения из двойных неравенств:
[x,fval,exitflag,output,lambda] = linprog(f,A,b,Aeq,Beq,lb,ub)
Optimization terminated. x = 1.0000 2.0000 6.0000 fval = -9.0000 exitflag = 1 output = iterations: 6 algorithm: 'interior-point' cgiterations: 0 message: 'Optimization terminated.' constrviolation: 3.6149e-12 firstorderopt: 7.2028e-11 lambda = ineqlin: [3x1 double] eqlin: 2.0000 upper: [3x1 double] lower: [3x1 double]
Так мы нашли минимум. Для нахождения максимума целевой функции необходимо сменить знаки в массиве f и повторить расчет.
Похожий код:
Программист, разработчик с 5 летним опытом работы. Учусь на разработчика игр на Unity и разработчика VR&AR реальности (виртуальной реальности). Основные языки программирования: C#, C++.