Решение задач программирование блок схема

Решение задач программирование блок схема

Усвоить понятия: алгоритм как фундаментальное понятие информатики, способы описания, основные типы алгоритмов, освоить принципы решения задач с использованием основных алгоритмических конструкций.

Задачи лабораторной работы

• знать назначение алгоритма и его определение;
• знать формы представления алгоритма;
• уметь работать с основными алгоритмическими конструкциями;
• уметь представлять алгоритм в виде блок-схемы;
• уметь приводить примеры алгоритмов и применять их для построения блок-схем;
• уметь составлять и записывать алгоритм одним из способов.

Перечень обеспечивающих средств

Общие теоретические сведения

Решение любой задачи на ЭВМ можно разбить на следующие этапы: разработка алгоритма решения задачи, составление программы решения задачи на алгоритмическом языке, ввод программы в ЭВМ, отладка программы (исправление ошибок), выполнение программы на ПК, анализ полученных результатов.

Алгоритм – это точная конечная система правил, определяющая содержание и порядок действий исполнителя над некоторыми объектами (исходными и промежуточными данными) для получения после конечного числа шагов искомого результата.

• словесным (пример в начале раздела);
• графическим (виде специальной блок-схемы);
• с помощью специальных языков программирования.

Блок-схема – распространенный тип схем, описывающий алгоритмы или процессы, изображая шаги в виде блоков различной формы, соединенных между собой стрелками.

1. Линейный алгоритм – это такой алгоритм, в котором все операции выполняются последовательно одна за другой.
2. Алгоритмы разветвленной структуры применяются, когда в зависимости от некоторого условия необходимо выполнить либо одно, либо другое действие.
3. Алгоритмы циклической структуры .

Циклом называют повторение одних и тех же действий (шагов). Последовательность действий, которые повторяются в цикле, называют телом цикла .

Циклические алгоритмы подразделяют на алгоритмы с предусловием, постусловием и алгоритмы с конечным числом повторов. В алгоритмах с предусловием сначала выполняется проверка условия окончания цикла и затем, в зависимости от результата проверки, выполняется (или не выполняется) так называемое тело цикла.

Источник

1. Практическая работа Разработка блок-схемы алгоритма решения задачи

Цель работы: изучение графического способа описания алгоритма решения задачи.

• ознакомиться с основными способами представления алгоритмов;
• освоить графический способ описания алгоритмов.

1.1. Порядок выполнения работы

1. Изучите теоретические сведения по теме данного раздела (п. 1.2)
2. Ознакомьтесь с постановкой задачи (п. 1.3). Вариант задания соответствует вашему номеру в списке группы.
3. Разработайте блок-схему алгоритма решения поставленной задачи.
4. Ответьте на контрольные вопросы.
5. Подготовьте отчет о выполнении практической работы, который должен содержать:

• титульный лист;
• цель практической работы;
• блок-схему алгоритма решения поставленной задачи;
• ответы на контрольные вопросы;
• выводы по практической работе.

1.2. Общие сведения

Одним из наиболее трудоемких этапов решения задачи на ЭВМ является разработка алгоритма.

Под алгоритмом понимается точное предписание, определяющее вычислительный процесс, ведущий от варьируемых начальных данных к искомому результату.

Основными характерными свойствами алгоритма являются:

1. детерминированность (определенность) – при заданных исходных данных обеспечивается однозначность искомого результата;
2. массовость – пригодность для задач данного типа при исходных данных, принадлежащих заданному подмножеству;
3. результативность – реализуемый вычислительный процесс выполняется за конечное число этапов с выдачей осмысленного результата;
4. дискретность – возможность разбиения алгоритма на отдельные этапы, выполнение которых не вызывает сомнений.

Выделяют следующие типы вычислительных процессов:

Для получения результата необходимо выполнить некоторые операции в определенной последовательности.

Конкретная последовательность операций зависит от значений одного или нескольких параметров. Например, если дискриминант квадратного уравнения не отрицателен, то уравнение имеет два корня, а если отрицателен, то действительных корней нет.

Для получения результата некоторую последовательность действий необходимо выполнить несколько раз. Например, для того, чтобы получить таблицу значений функции на заданном интервале изменения аргумента с заданным шагом, необходимо соответствующее количество раз определить следующее значение аргумента и посчитать для него значение функции.

В свою очередь, существуют также несколько типов циклического вычислительного процесса, а именно:

1. Счетные циклы (циклы с заданным количеством повторений) – ­­ это циклические процессы, для которых количество повторений известно.
2. Итерационные циклы – это циклические процессы, завершающиеся по достижении или нарушении некоторых условий.
3. Поисковые циклы – это циклические процессы, из которых возможны два варианта выхода:

— выход по завершению процесса;

— досрочный выход по какому-либо дополнительному условию.

По типу вычислительного процесса, реализуемого алгоритмом, различают:

— алгоритмы линейной структуры;

— алгоритмы разветвленной структуры;

— алгоритмы циклической структуры.

Алгоритмы решения практических задач обычно имеют комбинированную структуру, то есть включают в себя все три типа вычислительных процессов.

К изобразительным средствам описания алгоритмов относятся следующие основные способы их представления:

— словесный ( записи на естественном языке);

— структурно-стилизованный (записи на алгоритмическом языке и псевдокод);

— графический ( изображение схем и графических символов);

— программный (тексты на языках программирования).

Словесный способ описания алгоритма представляет собой описание последовательных пронумерованных этапов обработки данных и задается в произвольном изложении на естественном языке.

Алгоритм сложения двух чисел (a и b).

1. Спросить, чему равно число a.
2. Спросить, чему равно число b.
3. Сложить a и b, результат присвоить с.
4. Сообщить результат с.

Достоинством данного способа является простота описания, а к недостаткам можно отнести то, что такой подход многословен и не имеет строгой формализации, поэтому допускает неоднозначность толкования отдельных предписаний, в силу чего словесный способ представления алгоритма не имеет широкого распространения.

Для строгого задания различных структур данных и алгоритмов их обработки требуется иметь такую систему формальных обозначений и правил, чтобы смысл всякого используемого предписания трактовался точно и однозначно. Соответствующие системы правил называются языками описаний. К ним относятся алгоритмические языки (псевдокоды), блок-схемы и языки программирования.

Структурно-стилизованный способ описания алгоритма основан на записи алгоритмов в формализованном представлении предписаний, задаваемых путем использования ограниченного набора типовых синтаксических конструкций, называемых часто псевдокодами.

Достоинством псевдокодов является близость к языкам программирования, а недостатками, в свою очередь, являются сложность освоения и невозможность непосредственного ввода алгоритма для решения на ЭВМ, т.е. необходимость перевода на язык программирования.

Графический способ описания алгоритма предполагает, что для описания структуры алгоритма используется совокупность графических изображений (блоков), соединяемых линиями передачи управления. Такое изображение называется методом блок-схем.

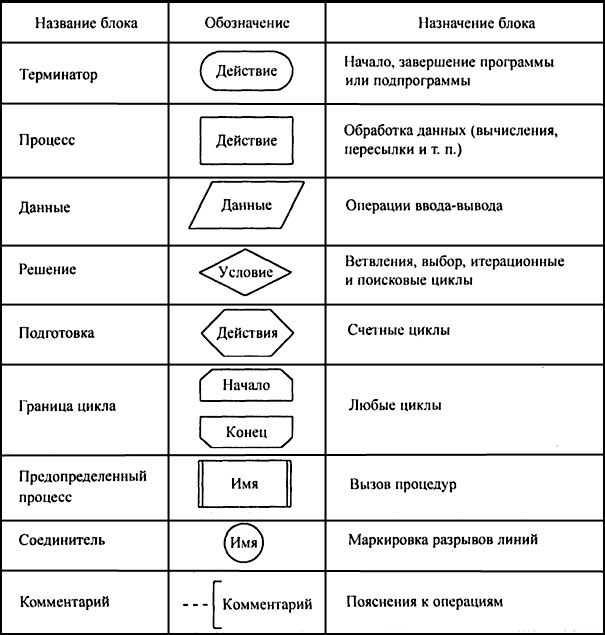
Блок-схема алгоритма – это графическое представление хода решения задачи. Блок-схема состоит из блоков, соединенных линиями, а блоки изображаются в виде геометрических фигур, называемых символами. Внутри символов записываются указания о выполняемых блоком функциях – формулы, текст, логические выражения. Вид символов и правила выполнения блок-схем стандартизированы – ГОСТ 19.701-90 содержит перечень символов, их наименования, отображаемые функции, формы и размеры, а также правила выполнения схем. При разработке алгоритма каждое действие обозначают соответствующим блоком, показывая их последовательность линиями со стрелками на конце. Названия, обозначения и назначение элементов блок-схем приводится на рис. 1.1.

Рисунок 1.1 – Основные блоки

Следует упомянуть некоторые основные правила выполнения блок-схем, которыми надлежит руководствоваться при графическом описании алгоритмов. Начало алгоритмов отмечается символом «Терминатор», из которого выходит одна линия. В нем записывается слово «Пуск» («Начало»). Конец алгоритма отмечается этим же символом, в котором записывается слово «Останов» («Конец»). В этом случае данный символ не имеет ни одной выходной линии, а на него может замыкаться одна или более линий. Символ “Процесс” может иметь одну или несколько входных линий и только одну выходную. Внутри символа может быть записано несколько предписаний – в этом случае они выполняются в порядке записи. Представление отдельных операций достаточно свободно. Для обозначения вычислений можно использовать математические выражения, для пересылки данных – стрелки, для других действий – пояснения на естественном языке, например, А: = Х + 4; i: = i + 1, < A >––> B.

Линии потока должны быть параллельны сторонам листа. Основные направления линий потока – сверху вниз и слева направо – стрелкой не обозначаются. В других случаях на конце линии потока ставится стрелка, а в месте слияния линий ставится точка. Если блок-схема не умещается на одном листе, используют соединители. При переходе на другой лист или получении управления с другого листа в комментарии указывается номер листа, например «с листа 3» «на лист 1».

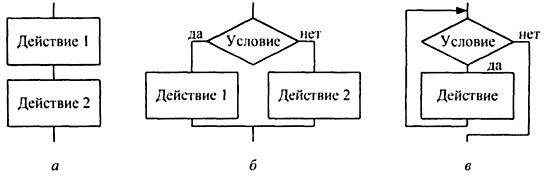
Для записи алгоритма любой сложности достаточно трех базовых структур:

1. следование — обозначает последовательное выполнение действий (рис. 1.2, а);
2. ветвление — соответствует выбору одного из двух вариантов действий (рис. 1.2, б);
3. цикл-пока — определяет повторение действий, пока не будет нарушено условие, выполнение которого проверяется в начале цикла (рис. 1.2, в).

Рисунок 1.2 – Базовые алгоритмические структуры

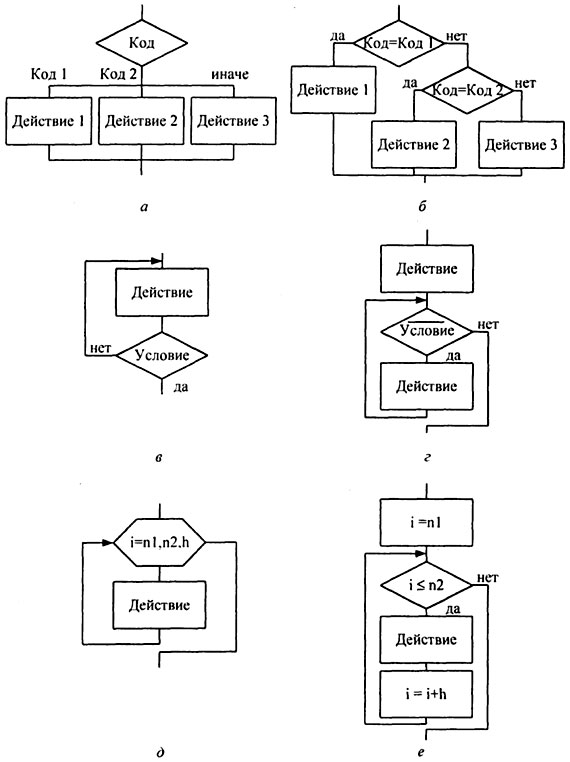
Кроме этого, при описании алгоритмов используются дополнительные алгоритмические структуры, производные от базовых, каждая из которых может быть реализована через базовые структуры:

1. выбор — выбор одного варианта из нескольких в зависимости от значения некоторой величины (рис. 1.3, а, б);
2. цикл-до — повторение некоторых действий до выполнения заданного условия, проверка которого осуществляется после выполнения действий в цикле (рис. 1.3, в, г);
3. цикл с заданным числом повторений (счетный цикл)– повторение некоторых действий указанное число раз (рис. 1.3, д, е).

Рисунок 1.3 – Реализация дополнительных алгоритмических структур

Рассмотрим примеры графического описания алгоритмов различных типов: линейного, разветвляющегося, циклического и комбинированного (рис. 1.4 – 1.7).

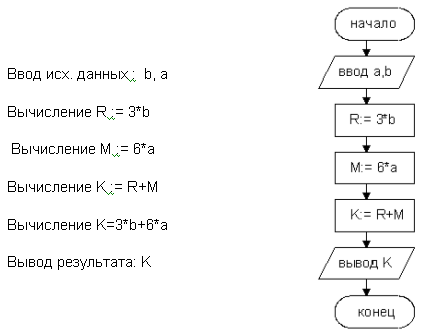
Пример 1.2. Линейный алгоритм.

Алгоритм вычисления значения выражения K=3b+6а (рис. 1.4) .

Рисунок 1.4 – Пример блок-схемы линейного алгоритма

Пример 1.3. Разветвляющийся алгоритм.

Алгоритм, определяющий, пройдет ли график функции y=3x+4 через точку с координатами x1,y1 (рис. 1.5).

Источник