Графический метод решения ЗЛП
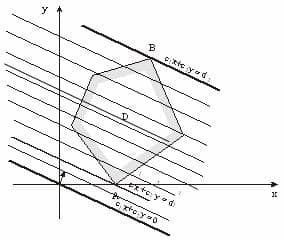
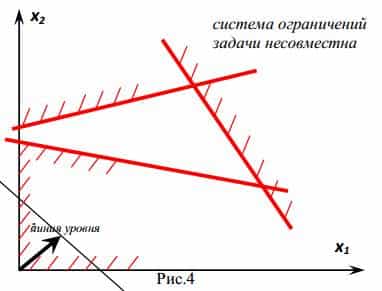
В линейном программировании используется графический метод, с помощью которого определяют выпуклые множества (многогранник решений). Если основная задача линейного программирования имеет оптимальный план, то целевая функция принимает значение в одной из вершин многогранника решений (см. рисунок).
Инструкция . Выберите количество строк (количество ограничений). Если количество переменных больше двух, необходимо систему привести к СЗЛП (см. пример и пример №2). Если ограничение двойное, например, 1 ≤ x1 ≤ 4 , то оно разбивается на два: x1 ≥ 1 , x1 ≤ 4 (т.е. количество строк увеличивается на 1).
Построить область допустимого решения (ОДР) можно также с помощью этого сервиса.
Решение матричной игры
С помощью сервиса в онлайн режиме можно определить цену матричной игры (нижнюю и верхнюю границы), проверить наличие седловой точки, найти решение смешанной стратегии методами: минимакс, симплекс-метод, графический (геометрический) метод, методом Брауна.
- На плоскости X10X2 строят прямые.
- Определяются полуплоскости.
- Определяют многоугольник решений;
- Строят вектор N(c1,c2), который указывает направление целевой функции;
- Передвигают прямую целевую функцию c1x2 + c2x2 = 0 в направлении вектора N до крайней точки многоугольника решений.
- Вычисляют координаты точки и значение целевой функции в этой точке.
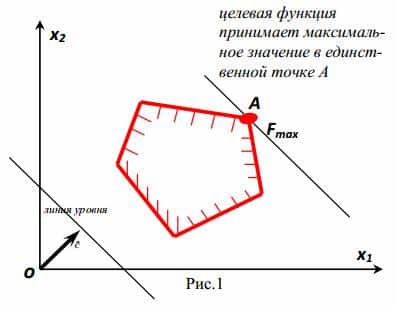
- Целевая функция принимает экстремальное (минимальное или максимальное) значение в единственной точке А.
- Сформулировать математическую модель задачи линейного программирования.
- Решить задачу линейного программирования графическим способом (для двух переменных).
Если количество переменных в задаче линейного программирования больше двух, то задачу предварительно сводят к стандартной ЗЛП.
F(X) = 3x1 — 2x2 + 5x3 — 4x5 → max при ограничениях:
x1 + x2 + x3=12
2x1 — x2 + x4=8
— 2x1 + 2x2 + x5=10
F(X) = 3x1 — 2x2 + 5x3 — 4x5
Переход к СЗЛП.
Расширенная матрица системы ограничений-равенств данной задачи:
| 1 | 1 | 1 | 0 | 0 | 12 |
| 2 | -1 | 0 | 1 | 0 | 8 |
| -2 | 2 | 0 | 0 | 1 | 10 |
Приведем систему к единичной матрице методом жордановских преобразований.
1. В качестве базовой переменной можно выбрать x3.
2. В качестве базовой переменной можно выбрать x4.
3. В качестве базовой переменной можно выбрать x5.
Поскольку в системе имеется единичная матрица, то в качестве базисных переменных принимаем X = (3,4,5).
Соответствующие уравнения имеют вид:
x1 + x2 + x3 = 12
2x1 — x2 + x4 = 8
— 2x1 + 2x2 + x5 = 10
Выразим базисные переменные через остальные:
x3 = — x1 — x2+12
x4 = — 2x1 + x2+8
x5 = 2x1 — 2x2+10
Подставим их в целевую функцию:
F(X) = 3x1 — 2x2 + 5(- x1 — x2+12) — 4(2x1 — 2x2+10)
или
F(X) = — 10x1 + x2+20 → max
Система неравенств:
— x1 — x2+12 ≥ 0
— 2x1 + x2+8 ≥ 0
2x1 — 2x2+10 ≥ 0
Приводим систему неравенств к следующему виду:
x1 + x2 ≤ 12
2x1 — x2 ≤ 8
— 2x1 + 2x2 ≤ 10
F(X) = — 10x1 + x2+20 → max
Особенности решения задач линейного программирования графическим методом
Переменную x2 принимаем в качестве дополнительной переменной и делаем замену на знак «≥»:
f=x1 + 6x3+ 27
x1 + 3x3≥6
Далее задача решается графическом способом.
Пример №2
F(X) = 3x1 — 2x2 + 5x3 — 4x5 → max при ограничениях:
x1 + x2 + x3=12
2x1 — x2 + x4=8
— 2x1 + 2x2 + x5=10
F(X) = 3x1 — 2x2 + 5x3 — 4x5
Переход к СЗЛП.
Расширенная матрица системы ограничений-равенств данной задачи:
| 1 | 1 | 1 | 0 | 0 | 12 |
| 2 | -1 | 0 | 1 | 0 | 8 |
| -2 | 2 | 0 | 0 | 1 | 10 |
Приведем систему к единичной матрице методом жордановских преобразований.
1. В качестве базовой переменной можно выбрать x3.
2. В качестве базовой переменной можно выбрать x4.
3. В качестве базовой переменной можно выбрать x5.
Поскольку в системе имеется единичная матрица, то в качестве базисных переменных принимаем X = (3,4,5).
Соответствующие уравнения имеют вид:
x1 + x2 + x3 = 12
2x1 — x2 + x4 = 8
— 2x1 + 2x2 + x5 = 10
Выразим базисные переменные через остальные:
x3 = — x1 — x2+12
x4 = — 2x1 + x2+8
x5 = 2x1 — 2x2+10
Подставим их в целевую функцию:
F(X) = 3x1 — 2x2 + 5(- x1 — x2+12) — 4(2x1 — 2x2+10)
или
F(X) = — 10x1 + x2+20 → max
Система неравенств:
— x1 — x2+12 ≥ 0
— 2x1 + x2+8 ≥ 0
2x1 — 2x2+10 ≥ 0
Приводим систему неравенств к следующему виду:
x1 + x2 ≤ 12
2x1 — x2 ≤ 8
— 2x1 + 2x2 ≤ 10
F(X) = — 10x1 + x2+20 → max
- Составить систему математических зависимостей (неравенств) и целевую функцию.
- Изобразить геометрическую интерпретацию задачи.
- Найти оптимальное решение.
- Провести аналитическую проверку.
- Определить существенные и несущественные ресурсы и их избытки.
- Определить значение целевой функции.
- Вычислить объективно обусловленные оценки.
- Составить соотношение устойчивости.
Графический метод решения задач линейного программирования с помощью таблиц Excel
Решение с помощью таблиц Excel
Вначале построим на листе Excel решение системы неравенств.
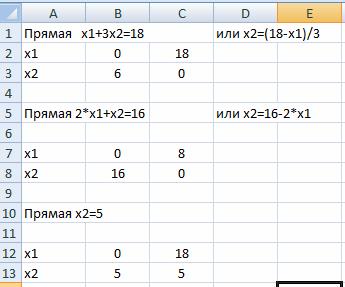
Рассмотрим первое неравенство x1+3x2≤18.
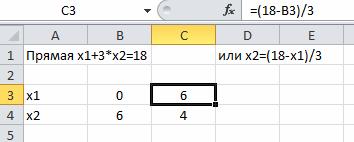
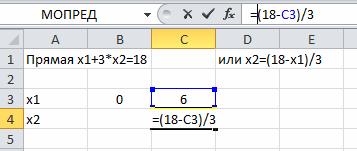
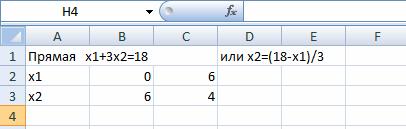
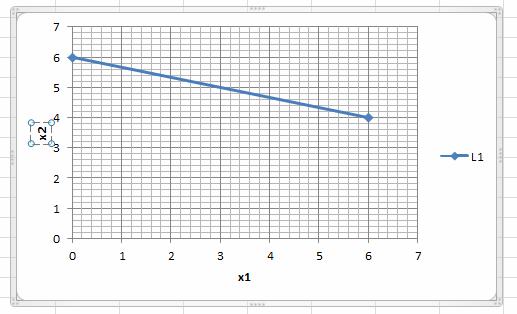
Построим граничную прямую x1+3x2=18 по двум точкам. Прямую обозначим (L1)(или Ряд1). Координаты х2 считаем по формулам:
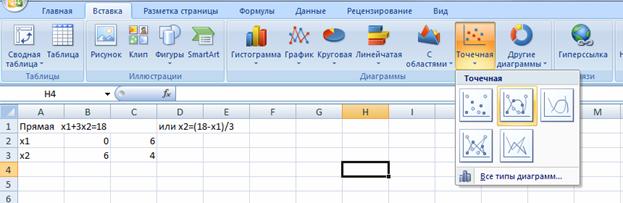
Для построения выбираем точечную диаграмму
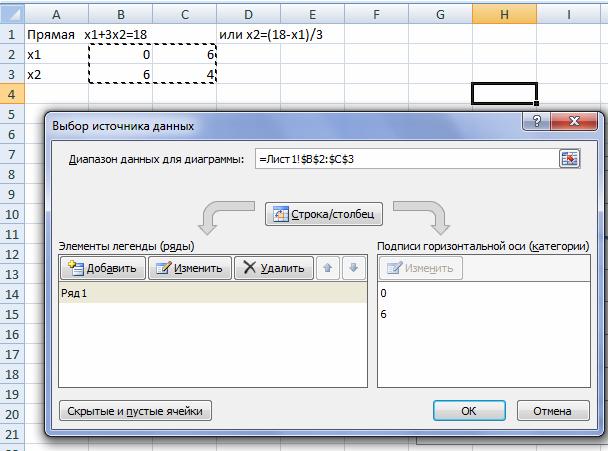
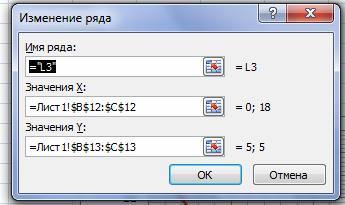
Выбираем данные для прямой
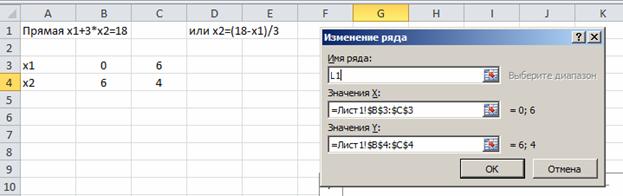
Изменяем название прямой:
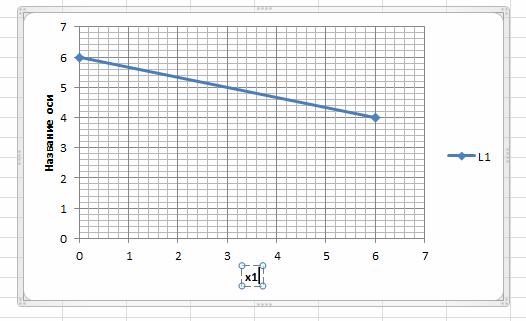
Выбираем макет диаграммы. Изменяем название осей координат:
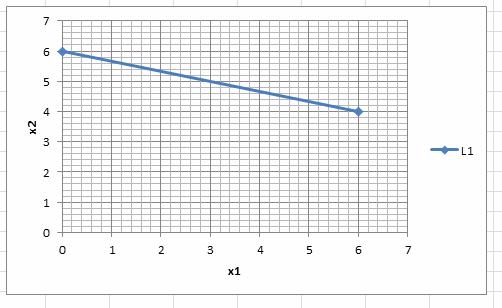
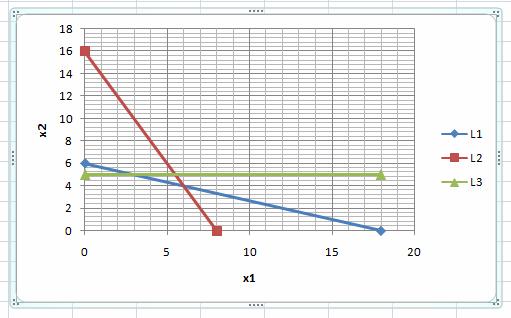
Прямая (L1) на графике:
Решение строгого неравенства x1+3x2≤18 можно найти с помощью единственной пробной точки, не принадлежащей прямой (L1). Например, с помощью точки (0; 0)Ï(L1).
При подстановке координат точки (0; 0), получаем неравенство
0 + 3×0 < 18 или 0 < 18 .
Неравенство является верным, следовательно решением неравенства (1) будет та полуплоскость, в которой пробная точка расположена (на рисунке ниже прямой L1).
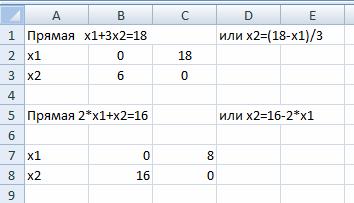
Затем решаем неравенство (2) 2x1+x2≤16.
Построим граничную прямую 2x1+x2=16 по двум точкам. Прямую обозначим (L2).
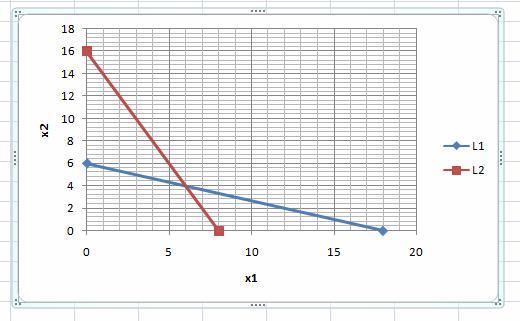
Прямая (L2) на графике:
Решение строгого неравенства 2x1+x2≤16 можно найти с помощью единственной пробной точки, не принадлежащей прямой (L2). Например, с помощью точки (0; 0)Ï(L2).
При подстановке координат точки (0; 0), получаем неравенство
2×0 + 0 < 16 или 0 < 16 .
Неравенство является верным, следовательно решением неравенства (2) будет та полуплоскость, в которой пробная точка расположена (на рисунке ниже прямой L2).
Затем решаем неравенство (3) x2≤5.
Построим граничную прямую x2=5 по двум точкам. Прямую обозначим (L3).
На листе Excel добавляем данные
Прямая (L3) на графике:
Решение строгого неравенства 2x2При подстановке координат точки (0; 0), получаем неравенство
0 < 5 .
Неравенство является верным, следовательно решением неравенства (3) будет та полуплоскость, в которой пробная точка расположена (на рисунке ниже прямой L3).
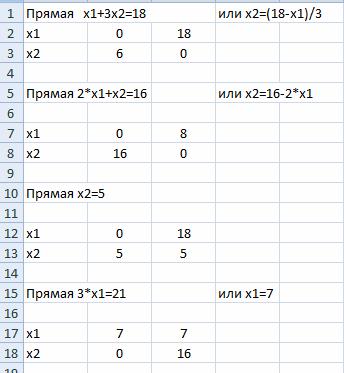
Затем решаем неравенство (4) 3x2≤21.
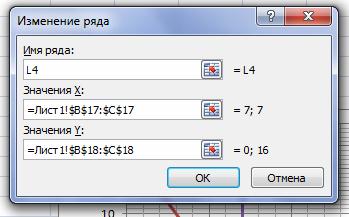
Построим граничную прямую 3x2=21 по двум точкам. Прямую обозначим (L4).
На листе Excel добавляем данные
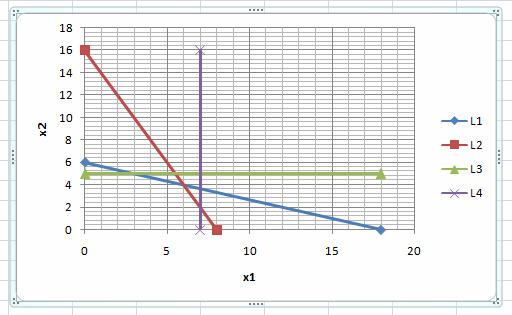
Прямая (L4) на графике:
Решение строгого неравенства 3х1 < 21 можно найти с помощью единственной пробной точки, не принадлежащей прямой (L4). Например, с помощью точки (0; 0)Ï(L4).
При подстановке координат точки (0; 0), получаем неравенство
0 < 21 .
Неравенство является верным, следовательно, решением неравенства (4) будет та полуплоскость, в которой пробная точка расположена (на рисунке левее прямой L4).
Решением двух неравенств (5) и (6) x1≥0 и x2≥0 является 1-ая четверть, ограниченная координатными прямыми x1=0 и x2=0.
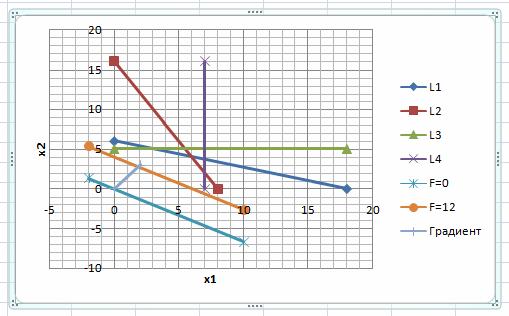
Система неравенств решена. Решением системы неравенств (1) – (6) в данном примере является выпуклый многоугольник в левом нижнем углу рисунка, ограниченный прямыми L1, L2, L3, L4 и координатными прямыми x1=0 и x2=0. Убедиться, что многоугольник выбран правильно, можно подстановкой пробной точки, например (1; 1) в каждое неравенство исходной системы. При подстановке точки (1; 1) получаем, что все неравенства, в том числе естественные ограничения, верные.
Рассмотрим теперь целевую функцию
F = 2x1 + 3x2.
Построим линии уровня для значений функции F = 0 и F = 12 (числовые значения выбраны произвольно). На листе Excel добавляем данные
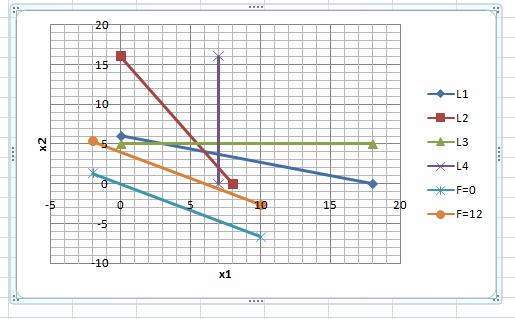
Линии уровней на графике:
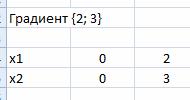
Построим вектор направлений (или градиент) . Координаты вектора совпадают с коэффициентами целевой функции F.
Добавляем на листе Excel координаты начальной и конечной точки вектора.
Вектор на рисунке:
Градиент указывает направление увеличения целевой функции F.
Теперь следует линию уровня F=0 передвинуть параллельно до последней точки угловой точки выпуклого многоугольника. Последней угловой точкой пересечения выпуклого многоугольника и передвинутой линии уровня будет точка пересечения прямых L1 и L2. Для нахождения координат точки решим систему уравнений
x1+3x2=18
2x1+x2=16
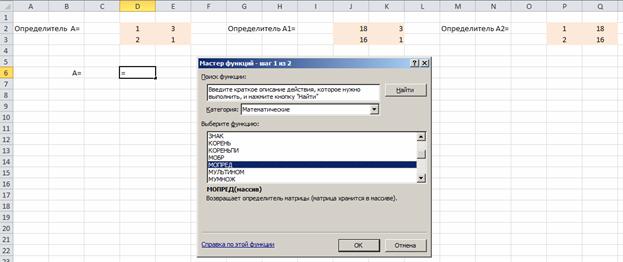
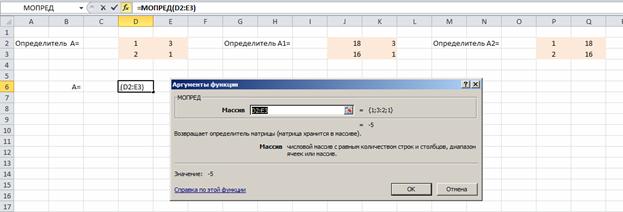
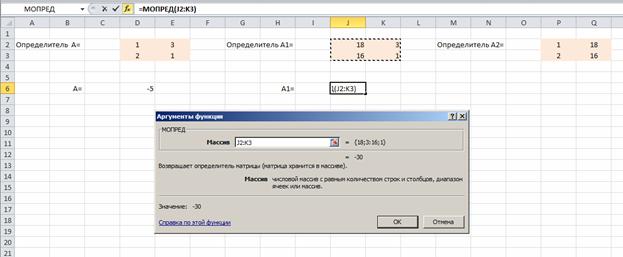
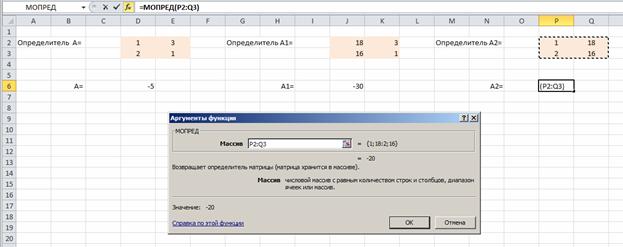
Решаем систему уравнений по формулам Крамера. Для этого на листе Excel создаем массивы для определителей. Для вычисления определителей используем математическую функцию МОПРЕД
Выделяем массив определителя
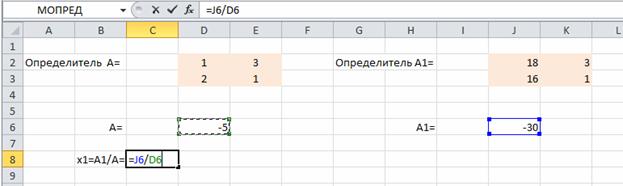
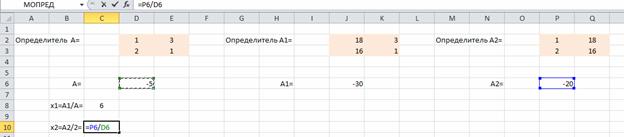
Находим значения х1 и х2
Пересечением прямых L1 и L2 будет точка с координатами (6; 4).
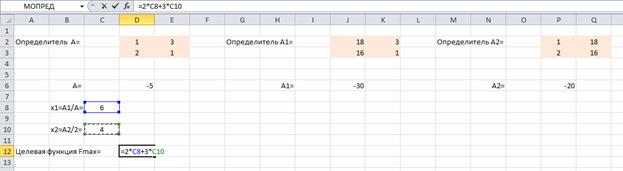
Подставляем координаты точки в целевую функцию
Fmax= 2×6 +3×4 = 24
Ответ: Fmax= 24 при x1=6 и x2=4.
Решение задач линейного программирования
графическим методом
Существуют два наиболее распространенных способа решения задач линейного программирования (ЗЛП): графический метод и симплекс-метод. Графический метод существенно нагляднее и обычно проще для понимания и решения (хотя занимает много времени, так как требует тщательного построения чертежа). Также этот метод позволяет практически одновременно найти решение на минимум и максимум, тогда как симплекс-методом придется делать «два подхода».
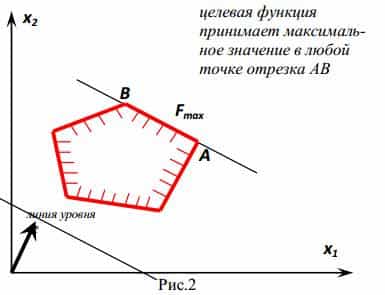
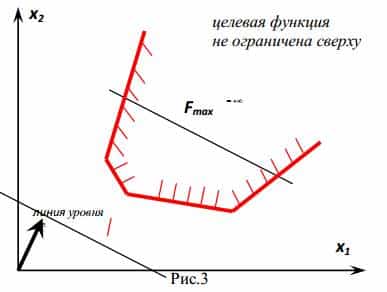
Основные шаги по решению ЗПЛ графическим методом следующие: построить область допустимых решений задачи (выпуклый многоугольник), который определяется как пересечение полуплоскостей, соответствующих неравенствам задачи, построить линию уровня целевой функции, и, наконец, двигать линию уровня в нужном направлении, пока не достигнем крайней точки области — оптимальной точки (или множества). При этом можно найти единственное оптимальное решение (точку), множество (отрезок) или ни одного (область пустая или не ограниченная в нужном направлении).
А за конкретикой — к примерам ниже: вы найдете там решенные графическим способом задачи линейного программирования. Примеры решений выложены бесплатно для вашего удобства — изучайте, ищите похожие, решайте. Если вам нужна помощь в выполнении заданий по методам оптимальных решений, перейдите в раздел: Решение задач ЛП на заказ (решаем для студентов очников и заочников).
Графический метод решения ЗЛП: примеры онлайн
Задача 1. Колхоз имеет возможность приобрести не более 19 трехтонных автомашин и не более 17 пятитонных. Отпускная цена трехтонного грузовика — 4000 руб., пятитонного — 5000 руб. Колхоз может выделить для приобретения автомашин 141 тысяч рублей. Сколько нужно приобрести автомашин, чтобы их суммарная грузоподъемность была максимальной?
Задачу решить графическими и аналитическими методами.
Задача 2. Решить задачу графическим методом на минимум и на максимум
Задача 3. Решить задачу графическим методом на минимум и на максимум
Задача 4. Среди чисел x и y, удовлетворяющих условиям
найти такие, при которых разность этих чисел y-x принимает наибольшее значение.
Задача 5. Решить графическим методом ЗЛП, заданную указанной математической моделью.
Задача 6. Решите графически следующие задачи линейного программирования
Задача 7. Решить графическим методом