Решение второй задачи егэ информатика через питон

ЗаPython’ил ЕГЭ на сотку или почему Python поможет на ЕГЭ

Доброго времени суток каждому жителю Хабрвилля! Давненько я не писал статей! Пора это исправить!

В сегодняшней статье поговорим о насущной для многих выпускников школ теме — ЕГЭ. Да-да-да! Я знаю, что Хабр — это сообщество разработчиков, а не начинающих айтишников, но сейчас ребятам как никогда нужна поддержка именно сообщества. Ребят опять посадили на дистант. Пока не ясно на какой период, но уже сейчас можно сказать, что ЕГЭ по информатике будет на компьютерах и его можно зарешать при помощи языка Python.

Вот я и подумал, чтобы не получилось как в песне, стоит этим заняться. Я расскажу про все задачи первой части и их решения на примере демо варианта ЕГЭ за октябрь.

Всех желающих — приглашаю ниже!

Быстрый перевод из системы в систему

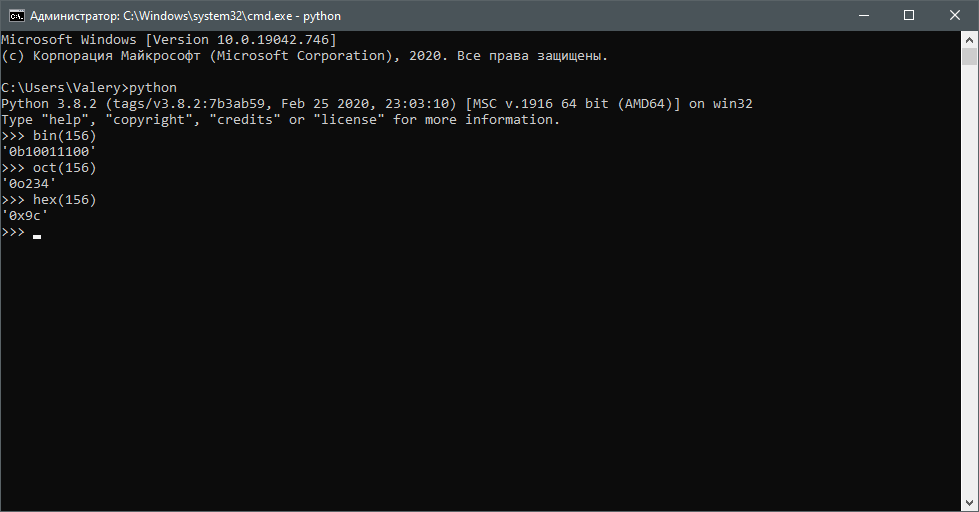
В Python есть интересные функции bin() , oct() и hex() . Работают данные функции очень просто:

bin(156) #Выводит '0b10011100' oct(156) #Выводит '0o234' hex(156) #Выводит '0x9c'

Как вы видите, выводится строка, где 0b — означает, что число далее в двоичной системе счисления, 0o — в восьмеричной, а 0x — в шестнадцатеричной. Но это стандартные системы, а есть и необычные.

Давайте посмотрим и на них:

n = int(input()) #Вводим целое число b = '' #Формируем пустую строку while n > 0: #Пока число не ноль b = str(n % 2) + b #Остатот от деления нужной системы (в нашем сл записываем слева n = n // 2 #Целочисленное деление print(b) #Вывод

Данная программа будет работать при переводе из десятичной системы счисления в любую до 9, так как у нас нет букв. Давайте добавим буквы:

n = int(input()) #Вводим целое число b = '' #Формируем пустую строку while n > 0: #Пока число не ноль if (n % 21) > 9: #Если остаток от деления больше 9. if n % 21 == 10: #. и равен 10. b = 'A' + b #. запишем слева A elif n % 21 == 11:#. и равен 11. b = 'B' + b#. запишем слева B ''' И так далее, пока не дойдём до системы счисления -1 (я переводил в 21-ную систему и шёл до 20) ''' elif n % 21 == 11: b = 'B' + b elif n % 21 == 12: b = 'C' + b elif n % 21 == 13: b = 'D' + b elif n % 21 == 14: b = 'E' + b elif n % 21 == 15: b = 'F' + b elif n % 21 == 16: b = 'G' + b elif n % 21 == 17: b = 'H' + b elif n % 21 == 18: b = 'I' + b elif n % 21 == 19: b = 'J' + b elif n % 21 == 20: b = 'K' + b else: #Иначе (остаток меньше 10) b = str(n % 21) + b #Остатот от деления записываем слева n = n // 21 #Целочисленное деление print(b) #Вывод

Способ объёмен, но понятен. Теперь давайте используем тот же функцию перевода из любой системы счисления в любую:

def convert_base(num, to_base=10, from_base=10): # Перевод в десятичную систему if isinstance(num, str): # Если число - строка, то . n = int(num, from_base) # . переводим его в нужную систему счисления else: # Если же ввели число, то . n = int(num) # . просто воспринять его как число # Перевод десятичной в 'to_base' систему alphabet = "0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ" # Берём алфавит if n < to_base: # Если число меньше системы счисления в которую переводить. return alphabet[n] # . вернуть значения номера в алфавите (остаток от деления) else: # Иначе. return convert_base(n // to_base, to_base) + alphabet[n % to_base] # . рекурсивно обратиться к функии нахождения остатка

Вызвав функцию вывода print(convert_base(156, 16, 10)) мы переведём 156 из 10 в 16 систему счисления, а введя print(convert_base('23', 21, 4)) переведёт 23 из 4-ичной в 21-ичную систему (ответ: B).

Задача 2

Все задания беру из первого октябрьского варианта (он же вариант № 9325894) с сайта Решу.ЕГЭ.

Решение данной задачи совсем простое: банальный перебор.

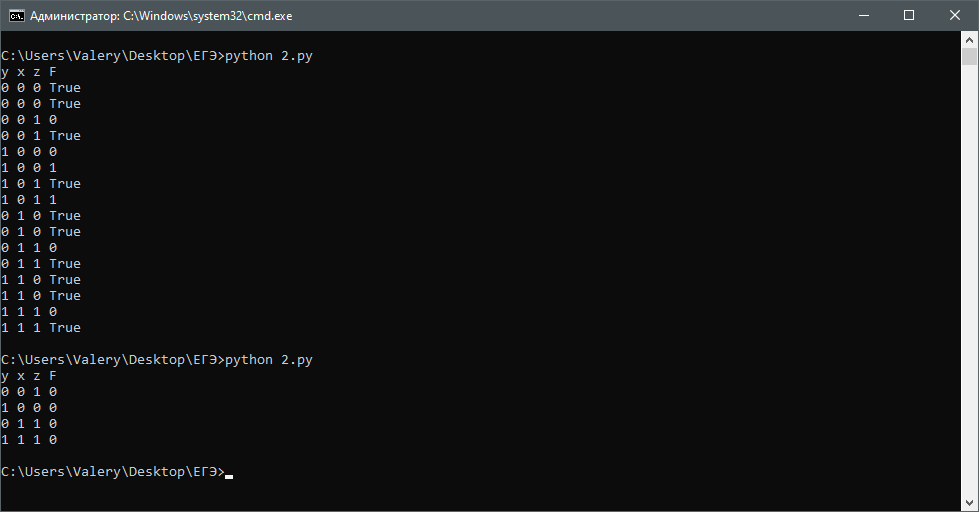
print('y', 'x', 'z', 'F') #Напечатаем заголовки таблицы for y in range(2): #Берём все переменные и меняем их в циклах '0' и '1' for x in range(2): for z in range(2): for w in range(2): F = ((not x or y) == (not z or w)) or (x and w) #Записываем функцию print(x, y, z, F) #Выводим результат

Нам вывелась вся таблица истинности (1 = True, 0 = False). Но это не очень удобно. Обратите внимание, что в задании, функция равно 0, так и давайте подправим код:

print('y', 'x', 'z', 'F') #Напечатаем заголовки таблицы for y in range(2): #Берём все переменные и меняем их в циклах '0' и '1' for x in range(2): for z in range(2): for w in range(2): F = ((not x or y) == (not z or w)) or (x and w) #Записываем функцию if not F: print(x, y, z, F) #Выводим результат

Задача 5

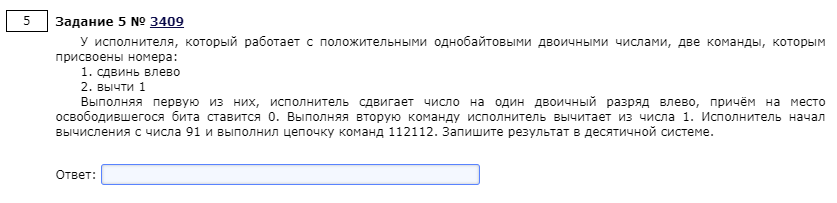
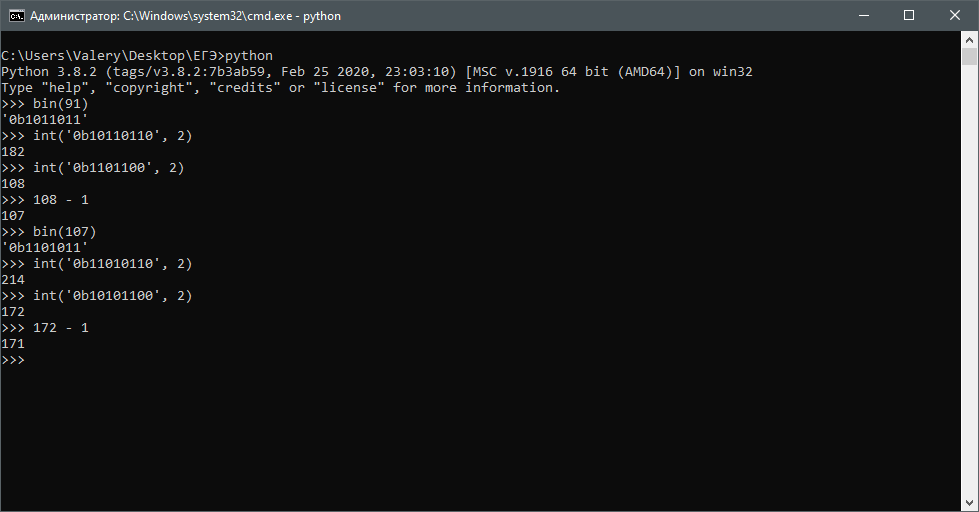
Данная задача легко решается простой последовательностью действий в интерпретационном режиме:

Задача 6

Перепечатали и получили ответ:

Задача 12

В очередной раз, просто заменим слова на код:

a = '9' * 1000 while '999' in a or '888' in a: if '888' in a: a = a.replace('888', '9', 1) else: a = a.replace('999', '8', 1) print(a)

Задача 14

Компьютер железный, он всё посчитает:

a = 4 ** 2020 + 2 ** 2017 - 15 k = 0 while a > 0: if a % 2 == 1: k += 1 a = a // 2 print(k)

Задача 16

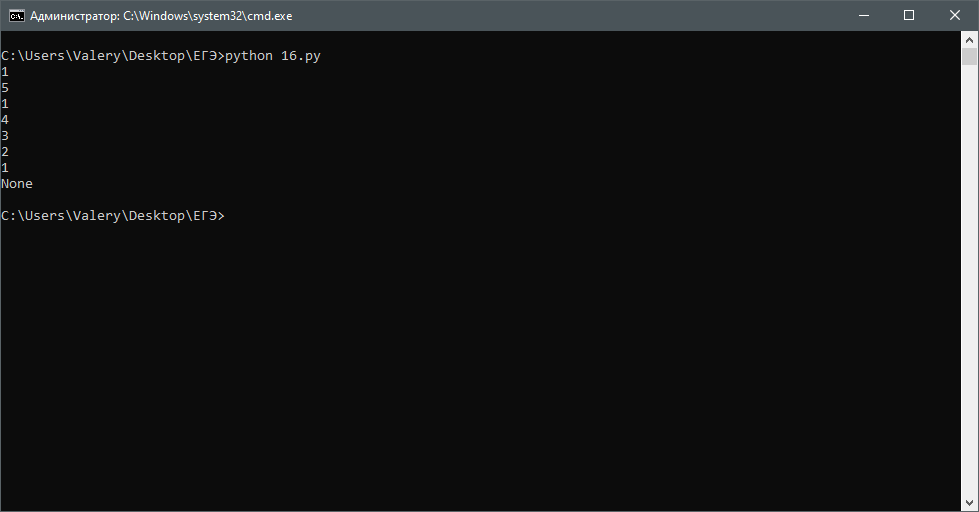
Опять же, просто дублируем программу в python:

def F(n): if n > 0: F(n // 4) print(n) F (n - 1) print(F(5))

Задача 17

Задача с файлом. Самое сложное - достать данные из файла. Но где наша не пропадала?!

with open("17.txt", "r") as f: #Открыли файл 17.txt для чтения text = f.read() #В переменную text запихнули строку целиком a = text.split("\n") #Разбили строку энтерами (\n - знак перехода на новую строку) k = 0 #Стандартно обнуляем количество m = -20001 #Так как у нас сумма 2-ух чисел и минимальное равно -10000, то минимум по условию равен -20000, поэтому. for i in range(len(a)): #Обходим все элементы массива if (int(a[i - 1]) % 3 == 0) or (int(a[i]) % 3 == 0): #Условное условие k += 1 #Счётчик if int(a[i - 1]) + int(a[i]) > m: #Нахождение минимума m = int(a[i - 1]) + int(a[i]) print(k, m) #Вывод

Немного пояснений. Функция with() открывает файл считывает данные при помощи функции read() и закрывает файл. В остальном - задача стандартна.

Задача 19, 20 и 21

Все три задачи - задачи на рекурсию. Задачи идентичны, а вопросы разные. Итак, первая задача:

Пишем рекурсивную функцию и цикл перебора S:

def f(x, y, p): #Рекурсивная функция if x + y >= 69 or p > 3: #Условия завершения игры return p == 3 return f(x + 1, y, p + 1) or f(x, y + 1, p + 1) or\ f(x * 2, y, p + 1) or f(x, y * 3, p + 1) #Варианты действий for s in range (1, 58 + 1): #Перебор S if f(10, s, 1): #Начали с 10 камней print(s) break

Немного пояснений. В рекурсивной функции существует 3 переменные x - число камней в первой куче, y - число камней во второй куче, p - позиция. Позиция рассчитывается по таблице:

Источник

Решение второй задачи егэ информатика через питон

Конъю́нкция (от лат. conjunctio — «союз, связь») — логическая операция, по смыслу максимально приближенная к союзу «и»
Наиболее часто в заданиях будет отображаться как " /\ ", реже как " & ".
В питоне мы будем заменять на " and ".

Дизъю́нкция (от лат. disjunctio — «разобщение»), логи́ческое сложе́ние, логи́ческое ИЛИ, включа́ющее ИЛИ; иногда просто ИЛИ — логическая операция, по своему применению максимально приближённая к союзу «или» в смысле «или то, или это, или оба сразу».
Наиболее часто в заданиях будет отображаться как " /\ ", реже как " & ".
В заданиях №2 отображается как " \/ ", иногда " || ".
В питоне мы будем заменять на " or ".

Отрица́ние (инве́рсия, от лат. inversio — переворот, логи́ческое «НЕ») в логике — унарная операция над суждениями, результатом которой является суждение, «противоположное» исходному. Обозначается знаком ¬ перед или чертой — над суждением.
В питоне если перед переменной ¬ или — над суждением ставим переменную в скобки и перед ней ставим " not( ) ".

Имплика́ция (от лат. implicatio «связь; сплетение») — бинарная логическая связка, по своему применению приближенная к союзам «если…, то…».
Импликация записывается как посылка ⇒ следствие; применяются также стрелки другой формы и направленные в другую сторону, но всегда указывающие на следствие.
В коде заменяем на "

Логическая равнозначность или эквиваленция (или эквивале́нтность[1]) — это логическое выражение, которое является истинным тогда, когда оба простых логических выражения имеют одинаковую истинность. Двуместная логическая операция обычно обозначается символом ≡ или ↔.
В питоне обозначаем двумя знаками равно " == ".

Для всех заданий справедлива одна конструкция решения. Давайте её разберём на примере: Задание взято с сайта "СДАМ ГИА: РЕШУ ЕГЭ"

1. Для начала внимательно посмотрим на таблицу, всего переменных 3 - x, y и z. Также нам надо найти где функция принимает значение 0, то есть ложно.

᠌ ᠌ ᠌ ᠌ ᠌ ᠌ ᠌ ᠌1) Прописываем print("x, y, z, w") - для того, чтобы когда мы видели, какая переменная
᠌ ᠌ ᠌ ᠌ ᠌ ᠌ ᠌ ᠌ ᠌᠌ ᠌ ᠌ ᠌отвечает за какое значение.

᠌ ᠌ ᠌ ᠌ ᠌ ᠌ ᠌ ᠌2) Задаём каждой переменной значение, которое она может принимать - " 0 " или " 1 "
᠌ ᠌ ᠌ ᠌ ᠌ ᠌ ᠌ ᠌ ᠌ (пишем in range(2) потому, что учитывается интервал от 0 до 2 не включительно, то есть
᠌ ᠌ ᠌ ᠌ ᠌ ᠌ ᠌ ᠌ ᠌᠌ ᠌ ᠌᠌ ᠌можно просто написать в скобках 2, а не in range(0, 2)

᠌ ᠌ ᠌ ᠌ ᠌ ᠌ ᠌ ᠌3) Записываем условие с помощью " if ", дальше прописываем нашу функцию и значение
᠌ ᠌ ᠌ ᠌ ᠌ ᠌ ᠌ ᠌ ᠌᠌ ᠌ ᠌ ᠌которое оно принимает:
᠌ ᠌ ᠌ ᠌ ᠌ ᠌ ᠌ ᠌ ᠌᠌ ᠌ ᠌ ᠌* Если F = 0, то всё условие ставим в скобки и перед ними ставим not -> not(вся
᠌ ᠌ ᠌ ᠌ ᠌ ᠌ ᠌ ᠌ ᠌᠌ ᠌ ᠌᠌ ᠌ ᠌ ᠌функция). Также можно вставить функцию в скобки и написать после неё написать " ==
᠌ ᠌ ᠌ ᠌ ᠌ ᠌ ᠌ ᠌ ᠌᠌ ᠌ ᠌ ᠌ ᠌ ᠌False"
᠌ ᠌ ᠌ ᠌ ᠌ ᠌ ᠌ ᠌ ᠌᠌ ᠌ ᠌᠌ ᠌* Иначе F = 1, ничего не делаем с функцией; или ставим её в скобки, а в конце пишем "
᠌ ᠌ ᠌ ᠌ ᠌ ᠌ ᠌ ᠌ ᠌᠌ ᠌ ᠌ ᠌ ᠌ ᠌== True"

᠌ ᠌ ᠌ ᠌ ᠌ ᠌ ᠌ ᠌4) Пишем print(x, y, z, w) и запускаем код, выведенные значения сопоставляем с ᠌ ᠌ ᠌ ᠌ ᠌᠌ ᠌ ᠌ ᠌᠌ ᠌ ᠌ ᠌ ᠌᠌ ᠌ ᠌ ᠌ ᠌᠌ ᠌ ᠌ ᠌ ᠌᠌ ᠌ ᠌ ᠌ ᠌᠌ ᠌ ᠌ ᠌ ᠌таблицей ᠌и правильно вписываем, строки с таблице не должны повторяться!

print('x,y,z,w')
for x in range(2):
for y in range(2):
for z in range(2):
for w in range(2):
if (условие в задание) == True/False:
print(x, y, z ,w)

К сожалению, стим убирает отступы, так, что когда копировать будите - отступы делайте, чтобы код работал

Источник

Читайте также:  Can we create private class in java