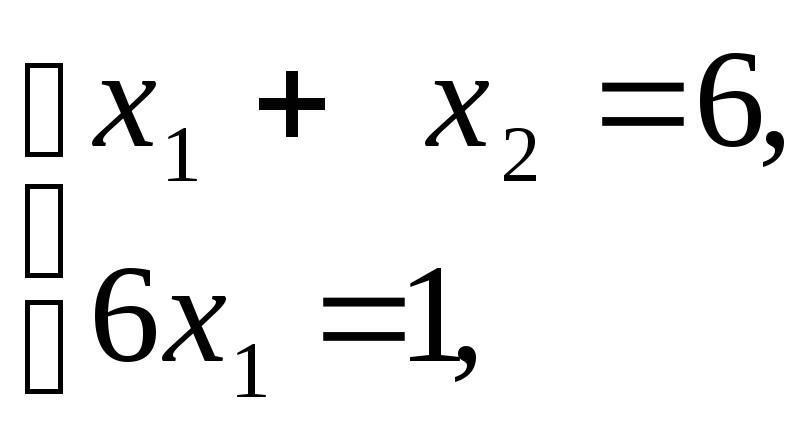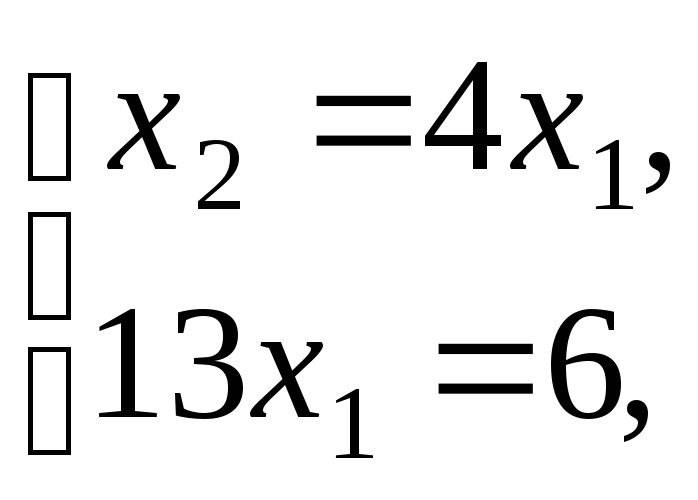1. Общая постановка задачи линейного программирования. Графическое решение злп. Каноническая форма. Базисное решение
Система неравенств (1.1.1) называется системой ограничений задачи.
Неравенства (1.1.2) – условие не отрицательности переменных. Функция (1.1.3) – функция цели (целевая функция).
Вектор , удовлетворяющий неравенствам (1.1.1) и (1.1.2), называется планом задачи линейного программирования или допустимым вектором, или допустимым решением.
Множество всех допустимых векторов x будем обозначать буквой G и называть допустимым множеством или множеством планов.
Вектор называется оптимальным решением или оптимальным планом, если для всех ( ).
Если оптимальное решение может быть найдено, то задача называется разрешимой, если же оптимального решения не существует, то задача называется неразрешимой.
Причины, по которым не может быть найдено оптимальное решение:
1. Функция на допустимом множестве G неограниченна. Эта задача называется неразрешимой из-за неограниченности целевой функции.
2. Допустимое множество G пусто ( ), то есть не существует допустимых решений.
Такая задача называется несовместимой.
. Графический метод решения задачи линейного программирования
Если задача линейного программирования имеет две переменные x1 и x2, то ее можно решить графически.
Решение задачи происходит в два этапа.
На первом этапе необходимо на плоскости изобразить допустимое множество, а на втором найти оптимальную точку, если она существует, в противном случае убедиться в неразрешимости задачи.
Этап 1. Построение допустимого множества
Каждое неравенство в рассматриваемой задаче представляет собой полуплоскость, а допустимое множество – пресечение этих полуплоскостей. Если неравенства в задаче заменить уравнениями, то получим уравнения прямой. Каждую прямую можно построить по двум точкам. Для того чтобы выделить необходимую полуплоскость, надо взять точку, не лежащую на прямой, и подставить ее координаты в левую часть неравенства. Если неравенство выполнено, то выбираем полуплоскость, содержащую данную точку, в противном случае — другую полуплоскость.
Так как в ограничениях присутствуют ограничения неотрицательности переменных, то рассматриваем только первый координатный угол.
Если правая часть не равна нулю, то в качестве пробной точки удобнее всего выбрать начало координат (0,0).
Алгоритм выполнения первого этапа
Шаг 1: Выделение первого координатного угла.
Шаг 3: i-е неравенство записывается как уравнение.
Шаг 4: Полагаем, находим из уравнения.
Шаг 5: Полагаем, находим из уравнения.
Шаг 6: Через точку и проводится прямая.
Шаг 7: В левую часть неравенства подставляется точка с координатами . Если неравенство выполнено, то выбирается полуплоскость, содержащая начало координат, в противном случае — противоположная полуплоскость.
Шаг 8: Если , то , переходим к Шагу 3, иначе Шаг 9.
Шаг 9: Допустимое множество получено. Если оно пустое ( ), то выписывается ответ: «Задача несовместна», иначе переход к Этапу 2.
Этап 2: Поиск оптимальной точки
Рассмотрим градиент функции . Так как функция линейна, то ее градиент есть постоянный вектор с координатами .
Известно, что движение в направлении градиента увеличивает значение функции.
Прямая, перпендикулярная вектору-градиенту, называется линией уровня, так как значения функции в любой точке этой прямой одинаковы.
Алгоритм выполнения второго этапа
Шаг 1: Строится вектор градиент .
Шаг 2: Кладется линейка перпендикулярно вектору–градиенту.
Шаг 3: Линейка сдвигается параллельно самой себе по направлению вектора-градиента, пока хотя бы одна точка соответствующей прямой принадлежит допустимому множеству.
Шаг 4: Если при любом положении линейки перпендикулярно вектору-градиенту имеются точки допустимого множества, то выписывается ответ: «Задача неразрешима из-за неограниченности целевой функции» и переход к Шагу 10. Иначе Шаг 5.
Шаг 5: Находится последняя точка допустимого множества, лежащая на соответствующей линии уровня.
Шаг 6: Если эта точка неединственная, то выбирается точка, которая является пересечением двух прямых, ограничивающих допустимое множество.
Шаг 7: Выписывается система двух уравнений с двумя неизвестными.
Шаг 8: Из системы уравнений находится оптимальная точка .
Шаг 9: Находится оптимальное значение целевой функции .
Пример 1.1. Решить задачу линейного программирования графически.
Решение. Строим допустимое множество в соответствии с первым этапом алгоритма. В результате получаем ограниченную многогранную область (рис. 1.1).
В табл. 1.1 заданы точки, по которым строятся прямые (1.2.1)-(1.2.3).
2.2. Графический метод решения задачи линейного программирования
Графический метод решения ЗЛП основан на утверждениях, приведенных в пункте 2.1. Согласно теореме 2, оптимальное решение находится в вершине области допустимых решений и поэтому решить ЗЛП – найти вершину области допустимых решений, координаты которой дают оптимальное значение целевой функции.
Графический метод используют для решения ограниченного класса задач с двумя переменными, иногда с тремя переменными. Надо заметить, что для трех переменных эта область является недостаточно наглядной.
Алгоритм графического метода решения злп
- Построить прямые линии, уравнения которых получаем заменой в системе ограничений (2.1.2) знаков неравенств на знаки равенств.
- Определить полуплоскости, соответствующие каждому неравенстве задачи.
- Найти многоугольник решений ЗЛП, учитывая, что
.
- Построить вектор направлений
=(с1,с2), который указывает направление наибольшего возрастания целевой функции ЗЛП (2.1.1).
- Построить прямую z, которая проходит через область допустимых решений, перпендикулярно к вектору
:
. Это линия уровня.
- Переместить прямую
в направлении вектора
в случае максимизации целевой функции (или в противоположном направлении в случае минимизации целевой функции), найти вершину многоугольника решений ЗЛП, в которой целевая функция достигает экстремального значения.
- Определить координаты точки, в которой целевая функция достигает оптимальное значения, и вычислить экстремальное значение целевой функции в этой точке.
Реализацию графического метода решения ЗЛП рассмотрим на примерах. Пример 2.2.1. Решить ЗЛП графическим методом: 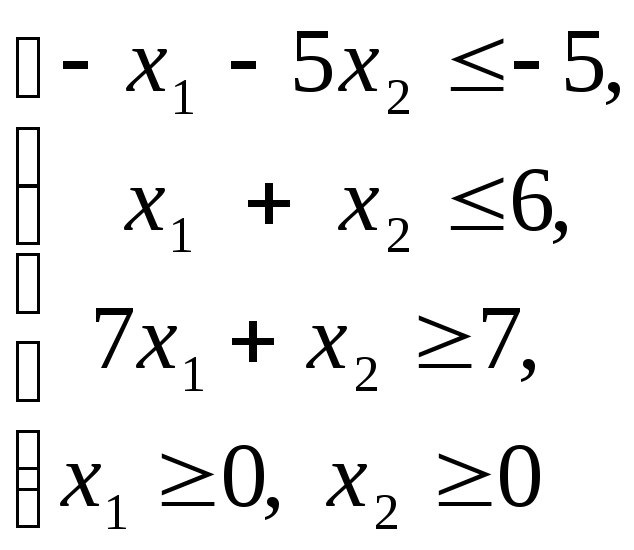
| Замечание. | Для удобства построения прямой линии, ее уравнение можно привести к виду в отрезках на осях  , (2.2.3) где параметры а,b– длины отрезков, отсекаемых прямой на соответствующих осяхОх1,Ох2 . , (2.2.3) где параметры а,b– длины отрезков, отсекаемых прямой на соответствующих осяхОх1,Ох2 . |
| Замечание. | Если уравнение прямой линии имеет вид:  , то она проходит через точку с координатами (0;0). Для ее построения следует выразитьx2 через x1, и найти еще одну точку. , то она проходит через точку с координатами (0;0). Для ее построения следует выразитьx2 через x1, и найти еще одну точку. |
Для приведения уравнения прямой l1 к виду (2.2.3.) разделим обе его части на 5: 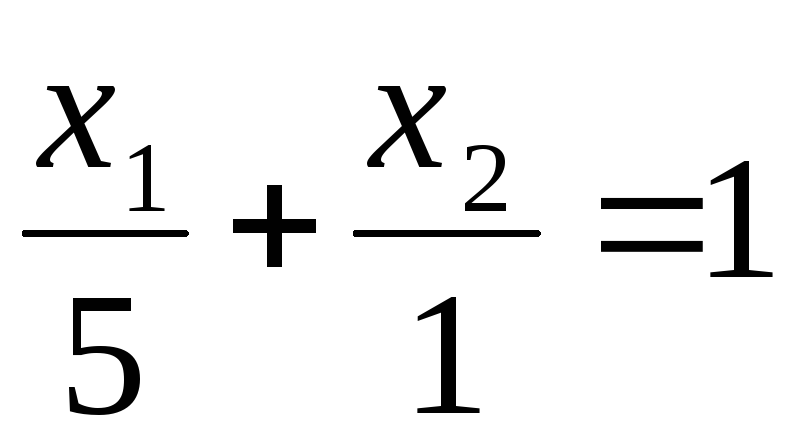
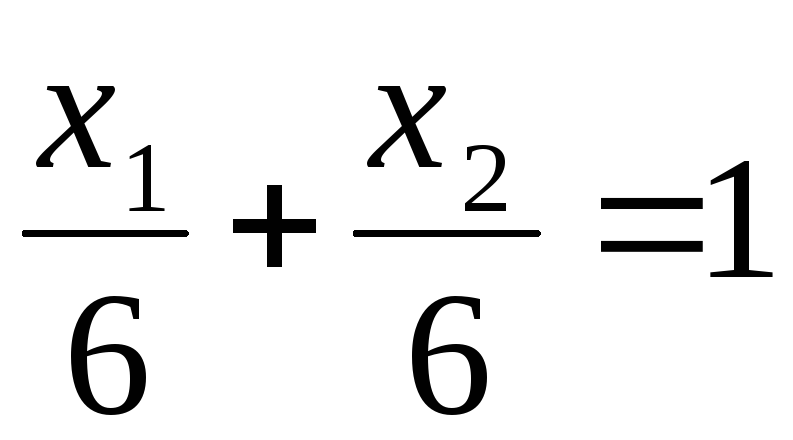
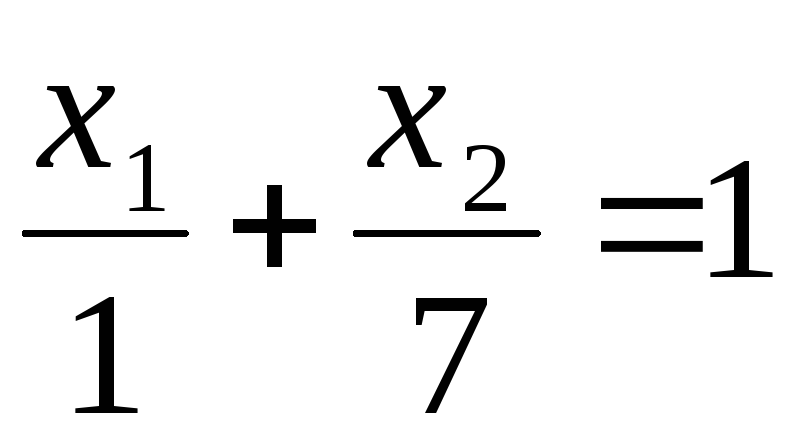
| Замечание. | В качестве точки сравнения целесообразно выбирать, если это возможно, точку О(0,0). |
Таким образом, первая и вторая искомые полуплоскости расположены в противоположную сторону от начала координат (0 – 5·0


| Замечание. | В силу ограничений х1 0,х2 0,х2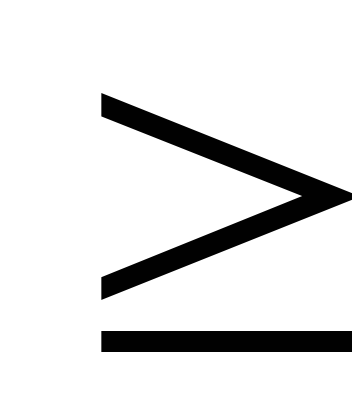 0, область допустимых решений ЗЛП всегда лежит в первой четверти координатной плоскости. 0, область допустимых решений ЗЛП всегда лежит в первой четверти координатной плоскости. |
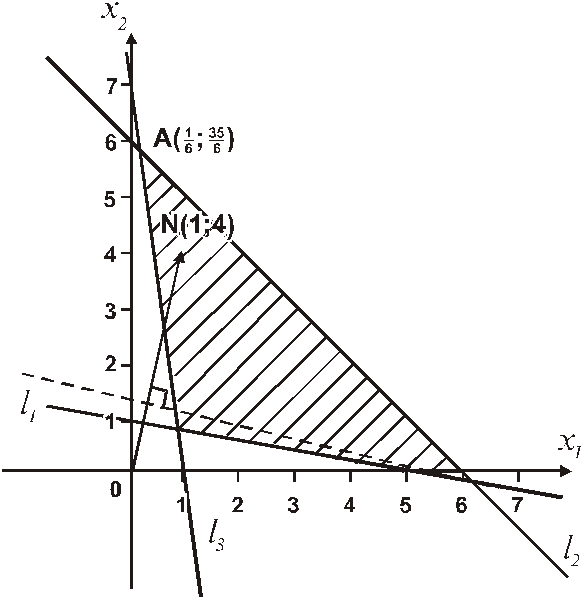



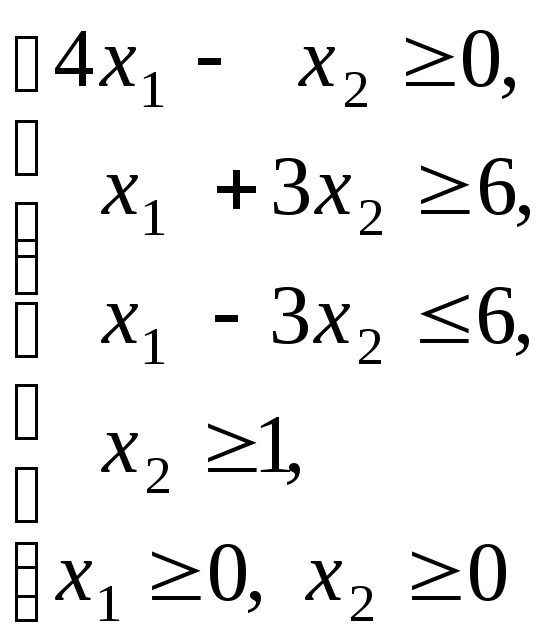
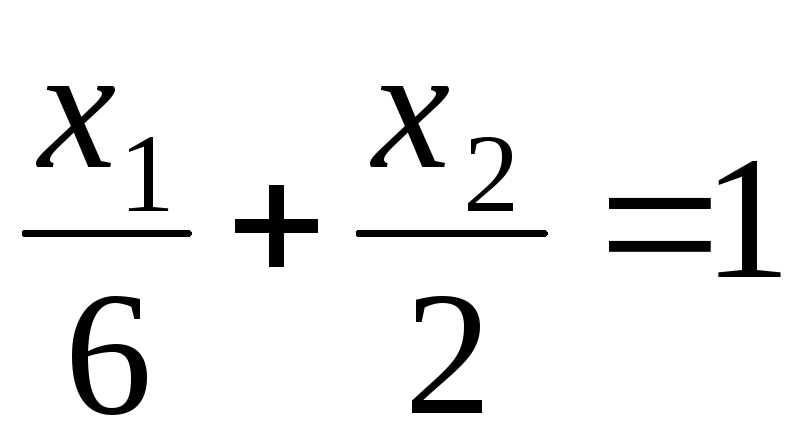
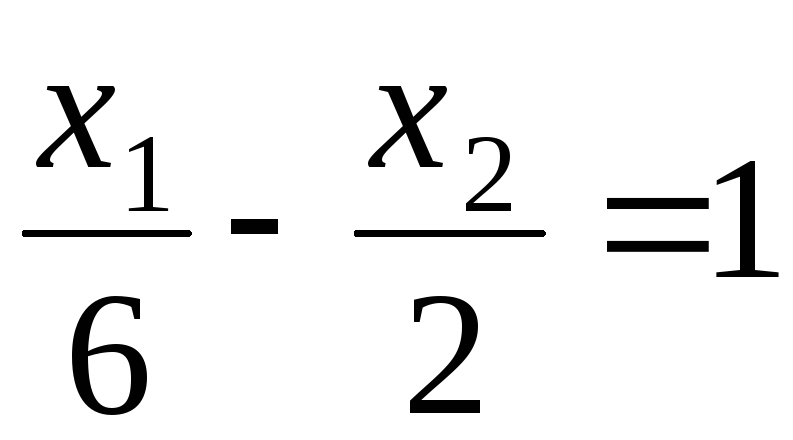

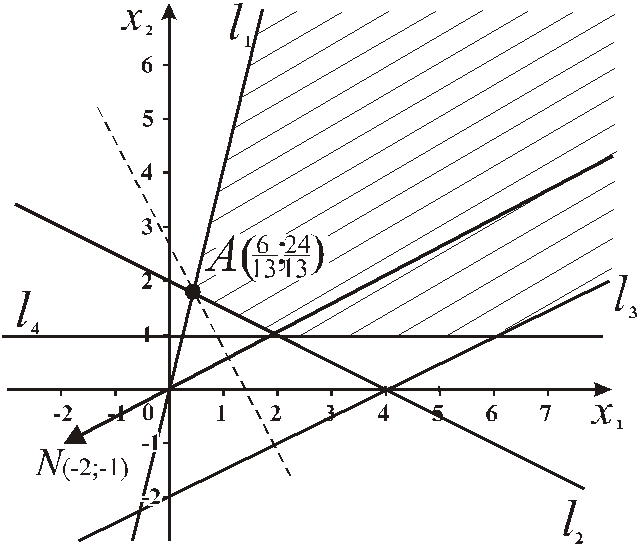

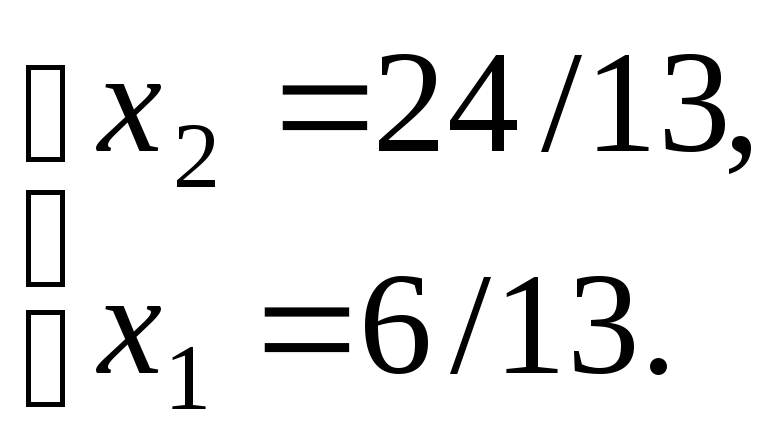
- Целевая функция достигает оптимального значения в единственной вершине многоугольника решений;
- Целевая функция достигает оптимальное значение в любой точке ребра многоугольника решений (ЗЛП имеет альтернативные опорные планы с одинаковыми значениями z);
- ЗЛП не имеет оптимальных планов;
- ЗЛП имеет оптимальный план в случае неограниченной области допустимых решений.
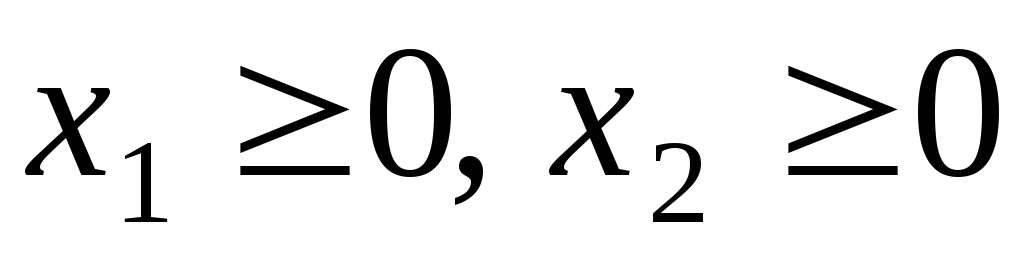 .
. =(с1,с2), который указывает направление наибольшего возрастания целевой функции ЗЛП (2.1.1).
=(с1,с2), который указывает направление наибольшего возрастания целевой функции ЗЛП (2.1.1).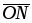 :
: . Это линия уровня.
. Это линия уровня.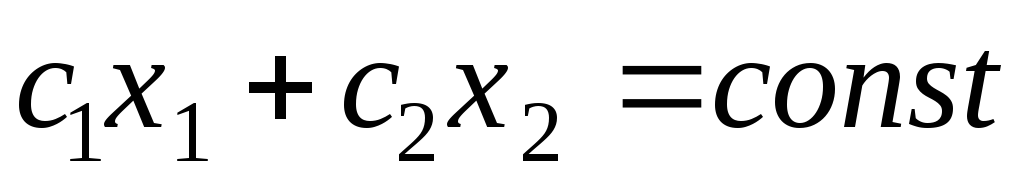 в направлении вектора
в направлении вектора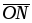 в случае максимизации целевой функции (или в противоположном направлении в случае минимизации целевой функции), найти вершину многоугольника решений ЗЛП, в которой целевая функция достигает экстремального значения.
в случае максимизации целевой функции (или в противоположном направлении в случае минимизации целевой функции), найти вершину многоугольника решений ЗЛП, в которой целевая функция достигает экстремального значения.