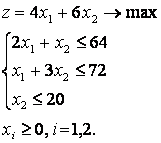Решение экономической задачи линейного программирования симплекс методом

3.2. Симплекс-метод решения задач линейного программи­рования

Поскольку, как было показано в п. 3.1 решение задачи линейного программирования находится в одной из крайних (угловых) точек ОДЗ, важным вопросом является изучение не системы неравенств (4), а соответствующей системы уравнений AX = B, решение которой дает угловые точки ОДЗ.

Если уравнения системы АX = B линейно независимы, то система имеет множество решений при n > m и единственное решение при n = m. При решении задачи линейного программирования симплекс-методом всегда будет выполняться n > m, поэтому для получения некоторого одного решения, «лишние» n – m переменных приравниваются нулю.

Если приравнять к нулю n – m произвольных переменных (например, переменные x_m+1, x_m+2, …, x_n) и, решив систему, найти значения оставшихся m переменных (x₁, x₂, …, x_m), то такое решение называется базисным.

Если нулю приравнять некоторые другие n – m переменных – получим другое базисное решение. Любое базисное решение, у которого все переменные неотрицательные называется допустимым базисным решением.

Переменные, которые были приравнены нулю, называются небазисными. Оставшиеся т переменных, значение которых получены из решения системы, называются базисными.

Допустимое базисное решение представляет собой угловую вершину ОДЗ.

Решение задачи симплекс-методом сводится к направленному перебору смежных друг с другом угловых точек, которые представляют собой допустимые базисные решения.

Сформулируем в общем виде алгоритм симплекс-метода:

1: Приведение задачи к стандартной форме. Стандартной формой задачи линейного программирования будем называть задачу, у которой все ограничения записаны как равенства и при этом правые части ограничений неотрицательны.

2: Выделение исходного базисного решения (по возможности из стандартной формы). То есть определение тех переменных n – m переменных, которые приравниваются нулю и нахождение значений оставшихся базисных переменных.

3: Определение, является ли полученное базисное решение оптимальным, если да, то решение окончено, иначе переходим к шагу 4.

4: Определение переменной, которая войдет в базис и переменной, которая из базиса выйдет таким образом, чтобы новое решение было лучше предыдущего. То есть, если текущее базисное решение неоптимально, необходимо определить, какую из базисных переменных приравнять нулю, и какую из небазисных переменных вместо нее включить в базис.

5: Использование эквивалентных преобразований методом Жордана-Гаусса для нахождения нового допустимого базисного решения. Переход к шагу 3.

Чтобы привести задачу линейного программирования к стандартной форме необходимо:

1. Убедиться, что во всех ограничениях правые части b_i неотрицательны. Если есть отрицательные правые части ограничений, такие ограничения нужно умножить на –1 (при этом учесть, что в ограничениях типа  или  знак ограничения изменится на противоположный).

2. К левой части ограничений типа  нужно прибавить новую, дополняющую переменную S, которая уравнивала бы левую и правую часть и показывала бы насколько левая часть ограничения меньше правой.

в стандартном виде будет выглядеть так:

3. Из левой части ограничений типа  нужно вычесть новую, избыточную переменную e, которая уравнивала бы левую и правую часть и показывала бы насколько левая часть ограничения больше правой.

в стандартном виде будет выглядеть так:

Дополняющие переменные S и избыточные e будем называть вспомогательными, в то время, как переменные x – основными.

Чтобы из стандартной формы сразу выделить базисное решение, необходимо в качестве базисных переменных выбрать те m переменных, каждая из которых встречается только в одном из уравнений и включена в него с коэффициентом, равным единице.

В качестве исходных базисных переменных в задачах с ограничениями  удобно брать переменные S₁, …, S_n.

Реализацию алгоритма симплекс-метода проиллюстрируем на следующем примере.

Пример 3.2. Мебельная фабрика может производить шкафы, столы, стулья. При изготовлении мебели используются древесина, труд рабочих на столярном и отделочном участках. Необходимое количество ресурсов для изготовления шкафов, столов и стульев приведено в таблице:

Таблица 3.1 – Исходные данные к примеру 3.2

Источник

Решение задач линейного программирования
симплексным методом

Если вы уже разобрались с графическим методом решения задач линейного программирования, самое время переходить к симплекс-методу. В отличие от первого, он практически не имеет ограничений на задачу (любое количество переменных, разные знаки и т.п.) и модифицируется в зависимости от типа задачи (например, М-метод или метод искусственного базиса).

При решении задачи симплекс методом вычисления обычно ведутся (для компактности и наглядности) в таблицах (табличный симплекс-метод), причем последняя таблица с оптимальным решением содержит важную дополнительную информацию: решение двойственной задачи, остатки ресурсов, сведения о дефицитных ресурсах и т.п., которая позволяет провести экономический анализ задачи линейного программирования (см. ниже пример 3).

Примеры решений задач симплекс-методом выложены бесплатно для вашего удобства — изучайте, ищите похожие, решайте. Если вам нужна помощь в выполнении подобных заданий, перейдите в раздел: решение линейного программирования на заказ.

Решение задач симплекс-методом: примеры онлайн

Задача 1. Компания производит полки для ванных комнат двух размеров — А и В. Агенты по продаже считают, что в неделю на рынке может быть реализовано до 550 полок. Для каждой полки типа А требуется 2 м2 материала, а для полки типа В — 3 м2 материала. Компания может получить до 1200 м2 материала в неделю. Для изготовления одной полки типа А требуется 12 мин машинного времени, а для изготовления одной полки типа В — 30 мин; машину можно использовать 160 час в неделю. Если прибыль от продажи полок типа А составляет 3 денежных единицы, а от полок типа В — 4 ден. ед., то сколько полок каждого типа следует выпускать в неделю?

Задача 2. Решить задачу линейного программирования симплекс-методом.

Задача 3. Предприятие производит 3 вида продукции: А1, А2, А3, используя сырьё двух типов. Известны затраты сырья каждого типа на единицу продукции, запасы сырья на планируемый период, а также прибыль от единицы продукции каждого вида.

1. Сколько изделий каждого вида необходимо произвести, чтобы получить максимум прибыли?
2. Определить статус каждого вида сырья и его удельную ценность.
3. Определить максимальный интервал изменения запасов каждого вида сырья, в пределах которого структура оптимального плана, т.е. номенклатура выпуска, не изменится.
4. Определить количество выпускаемой продукции и прибыль от выпуска при увеличении запаса одного из дефицитных видов сырья до максимально возможной (в пределах данной номенклатуры выпуска) величины.
5. Определить интервалы изменения прибыли от единицы продукции каждого вида, при которых полученный оптимальный план не изменится.

Задача 6. Решить задачу симплекс-методом, рассматривая в качестве начального опорного плана, план, приведенный в условии:

Задача 7. Решить задачу модифицированным симплекс-методом.
Для производства двух видов изделий А и Б используется три типа технологического оборудования. На производство единицы изделия А оборудование первого типа используется а1=4 часов, оборудование второго типа а2=8 часов, а оборудование третьего типа а3=9 часов. На производство единицы изделия Б оборудование первого типа используется б1=7 часов, оборудование второго типа б2=3 часов, а оборудование третьего типа б3=5 часов.
На изготовление этих изделий оборудование первого типа может работать не более чем t1=49 часов, оборудование второго типа не более чем t2=51 часов, оборудование третьего типа не более чем t3=45 часов.
Прибыль от реализации единицы готового изделия А составляет АЛЬФА=6 рублей, а изделия Б – БЕТТА=5 рублей.
Составить план производства изделий А и Б, обеспечивающий максимальную прибыль от их реализации.

Источник

Симплекс-метод, примеры решения задач

Здесь приведено ручное (не апплетом) решение двух задач симплекс-методом (аналогичным решению апплетом) с подробными объяснениями для того, чтобы понять алгоритм решения задач симплекс-методом. Первая задача содержит знаки неравенства только » ≤ » (задача с начальным базисом), вторая может содержить знаки » ≥ «, » ≤ » или » 2″>Симплекс-метод, решение задачи с начальным базисом

1)Симплекс-метод для задачи с начальным базисом (все знаки неравенств-ограничений » ≤ «).

Запишем задачу в канонической форме, т.е. ограничения-неравенства перепишем в виде равенств, добавляя балансовые переменные:

Эта система является системой с базисом (базис s₁, s₂, s₃, каждая из них входит только в одно уравнение системы с коэффициентом 1), x₁ и x₂ — свободные переменные. Задачи, при решении которых применяется симплекс-метод, должны обладать следующими двумя свойствами: -система ограничений должна быть системой уравнений с базисом; -свободные члены всех уравнений в системе должны быть неотрицательны.

Полученная система — система с базисом и ее свободные члены неотрицательны, поэтому можно применить симплекс-метод. Составим первую симплекс-таблицу (Итерация 0) для решения задачи на симплекс-метод, т.е. таблицу коэффициентов целевой функции и системы уравнений при соответствующих переменных. Здесь «БП» означает столбец базисных переменных, «Решение» — столбец правых частей уравнений системы. Решение не является оптимальным, т.к. в z – строке есть отрицательные коэффициенты.

Для улучшения решения перейдем к следующей итерации симплекс-метода, получим следующую симплекс-таблицу. Для этого надо выбрать разрешающий столбец, т.е. переменную, которая войдет в базис на следующей итерации симплекс-метода. Он выбирается по наибольшему по модулю отрицательному коэффициенту в z-строке (в задаче на максимум) – в начальной итерации симплекс-метода это столбец x₂ (коэффициент -6).

Затем выбирается разрешающая строка, т.е. переменная, которая выйдет из базиса на следующей итерации симплекс-метода. Она выбирается по наименьшему отношению столбца «Решение» к соответствующим положительным элементам разрешающего столбца (столбец «Отношение») – в начальной итерации это строка s₃ (коэффициент 20).

Разрешающий элемент находится на пересечении разрешающего столбца и разрешающей строки, его ячейка выделена цветом, он равен 1. Следовательно, на следующей итерации симплекс-метода переменная x₂ заменит в базисе s₁. Заметим, что в z-строке отношение не ищется, там ставится прочерк » — «. В случае если есть одинаковые минимальные отношения, то выбирается любое из них. Если в разрешающем столбце все коэффициенты меньше или равны 0, то решение задачи бесконечно.

Заполним следующую таблицу «Итерация 1». Её мы получим из таблицы «Итерация 0». Цель дальнейших преобразований — превратить разрешающий столбец х₂ в единичный (с единицей вместо разрешающего элемента и нулями вместо остальных элементов).

1)Вычисление строки х₂ таблицы «Итерация 1». Сначала делим все члены разрешающей строки s₃ таблицы «Итерация 0» на разрешающий элемент (он равен 1 в данном случае) этой таблицы, получим строку x₂ в таблице «Итерации 1». Т.к. разрешающий элемент в данном случае равен 1, то строка s₃ таблицы «Итерация 0» будет совпадать со строкой х₂ таблицы «Итерация 1». Строку x₂ таблицы «Итерации 1» мы получили 0 1 0 0 1 20, остальные строки таблицы «Итерация 1» будут получены из этой строки и строк таблицы «Итерация 0» следующим образом:

2) Вычисление z-строки таблицы «Итерация 1». На месте -6 в первой строке (z-строке) в столбце х₂ таблицы «Итерация 0» должен быть 0 в первой строке таблицы «Итерация 1». Для этого все элементы строки х₂ таблицы «Итерация 1» 0 1 0 0 1 20 умножим на 6, получим 0 6 0 0 6 120 и сложим эту строку с первой строкой (z — строкой) таблицы «Итерация 0» -4 -6 0 0 0 0, получим -4 0 0 0 6 120. В столбце x₂ появился ноль 0, цель достигнута. Элементы разрешающего столбца х₂ выделены красным цветом.

3) Вычисление строки s₁ таблицы «Итерация 1». На месте 1 в s₁ строке таблицы «Итерация 0» должен быть 0 в таблице «Итерация 1». Для этого все элементы строки х₂ таблицы «Итерация 1» 0 1 0 0 1 20 умножим на -1, получим 0 -1 0 0 -1 -20 и сложим эту строку с s₁ — строкой таблицы «Итерация 0» 2 1 1 0 0 64, получим строку 2 0 1 0 -1 44. В столбце х₂ получен необходимый 0.

4) Вычисление строки s₂ таблицы «Итерация 1». На месте 3 в s₂ строке таблицы «Итерация 0» должен быть 0 в таблице «Итерация 1». Для этого все элементы строки х₂ таблицы «Итерация 1» 0 1 0 0 1 20 умножим на -3, получим 0 -3 0 0 -3 -60 и сложим эту строку с s₁ — строкой таблицы «Итерация 0» 1 3 0 1 0 72, получим строку 1 0 0 1 -3 12. В столбце х₂ получен нужный 0. Столбец х₂ в таблице «Итерация 1» стал единичным, он содержит одну 1 и остальные 0.

Строки таблицы «Итерация 1» получаем по следующему правилу:

Новая строка = Старая строка – (Коэффициент разрешающего столбца старой строки)*(Новая разрешающая строка).

Например для z-строки имеем:

Старая z-строка (-4 -6 0 0 0 0) -(-6)*Новая разрешающая строка -(0 -6 0 0 -6 -120) =Новая z-строка (-4 0 0 0 6 120).

Для следующих таблиц пересчет элементов таблицы делается аналогично, поэтому мы его опускаем.

Источник