ЕГЭ по информатике 2022 — Задание 17 (Пишем программу)
Привет! Сегодня поговорим о 17 задании ЕГЭ по информатике 2022.
В 17 задании нужно считать числа из файла, проанализировать их и ответить на вопрос задачи.
Будем решать задание на языке Python.
Задача (Минимальное значение)
В файле содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от -10000 до 10000 включительно. Определите и запишите в ответе сначала количество пар элементов последовательности, в которых оба числа делятся нацело на 7, затем минимальную из сумм элементов таких пар. В данной задаче под парой подразумевается два подряд идущих элемента последовательности. Например для последовательности из пяти элементов: 7; 14; 21; -7; 4 — ответ 3 14.
Напишем программу на языке Python.
f=open('17_1.txt') count=0 sm=20000 n1=int(f.readline()) for s in f.readlines(): n2=int(s) if n1%7==0 and n2%7==0: count=count+1 sm=min(n1+n2, sm) n1=n2 print(count) print(sm)
В начале подвязываемся к файлу с помощью команды open().
Переменная count отвечает за количество пар, удовлетворяющих условию задачи. Переменная sm — это минимальная сумма элементов подходящих пар.
В начале в переменную sm кладём максимальное число, которое теоретически может получится (10000 + 10000). Это делается для того, чтобы это значение можно было легко «победить» при поиске минимального значения.
Затем считываем в переменную n1 первое число. C помощью конструкции » for s in f.readlines():» можно перебрать остальные числа из файла. В цикле считываем второе число для пары в переменную n2.
После того, как два числа у нас есть, мы анализируем эти элементы на условие задачи. Если одновременно два числа из пары делятся на 7, то мы подсчитываем такую пару.
Если пара подходит, то проверяем сумму элементов этой пары на минимальность. В переменную sm заносится минимальное значение из прежнего значения sm и претендующего нового значения n1+n2.
В конце цикла нужно переложить второе число в переменную n1, чтобы очередное число из файла считалось в переменную n2. Тем самым мы получим новую пару чисел.
Задача (Проверяем на что оканчивается число)
В файле содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от -10000 до 10000 включительно. Определите и запишите в ответе сначала количество пар элементов последовательности, в которых оба числа оканчиваются или на 3, или на 5 (можно неодновременно), затем максимальную из сумм элементов таких пар. В данной задаче под парой подразумевается два подряд идущих элемента последовательности. Например для последовательности из пяти элементов: 3; 15; 25; -3; 4 — ответ 3 40.
f=open('17_2.txt') count=0 sm=-20000 n1=int(f.readline()) for s in f.readlines(): n2=int(s) if (abs(n1)%10==3 or abs(n1)%10==5) and (abs(n2)%10==3 or abs(n2)%10==5): count=count+1 sm=max(n1+n2, sm) n1=n2 print(count) print(sm)
Т.к. мы ищем максимальную сумму, то в начале в переменную sm кладём наоборот минимальное значение (-10000-10000=-20000).
Когда ищем на что оканчивается положительное число, мы применяем конструкцию x%10. Т.е. находим остаток от деления на 10. Пример: 16 % 10 = 6. Но для отрицательных чисел это не работает -16 % 10 = 4. Почему такой ответ получается, можете посмотреть в этом видео: https://www.youtube.com/watch?v=BRfgE3pP0_c. Поэтому, чтобы правильно найти на что оканчивается число, применяем функцию abs(), что означает модуль числа.
Здесь мы должны логические выражения для первого и второго числа взять в скобки, потому что логическая операция И имеет приоритет перед ИЛИ.
В файле содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от -10000 до 10000 включительно. Определите и запишите в ответе сначала количество пар элементов последовательности, в которых хотя бы одно число является полным квадратом некоторого натурального числа, затем максимальную из сумм элементов таких пар. В данной задаче под парой подразумевается два подряд идущих элемента последовательности. Например для последовательности из пяти элементов: 9; 15; 23; -3; 4 — ответ 2 24.
f=open('17_3.txt') count=0 sm=-20000 n1=int(f.readline()) for s in f.readlines(): n2=int(s) if (n1>0 and (int(n1 ** 0.5) ** 2) == n1) or (n2>0 and (int(n2 ** 0.5) ** 2) == n2) : count=count+1 sm=max(n1+n2, sm) n1=n2 print(count) print(sm)
Здесь мы извлекаем корень из числа с помощью возведения в степень 0.5. Округляем результат в меньшую сторону с помощью функции int(). А затем снова возводим в квадрат. Если мы получили изначальное число, значит, это число и есть полный квадрат некоторого натурального числа.
Возведение в степень в 0.5 работает и для отрицательных чисел. Т.к. в задаче имеют ввиду квадраты натуральных чисел, то мы работаем только с числами, которые больше нуля.
В файле 17-3.txt содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от -10 000 до 10 000 включительно. Определите и запишите в ответе сначала количество троек элементов последовательности, в которых числа расположены в порядке возрастания, затем минимальную из разностей наибольшего и наименьшего элементов таких троек. В данной задаче под тройкой подразумевается три идущих подряд элемента последовательности.
f=open('17-3.txt') count=0 rz=20000 n1=int(f.readline()) n2=int(f.readline()) for s in f.readlines(): n3 = int(s) if n1 < n2 < n3: count=count+1 mx = max(n1, n2, n3) mn = min(n1, n2, n3) rz = min(rz, mx-mn) n1=n2 n2=n3 print(count, rz)
С тройками решаем аналогично. До цикла считываем два числа. Внутри цикла считываем третье число.
В конце цикла перекладываем числа: второе число в n1, третье число в n2.
Задача (Любой порядок элементов)
В файле содержится последовательность из 10 000 целых положительных чисел. Каждое число не превышает 10 000. Определите и запишите в ответе сначала количество пар элементов последовательности, у которых сумма элементов кратна 9, затем максимальную из сумм элементов таких пар. В данной задаче под парой подразумевается два различных элемента последовательности. Порядок элементов в паре не важен.
f = open('17.txt') count_0 = 0 count_1 = 0 count_2 = 0 count_3 = 0 count_4 = 0 count_5 = 0 count_6 = 0 count_7 = 0 count_8 = 0 mx1_0 = 0 mx2_0 = 0 mx_1 = 0 mx_2 = 0 mx_3 = 0 mx_4 = 0 mx_5 = 0 mx_6 = 0 mx_7 = 0 mx_8 = 0 for s in f.readlines(): n=int(s) if n%9==0: count_0 = count_0 + 1 if n>mx1_0: if n>mx2_0: mx1_0 = mx2_0 mx2_0 = n else: mx1_0 = n if n%9==1: count_1 = count_1 + 1 mx_1 = max(mx_1, n) if n%9==2: count_2 = count_2 + 1 mx_2 = max(mx_2, n) if n%9==3: count_3 = count_3 + 1 mx_3 = max(mx_3, n) if n%9==4: count_4 = count_4 + 1 mx_4 = max(mx_4, n) if n%9==5: count_5 = count_5 + 1 mx_5 = max(mx_5, n) if n%9==6: count_6 = count_6 + 1 mx_6 = max(mx_6, n) if n%9==7: count_7 = count_7 + 1 mx_7 = max(mx_7, n) if n%9==8: count_8 = count_8 + 1 mx_8 = max(mx_8, n) count = (count_1*count_8) + (count_2*count_7) + (count_3*count_6) + (count_4*count_5) + (count_0*(count_0-1)//2) mx = max(mx_1 + mx_8, mx_2 + mx_7, mx_3 + mx_6, mx_4 + mx_5, mx1_0 + mx2_0) print(count, mx)
Здесь мы ищем количество элементов, у которых остаток при делении на 9 равен нулю, единице, двойке, . и до 8. Подсчитываем эти данные соответственно в переменные count_0, count_1, count_2 . и т.д.
Так же находим максимальное число, которое имеет при делении на 9 остаток равный единице, двойке, . и т.д. Для чисел, которые имеют остаток при делении на 9 ноль, находим два максимальных числа.
После того, как результаты находятся в нужных переменных, можно вычислить ответ к задаче.
Если, к примеру, взять число для которого остаток равен 1 и число для которого остаток равен 8, то их сумма будет делится на 9. Найдём количество пар, если нам известно количество и тех, и тех чисел.
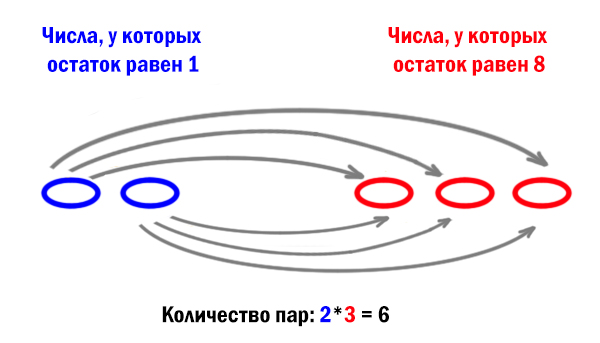
Значит, просто нужно перемножить два числа, к примеру, count_1*count_8.
Для чисел, которые делятся на 9 (т.е. остаток равен нулю), количество пар считается немного по-другому. Такие числа можно суммировать между собой, всё равно сумма тоже будет делится на 9. Путь есть у нас количество чисел count_0, которые делятся на 9. Тогда найдём количество пар, которые можно составить из этих элементов.
Здесь вспомним метод умножения, о котором было написано в этой статье.
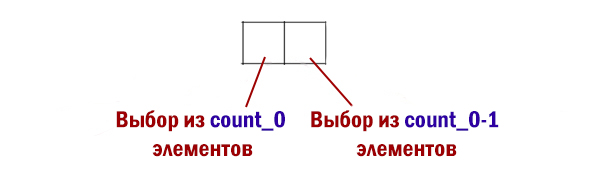
Найдём количество таких пар, если каждый элемент можно использовать 1 раз. Получается count_0*(count_0-1). Но т.к. в нашем случае пара, когда элементы находятся в одном порядке и в обратном, является одной и той же, то нужно это количество поделить на 2. Т.е количество пар будет (count_0*(count_0-1))/2.
f = open('17.txt') count=0 mx=0 a = [] #Считываем все числа в массив a for s in f.readlines(): n = int(s) a.append(n) # Перебираем все варианты и подсчитываем пары, отвечающие условию задачи. for i in range(0, len(a)): for j in range(i+1, len(a)): if (a[i]+a[j])%9==0: count = count + 1 mx = max(a[i]+a[j], mx) print(count, mx)
В этом решении сначала считываем все числа в массив a.
Далее берём число и начинаем его комбинировать со всеми числами, которые стоят после этого числа. Таким образом, мы переберём все возможные комбинации, и у нас не будут пары повторяться.
Задание 17 ЕГЭ по информатике и примеры решения на Python (задания _ Евич Информатика Подготовка к ЕГЭ 2023 14 тренировочных варианта по демоверсии 2023 г)

f=open(’17_1.txt’)
a=[int(x) for x in f]
minimum=min(a)
k=0
max_summa=0
s1=0
k1=0
for i in range(len(a)):
if a[i]%4==0:
s1+=a[i]
k1+=1
sr_ar=s1/k1
for i in range(len(a)-1):
if (a[i]%minimum==0 and a[i]+a[i+1]or (a[i+1]%minimum==0 and a[i]+a[i+1] k=k+1
max_summa=max(max_summa,a[i]+a[i+1])
print(k,max_summa)
f=open(’17_2.txt’)
a=[int(x) for x in f]
maximum=max(a)
k=0
min_summa=10000000000000
s1=0
k1=0
for i in range(len(a)):
if a[i]%10==3:
s1+=a[i]
k1+=1
sr_ar=s1/k1
for i in range(len(a)-1):
if (maximum%a[i]==0 and a[i]+a[i+1]sr_ar) or (maximum%a[i+1]==0 and a[i]+a[i+1]sr_ar):
k=k+1
min_summa=min(min_summa,a[i]+a[i+1])
print(k,min_summa)
f=open(’17_3.txt’)
a=[int(x) for x in f]
k=0
max_summa=0
for i in range(len(a)-1):
if a[i]%5==0 and a[i+1]%5==0:
k=k+1
max_summa=max(max_summa,a[i]+a[i+1])
print(k,max_summa)
Ответ: 213 965
f=open(’17_4.txt’)
a=[int(x) for x in f]
k=0
min_summa=10000000000000
for i in range(len(a)-1):
if a[i]%20 or a[i+1]%20:
k=k+1
min_summa=min(min_summa,a[i]+a[i+1])
print(k,min_summa)
def h(ch):
k6 = 0
while ch0:
ost=ch%10
if ost==6:
k6=k6+1
ch=ch//10
return k6
f=open(’17_5.txt’)
a=[int(x) for x in f]
k=0
m=1000000000000000
for i in range(len(a)):
if h(abs(a[i]))0:
k=k+1
m=min(a[i],m)
print(k,m)
def h(ch):
k4 = 0
while ch0:
ost=ch%10
if ost==4:
k4=k4+1
ch=ch//10
return k4
f=open(’17_6.txt’)
a=[int(x) for x in f]
k=0
m=0
for i in range(len(a)):
if h(abs(a[i]))0:
k=k+1
m=max(a[i],m)
print(k,m)
f=open(’17_7.txt’)
a=[int(x) for x in f]
k=0
max_razn=0
for i in range(len(a)-1):
if a[i]a[i+1]:
k=k+1
max_razn=max(max_razn,a[i]-a[i+1])
print(k,max_razn)
f=open(’17_8.txt’)
a=[int(x) for x in f]
k=0
min_razn_kv=100000000000
for i in range(len(a)-1):
if a[i]0 and a[i+1]0 and a[i+1]a[i]:
k=k+1
min_razn_kv=min(min_razn_kv,a[i+1]**2-a[i]**2)
print(k,min_razn_kv)
f=open(’17_9.txt’)
a=[int(x) for x in f]
m=0
k=0
for i in range(len(a)):
if a[i]%4==0 and a[i]%5!=0 and a[i]%8!=0 and a[i]%31!=0 and a[i]%41!=0:
k=k+1
m=max(m,a[i])
print(m,k)
f=open(’17_10.txt’)
a=[int(x) for x in f]
m=100000000000
k=0
for i in range(len(a)):
if a[i]%7==0 and a[i]%5==0 and a[i]%2!=0 and a[i]%11!=0 and a[i]%91!=0:
k=k+1
m=min(m,a[i])
print(m,k)
f=open(’17_11.txt’)
a=[int(x) for x in f]
k=0
b=[]
for i in range(len(a)):
if a[i]%2==0 and a[i]%30:
k=k+1
b.append(a[i])
b.sort(reverse=True)
print(k,b[1])
Ответ: 1299 9664
f=open(’17_12.txt’)
a=[int(x) for x in f]
k=0
b=[]
for i in range(len(a)):
if a[i]%3==0 and a[i]%20:
k=k+1
b.append(a[i])
b.sort()
print(k,b[1])
f=open(’17_13.txt’)
a=[int(x) for x in f]
k=0
m=100000000000000000
a=a[1:]
a=a[:-1]
for i in range(len(a)-2):
if a[i+1]a[i] and a[i+1]a[i+2]:
k=k+1
m=min(m,a[i+1])
print(k,m)
f=open(’17_14.txt’)
a=[int(x) for x in f]
k=0
m=0
a=a[1:]
a=a[:-1]
for i in range(len(a)-2):
if a[i+1]or a[i+1]2] or a[i+1]and a[i+1]2]:
k=k+1
m=max(m,a[i+1])
print(k,m)


















