ЕГЭ по информатике 2022 — Задание 16 (Рекурсия)
Шестнадцатое задание из ЕГЭ по информатике 2022 даётся на рекурсию.
Это задание нужно делать с помощью компьютера.
В программировании рекурсией называется процесс, когда функция вызывает сама себя или, когда две функции попарно вызывают друг друга.
Мы будем писать все программы на языке программирования Python.
Что такое Функция в языке программирования Python ?
Рассмотрим пример функции, которая суммирует два числа!
def F(x, y): s = x + y return s a = int(input()) b = int(input()) r = F(a, b) print(r)
Здесь функция F, которая суммирует два числа.
В главной части программы запрашиваются два числа с клавиатуры: a и b! Эти два числа передаются в функцию F. В функции эти числа кладутся в локальные переменные x и y. Сумма переменных x и y записывается в переменную s. Переменная s возвращается, как результат работы функции F.
Результат работы функции будет помещён в переменную r (в строке r = F(a, b)) в основной части программы.
Таким образом, в переменной r будет сумма двух переменных a и b.
Функции позволяют сократить программный код для однотипных расчётов.
Тренировочные задачи 16 задания из ЕГЭ по информатике 2023
Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = 1 при n = 1;
F(n) = n + F(n − 1), если n – чётно,
F(n) = 3 × F(n − 2), если n > 1 и при этом n – нечётно.
Чему равно значение функции F(25)?
Напишем программу для решения данной задачи. В начале опишем все правила, которые даны в условии задачи для функции. В основной части программы запустим эту функцию.
# Сама функция def F(n): if n==1: return 1 if n%2==0: return n+F(n-1) if n>1 and n%2!=0: return 3*F(n-2) # Основная часть программы print(F(25))
После запуска рекурсивной функции программа выведет ответ 531441.
Выражение n%2 != 0 (остаток от деления на «2» не равен нулю) обозначает нечётное число. Выражение n%2==0 обозначает чётное число.
Продолжаем тренировку по подготовке к 16 заданию ЕГЭ по информатике 2022.
Задача (Продолжаем подготовку)
Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(1) = 1
F(2) = 3
F(n) = F(n–1) * n + F(n–2) * (n – 1) , при n > 2
Чему равно значение функции F(8)? В ответе запишите только натуральное число.
# Сама функция def F(n): if n==1: return 1 if n==2: return 3 if n>2: return F(n-1)*n + F(n-2)*(n-1) # Основная часть программы print(F(8))
Ответ получается 148329.
Закрепляющий пример на рекурсию 16 задания из ЕГЭ по информатике 2022.
Алгоритм вычисления значения функций F(n) и G(n), где n — натуральное число, задан следующими соотношениями:
Чему равно значение функции F(8)? В ответе запишите только натуральное число.
# Сами функции def F(n): if nreturn 0 if n>2: return G(n-2) def G(n): if nreturn 0 if n>1: return F(n-1)+n # Основная часть программы print(F(8))
Задача (Количество значений)
Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = 2*n*n*n + 1, при n > 25
F(n) = F(n+2) + 2*F(n+3), при n ≤ 25
Определите количество натуральных значений n из отрезка [1; 1000], для которых значение F(n) кратно 11.
# Сама функция def F(n): if n>25: return 2*n*n*n + 1 if nreturn F(n+2) + 2*F(n+3) k=0 # Перебираем диапазон for i in range(1, 1001): if F(i)%11==0: k=k+1 print(k)
В начале формируем функцию F. Затем перебираем числа из диапазона от 1 до 1000. Каждое число подставляем в функцию F. Если значение функции F делится на 11, то мы зачитываем такое значение i.
Задача (Используем глобальную переменную)
Решение:
При решении этой задачи можно применить глобальную переменную.
def F(n): global s s=s+1 if n>=1: s=s+1 F(n-1) F(n-2) s=s+1 s=0 F(35) print(s)
Здесь внутри функции заводим глобальную переменную s, которая будет подсчитывать количество напечатанных звёздочек. Теперь эту переменную видно при любом вызове функции, и при каждом вызове функции она будет одна и та же переменная. Вместо печати звёздочек пишем конструкцию s=s+1.
В основной части программы перед первым запуском функции переменной s присваиваем 0.
Программа может немного медленно работать из-за большой глубины рекурсии, но через минуту выведет число 96631265.
Новые тенденции
В последнее время мы видим тенденцию в 16 задании из ЕГЭ по информатике 2023, что теперь мало переписать функцию и её запустить. Необходимо подумать, как можно преобразовать то рекурсивное выражение, которое нужно вычислить.
(К. Багдасарян) Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = 2, если n = 1,
F(n) = 2 · F(n – 1), если n > 1.
Чему равно значение выражения F(1900)/2 1890 ?
1 Способ (Аналитическое решение)
Если мы просто перепишем функцию и попытаемся вычислить выражение F(1900)/2 1890 , то получим ошибку RecursionError: maximum recursion depth exceeded . Возникает она из-за слишком большой цепочки вызовов функции.
В подобных задачах нужно попытаться самому упростить выражение, которое пытаемся вычислить. Посмотрим, что из себя представляет функция.
F(1900) = 2*F(1899) = 2*2*F(1898) = . 2 1900
F(1900)/2 1890 = 2 1900 /2 1890 = 2 10 = 1024
Чтобы уменьшить цепочку вызовов функции, можно использовать инструмент lru_cache.
from functools import lru_cache @lru_cache(None) def F(n): if n==1: return 2 if n>1: return 2*F(n-1) for i in range(2, 1900): F(i) print(F(1900)/2**1890)
В задаче функция опирается на значение функции от n-1 и т.д. За счёт этого происходят длинные вычисления для каждого числа n.
Использовав инструмент lru_cache, мы пробегаемся в цикле по значениям n в возрастающем порядке, и для каждого значения сохраняем результаты функции. Таким образом, вычисляя очередное значение, программа опирается на уже готовый результат, тем самым цепочка вызовов функции будет маленькой.
Задача(Новое веяние, закрепление)
Алгоритм вычисления значения функции F(n), где n — натуральное число, задан следующими соотношениями:
F(n) = 1 при n ≤ 2;
F(n) = n * F(n-2), если n > 2.
Чему равно значение выражение F(3000)/F(2996) ?
1 Способ (Аналитическое решение)
F(3000) = 3000*F(2998) = 3000*2998*F(2996)
F(3000)/F(2996) = 3000*2998*F(2996)/F(2996) = 3000*2998 = 8994000
from functools import lru_cache @lru_cache(None) def F(n): if nreturn 1 if n>2: return n*F(n-2) for i in range(2, 3000): F(i) print(F(3000)/F(2996))
Задача (Вперёд к победе!)
Алгоритм вычисления значения функции F(n), где n — натуральное число, задан следующими соотношениями:
F(n) = 1 при n=1;
F(n) = 2 при n=2;
F(n) = n*(n-1) + F(n-1) + F(n-2), если n > 2.
Чему равно значение функции F(2023) — F(2021) — 2*F(2020) — F(2019)?
1 Способ (Аналитическое решение)
F(2023) = 2023*2022 + F(2022) + F(2021) =
= 2023*2022 + 2022*2021 + F(2021) + F(2020) + F(2021) =
=2023*2022 + 2022*2021 + 2021*2020 + F(2020) + F(2019) + F(2020) + F(2021) =
2023*2022 + 2022*2021 + 2021*2020 + 2*F(2020) + F(2019) + F(2021) =
2023*2022 + 2022*2021 + 2021*2020 + F(2021) + 2*F(2020) + F(2019)
Если подставим полученный результат в выражение, которое нужно найти, то получим:
2023*2022 + 2022*2021 + 2021*2020 = 12259388
from functools import lru_cache @lru_cache(None) def F(n): if n==1: return 1 if n==2: return 2 if n>2: return n*(n-1) + F(n-1) + F(n-2) for i in range(2, 2023): F(i) print(F(2023) - F(2021) -2*F(2020) - F(2019))
Удачи при решении 16 задания из ЕГЭ по информатике 2022.
Студия Компьютерного Мастерства
Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = 1 при n = 1;
F(n) = n × F(n − 1), если n > 1.
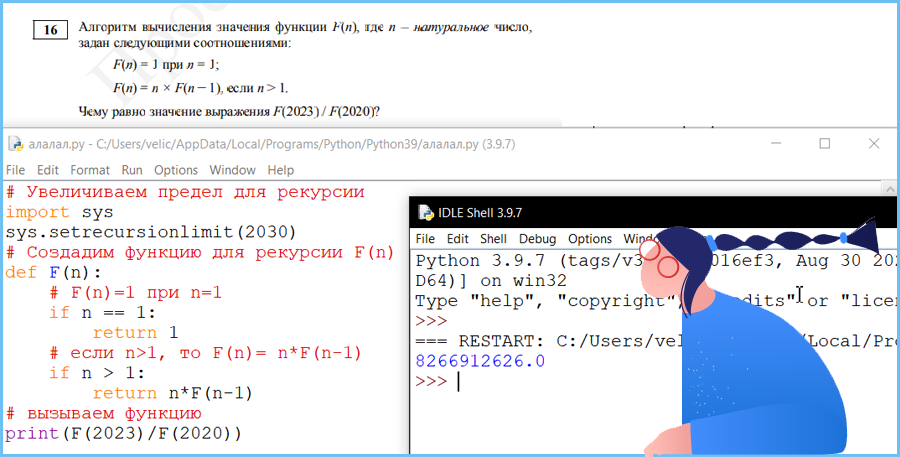
Чему равно значение выражения F(2023) / F(2020)?
Вариант программы 1
Лимит рекурсии по умолчанию в Python является 1000, вы получите ошибку « RecursionError: максимальная глубина рекурсии превышена в сравнении »
Это может быть исправлено, увеличивая предел рекурсиона в Python, ниже – фрагмент о том, как вы можете увеличить предел рекурсии.
import sys
sys.setrecursionlimit(2030)
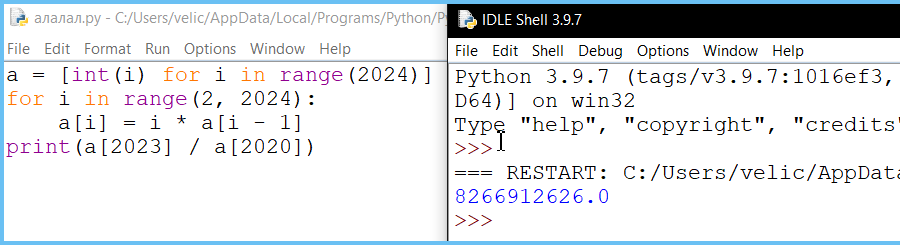
Вариант программы 2
Алгоритмы, опирающиеся на несколько предыдущих значений
Задание 6 (Решу ЕГЭ)
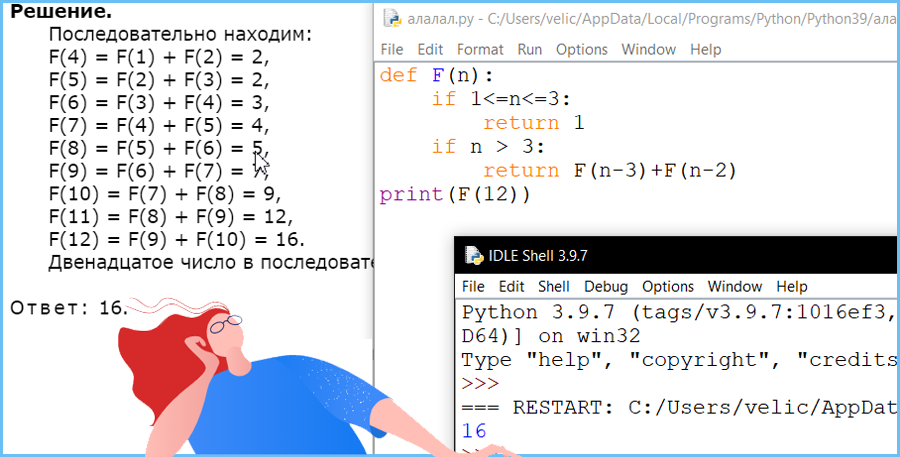
Последовательность чисел Падована задается рекуррентным соотношением:
F(n) = F(n–3) + F(n–2), при n >3, где n – натуральное число.
Чему равно двенадцатое число в последовательности Падована?
В ответе запишите только натуральное число.
Задание 6 (Решу ЕГЭ)
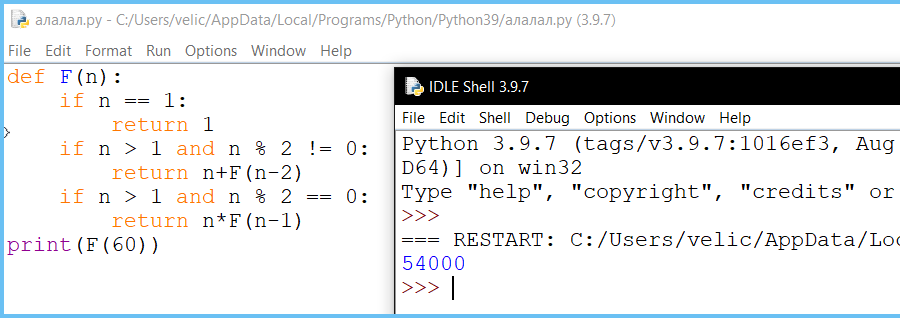
Алгоритм вычисления значения функции F(n), где n — натуральное число, задан следующими соотношениями:
F(n) = n + F(n − 2), если n — нечётно, и n > 1;
F(n) = n × F(n − 1), если n — чётно.
Чему равно значение функции F(60)?
Алгоритмы, опирающиеся на несколько предыдущих значений
Задание 6 (Решу ЕГЭ)
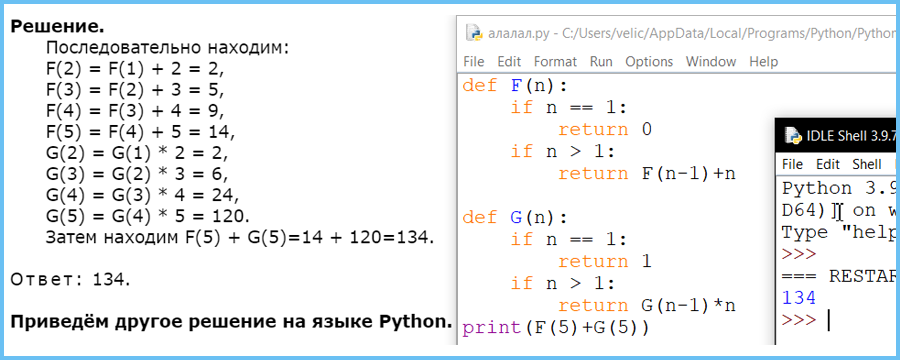
Алгоритм вычисления значения функции F(n) и G(n), где n – натуральное число, задан следующими соотношениями:
Чему равно значение функции F(5) + G(5)?
В ответе запишите только натуральное число.
Сложные задачи
Задание 6 (Поляков ЕГЭ)
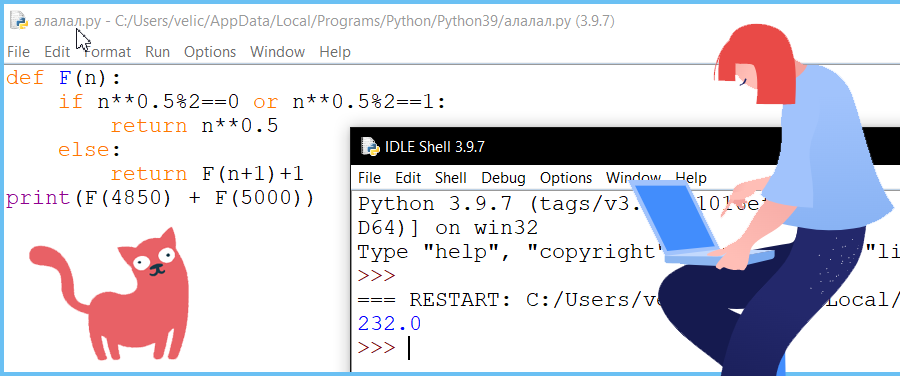
(№ 5604) (А. Куканова) Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями: F(n) = sqrt(n), если sqrt(n) – натуральное число, F(n) = F(n + 1) + 1, если sqrt(n) – дробное число. Чему равно значение выражения F(4850) + F(5000)?
При делении натурального числа на 2 мы получаем в остатке (%) или 0 или 1 (чётные и нечётные числа), таким образом проверяем, если корень дает четное или нечётное целое число, то выводим корень этого числа во всех остальных случаях применяет функцию F(n+1)+1
sqrt(n) запишем как n**0.5, что бы не подключать дополнительный математический модуль из библиотеки
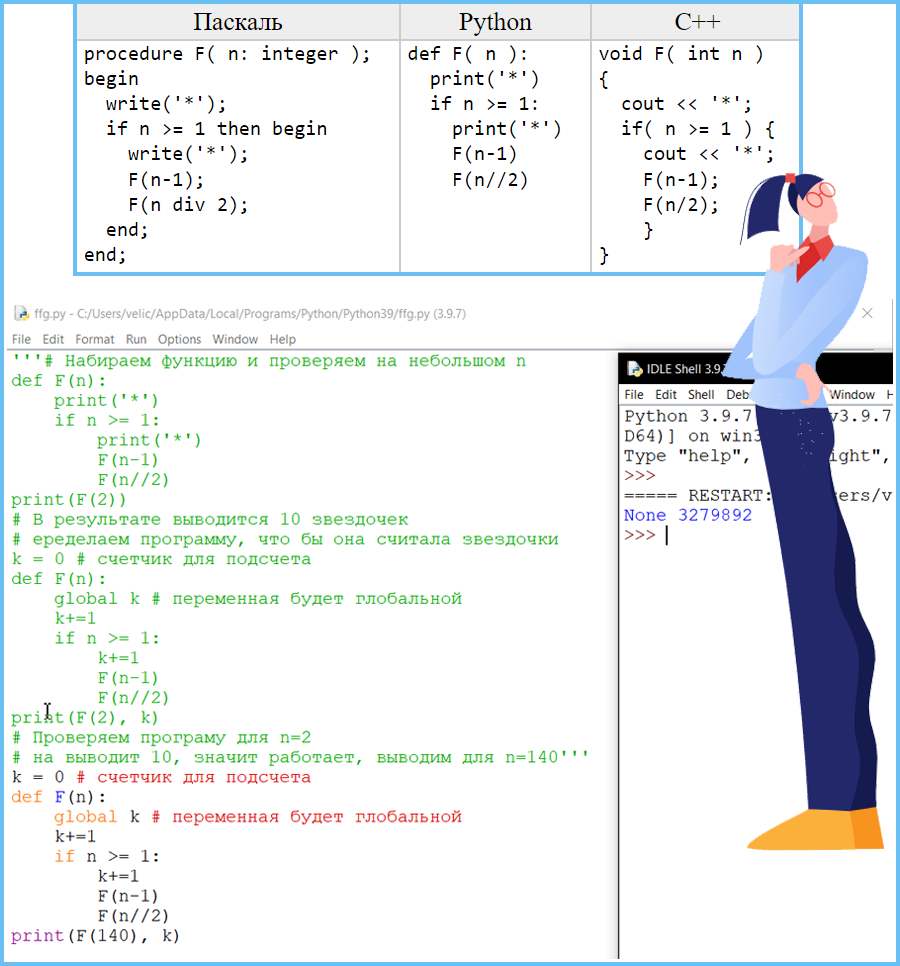
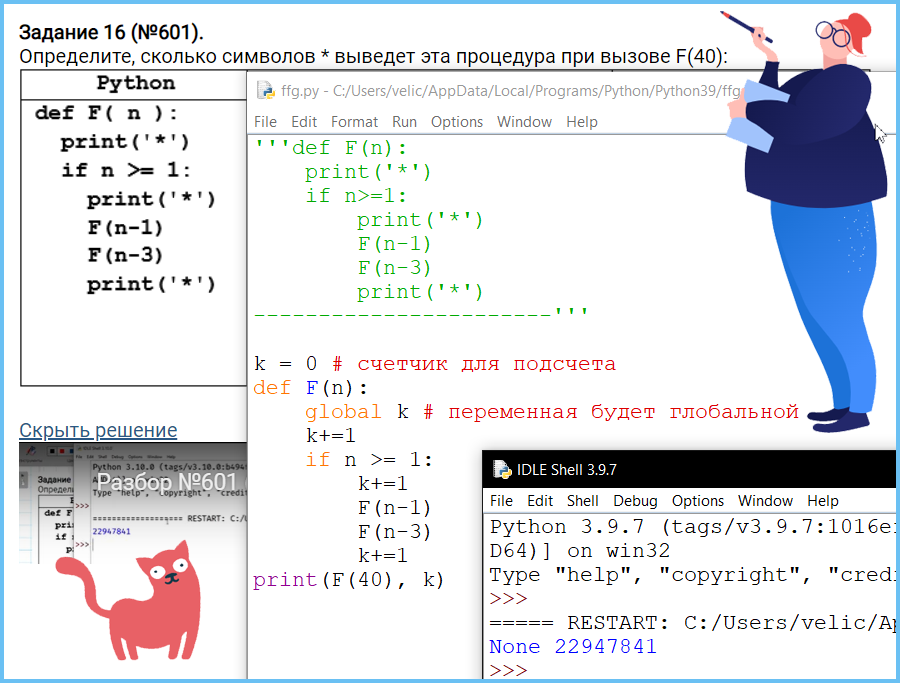
Задание 6 (Поляков ЕГЭ)
Определите, сколько символов * выведет эта процедура при вызове F(140):
Алгоритмы, опирающиеся на несколько предыдущих значений
Задание 6 (Поляков ЕГЭ)
(№ 5604) (А. Куканова) Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = n!, если n ≥ 5000,
F(n) = 2 · F(n + 1) / (n + 1), если 1 ≤ n < 5000.
Чему равно значение выражения 1000 · F(7) / F(4)? Примечание.
Факториал числа n, который обозначается как n!, вычисляется по формуле n!=1·2·…·n.
Модуль math – один из наиважнейших в Python. Этот модуль предоставляет обширный функционал для проведения вычислений с вещественными числами (числами с плавающей точкой). Для использования этих функций в начале программы необходимо подключить модуль, что делается командой import:
# программный код
import math
num1 = math.sqrt(2) # вычисление корня квадратного из двух
Как можно заметить из примера выше, для вызова функции мы вынуждены указывать название модуля и символ точки. С другой стороны, если функции используются достаточно часто, то такой вызов (постоянное указание названия модуля и символа точки) может усложнить программу и сделать её менее читабельной. Для того, чтобы не указывать название модуля и символ точки при вызове функций, мы пишем следующий код:
# программный код
from math import *
Если нужно использовать только некоторые функции модуля, то мы можем импортировать только их следующим образом: from math import sqrt, ceil, factorial