Рекуррентные соотношения программирование примеры

Понятие рекурсии и простейшие рекурсивные алгоритмы. Примеры задач. Рекурсивные алгоритмы и их построение

Рекурсивная функция (лат. recursio — возвращение) — функция, которая в своей записи содержит вызов себя же.

Рекуррентные отношения

Фракталы и фрактальные множества

Помните детское стихотворение-считалку про 10 негритят? Оно может служить эпиграфом к любой работе на тему «Рекурсия».

«10 негритят пошли купаться в море, 10 негритят резвились на просторе, Один из них пропал – и вот вам результат: 9 негритят пошли купаться в море, 9 негритят резвились на просторе, Один из них пропал – и вот вам результат: … … … … … 1 (из) негритят пошли(ел) купаться в море, 1 (из) негритят резвились(ся) на просторе, Один из них пропал – и вот вам результат: Нет больше негритят!»

Первые три строчки этого стихотворения повторяются 10 раз с небольшим изменением — число негритят уменьшается с каждым разом на единицу. И только, когда число негритят уменьшилось до нуля, стихотворение заканчивается единственной строчкой «Нет больше негритят!». Напишем процедуру, печатающую это стихотворение.

procedure Negr(k: integer); begin if k=0 then Writeln('Нет больше негритят!') else begin Writeln(k,' негритят пошли купаться в море,'); Writeln(k,' негритят резвились на просторе,'); Writeln('Один из них пропал - и вот вам результат:'); Negr(k-1); end end;

Вызов этой процедуры в основной программе будет выглядеть так: Negr(10).

Интересным является применение рекурсии при создании рисунков.

Пример 1 .

Рассмотрим простейший рисунок из окружностей разных радиусов.

Если вглядеться в него внимательно, то можно заметить, что рисунок начинается с центральной окружности самого большого радиуса. Затем осуществляется переход на концы горизонтального диаметра окружности, которые должны играть роль центров двух окружностей меньшего радиуса (примерно в полтора раза). Этот же процесс повторяется и с этими двумя окружностями, и с полученными четырьмя новыми, и так далее до тех пор, пока уменьшающийся радиус окружности не станет меньше первоначального в 1,5*1,5*1,5*1,5 раз (если посчитать, то должно выполниться четыре вложенных вызова рекурсивной процедуры).

Рекурсивная процедура, выполняющая такой рисунок, должна иметь в качестве передаваемых параметров координаты центра окружности и величину радиуса.

Программа, при помощи которой будет нарисован этот рисунок, может быть написана так:

uses Graph; procedure Ris(x,y,r:integer); begin If r>=10 then begin Circle(x,y,r); < Рисуем окружность > < Вызываем 2 раза рекурсивно саму себя >Ris(x-r,y,r*2 div 3); Ris(x+r,y,r*2 div 3) end end; var GD,GM : integer; begin GD := detect; GM := 1; InitGraph(GD,GM,''); Ris(320,240,100); < Рисуем по центру экрана, самая большая окружность - 100 пикселей >Readln; CloseGraph; end.

Реализация на Delphi с сохранением в файл.

unit MainUnit; interface uses Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics, Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.ExtCtrls, PngImage; type TDrawForm = class(TForm) Image: TImage; procedure FormCreate(Sender: TObject); private procedure SaveToPNG(FileName: string); procedure Circle(x, y, r: integer); procedure Ris(x, y, r: integer); public end; var DrawForm: TDrawForm; implementation procedure TDrawForm.FormCreate(Sender: TObject); begin < Не закрашивать фигуру >Image.Canvas.Brush.Style := bsClear; < Подстройка ширины и высоты картинки >Image.Width := 559; Image.Height := 220; Image.Picture.Bitmap.Width := Image.Width; Image.Picture.Bitmap.Height := Image.Height; < Вызов рекурсивной процедуры >Ris(Image.Width div 2, Image.Height div 2, 100); < Сохранение в формате .png >SaveToPNG('ris.png'); end; < Сохранение в формате .png: FileName - имя файла >procedure TDrawForm.SaveToPNG(FileName: string); var png: TPngImage; begin png := TPngImage.Create; png.Assign(Image.Picture.Bitmap); png.SaveToFile(FileName); png.Free; end; < Окружность с центром: x, y - центр окружности, r - радиус >procedure TDrawForm.Circle(x, y, r: integer); begin Image.Canvas.Ellipse(x - r, y - r, x + r, y + r); end; < Рекурсивная процедура >procedure TDrawForm.Ris(x, y, r: integer); begin if r >= 15 then begin Circle(x, y, r); Ris(x - r, y, r * 2 div 3); Ris(x + r, y, r * 2 div 3) end; end; end.

Пример 2.

На входном потоке находится слово (последовательность литер), заканчивающаяся пробелом. Написать программу, которая позволит напечатать это слово «задом наперед», т.е. выписывая буквы слова с конца.

В этом примере мы опишем процедуру, у которой не будет параметров, т.к. при каждом ее вызове будет вводиться одна литера, которая будет сравниваться с пробелом. Сама же программа будет состоять только из вызова этой процедуры.

Procedure REV; var c:char; begin read(c); if c<>' ' then begin REV; write(c) end end; BEGIN REV END.

Фракталы

Фракталами называются множества, части которых являются повторением образов самих множеств. Изображения фракталов вызывают обычно у всех большой интерес.

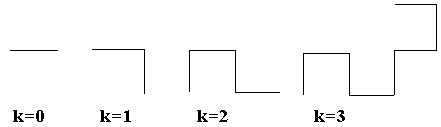
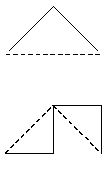
Рассмотрим процесс сгибания бумажной полоски: если взять полоску бумаги, согнуть ее пополам К раз и развернуть полоску так, чтобы углы на сгибах стали равны 90°, то, посмотрев на торец полоски, можно увидеть ломаную, которая называется «драконовой ломаной К-го порядка», где K-количество сгибов. Схема этого процесса изображена ниже.

Опишем способ создания «драконовой» ломаной.

На ломаной нулевого порядка, как на гипотенузе, строим прямой угол, на полученных сторонах прямого угла строим тоже прямые углы, но один развернут в правую сторону, а другой — в левую. Данный процесс повторяется К раз.

Напишем соответствующую программу, которая по заданному числу К рисует драконову ломаную К-го порядка.

Program DRACON;

Uses Graph;

Var Gd,Gm,k:Integer;

Procedure st (x1, y1, x2, y2, k:Integer);

Var xn,yn:Integer;

Beg in

xn:=(x1+x2) div 2 + (y2-y1)div 2;

yn:=(y1+y2) div 2 — (x2-x1)div 2;

else Line(x1,y1,x2,y2);

WriteLn (‘Введите номер уровня ‘);

Если с помощью этой программы построить ломаную дракона 14-го порядка, то мы получим образ множества, называемого фракталом Хартера-Хейтуэя, рисунок которого приведен ниже.

Литература

Павлова М.В., Паньгина Н.Н. Примеры и задачи на тему «Рекурсия». – «Компьютерные инструменты в образовании», 2001

Источник

Рекурсия

Рекурсия — состоит в определении, описании, изображении какого-либо объекта или процесса внутри самого этого объекта или процесса. Это ситуация, когда объект является частью самого себя.

Процедура или функция может содержать вызов других процедур или функций. В том числе процедура может вызвать саму себя. Компьютер лишь последовательно выполняет команды и, если встречается вызов процедуры, просто начинает выполнять эту процедуру. Без разницы, какая процедура дала команду это делать.

#include
using namespace std;
void func( int num)
if (num > 0) func(num — 1);
cout >
int main()
func(3);
cin.get(); return 0;
>

Процедура func() вызывается с параметром 3. В ней содержится вызов процедуры func() с параметром 2. Предыдущий вызов еще не завершился, поэтому создается еще одна процедура и до окончания ее работы func(3) свою работу приостанавливает. Процесс вызова заканчивается, когда параметр равен 0. В этот момент одновременно выполняются 4 экземпляра процедуры.

Количество одновременно выполняемых процедур называют глубиной рекурсии .

Последняя вызванная процедура func(0) выведет число 0 и закончит свою работу. После этого управление возвращается к процедуре, которая ее вызвала: func(1) и выводится число 1. И так далее пока не завершатся все процедуры.

Важным и обязательным моментом в формировании рекурсивной процедуры является базис рекурсии. Базис рекурсии определяет условие выхода из рекурсии. Как правило, в качестве базиса записывается некий простейший случай, при котором ответ получается сразу, без использования рекурсии.
Существует такое понятие как шаг рекурсии или рекурсивный вызов . В случае, когда рекурсивная функция вызывается для решения сложной задачи (не базового случая) выполняется некоторое количество рекурсивных вызовов или шагов, с целью сведения задачи к более простой. И так до тех пор пока не получим базовое решение.

Сложная рекурсия

Возможна чуть более сложная схема: функция A вызывает функцию B, а та в свою очередь вызывает A. Это называется сложной рекурсией . При этом оказывается, что описываемая первой процедура должна вызывать еще не описанную. Чтобы это было возможно, требуется использовать описание функции B до ее использования.
Пример : вычислить значение выражения

#include
using namespace std;
int pow( int , int ); // описание сигнатуры
double calc( int x, int n)
return ( double )pow(x, n) / n; // вызов функции pow
>
int pow( int x, int n)
if (n == 1) return x;
return x*calc(x, n — 1); // вызов функции calc
>
int main()
int n, x;
cout > n;
cout > x;
double a = calc(x, n); // вызов рекурсивной функции
cout cin.get(); cin.get();
return 0;
>

Результат выполнения

Префиксная и постфиксная форма записи

Если процедура вызывает сама себя, то, по сути, это приводит к повторному выполнению содержащихся в ней инструкций, что аналогично работе цикла. При этом различают префиксную и постфиксную формы записи.

Источник

Рекурсия и рекуррентные соотношения

Рекурсия, как альтернатива циклу, является одним из полезных средств в арсенале программиста, но содержит в себе «подводные камни». Попробуем разобраться, когда она бывает эффективна.

Простейший пример рекуррентного соотношения: F(0)=1, F(1)=1*F(0), F(2)=2*F(1), … , F(n)=n*F(n-1). Как Вы понимаете, это вычисление факториала. Но можно эти соотношения записать короче: F(n)=n*F(n-1) для n=1,2,…,N, причем F(0)=1.

Рекуррентные соотношения могут быть реализованы как через цикл (от начала к концу), так и через рекурсию (от конца к началу). Часто используют такие структуры данных, для которых целесообразно применять рекурсивные методы при написании программ.

Рекурсивные методы удобны при работе с рекурсивными структурами данных — списками, деревьями.

Примеры применения рекурсивных методов: вычисление факториала, Ханойские башни, закрашивание замкнутой области (см. ниже), подсчет числа слов в тексте, поиск пути в лабиринте, обход деревьев, обработка списков.

Необходимые определения

Метод P называется рекурсивным, если при выполнении тела метода происходит вызов метода P.
Рекурсия может быть прямой, если вызов P происходит непосредственно в теле метода P.
Рекурсия может быть косвенной, если в теле P вызывается метод Q (эта цепочка может быть продолжена), в теле которого вызывается метод P.
Важно! Для того чтобы рекурсия не приводила к зацикливанию, в тело нормального рекурсивного метода всегда встраивается оператор выбора, одна из ветвей которого не содержит рекурсивных вызовов.

Если в теле рекурсивного метода рекурсивный вызов встречается только один раз, значит, что рекурсию можно заменить обычным циклом, что приводит к более эффективной программе, поскольку реализация рекурсии требует временных затрат и работы со стековой памятью.

Приведем традиционный пример рекурсивного определения функции, вычисляющей

Факториал целого числа

// Вычисление факториала в цикле и рекурсивно // n! = 1*2*3*. *(n-1)*n 0!=1 (ро определению) // Поясните, почему правильный результат только для n // Рекурсивная функция static void hanoi(int n, char a, char b, char c ) < if (n < 2) Console.WriteLine(a.ToString() + "->" + c.ToString()); else < hanoi(n - 1, a, c, b); Console.WriteLine(a.ToString() + "->" + c.ToString()); hanoi(n - 1, b, a, c); > > > >

Минимальное число операций равно 2 n -1. Попробуйте придумать более быстрый алгоритм, не изменяя условия задачи. При n=30 мы имеем более 1 миллиарда операций.

А вот практический пример применения рекурсии —

Закрашивание замкнутой области

// Рекурсивное закрашивание using System; namespace Закрашивание < class Program < static void Main() < // Задание границ звездочками 13х16 string[] a =; char[][] b = new char[a.Length][]; // массив b через конструктор // заполнение массива b[][] строками a[] for (int y = 0; y < a.Length; y++) b[y] = a[y].ToCharArray(); print(b); // вывод незакрашенной картинки Console.WriteLine(); // стартовая позиция кисти, попробуй (6,8) и другие . func(b, 3, 8); print(b); // Вывод после закраски Console.ReadKey(); >// Рекурсивное заполнение пробелов символом 'X' static void func(char[][] b, int x, int y) < b[y][x] = 'X'; if (b[y - 1][x] == ' ') func(b, x, y - 1); if (b[y][x + 1] == ' ') func(b, x + 1, y); if (b[y + 1][x] == ' ') func(b, x, y + 1); if (b[y][x - 1] == ' ') func(b, x - 1, y); >// покраска в три цвета static void print(char[][] b) < for (int y = 0; y < b.GetLength(0); y++) < for (int x = 0; x < b[y].Length; x++) < // Console.Write(b[y][x]); if (b[y][x] == ' ') Console.BackgroundColor = ConsoleColor.Green; if (b[y][x] == '*') Console.BackgroundColor = ConsoleColor.Yellow; if (b[y][x] == 'X') Console.BackgroundColor = ConsoleColor.Blue; Console.Write(" "); >Console.WriteLine(); > > > >

Основная идея рекурсии заложена в func(char[][] b, int x, int y): проверка соседних клеток на предмет возможности закрашивания произвольной замкнутой области.

Пример косвенной рекурсии

• Через рекуррентные соотношения, используя цикл, найти C_N и S_N.
• Записать решение, используя косвенную рекурсию.
• Сравнить время выполнения алгоритмов для N = 10, 11, … , 32.

class Program < static double x; static double y; static void Main() < Console.Write("Введите x ( |x| Console.WriteLine("Результат через рекуррентные соотношения: C = , S = .", C, S); DateTime t2 = DateTime.Now; int w = t2.Minute * 60 + t2.Second - t1.Minute * 60 - t1.Second; Console.WriteLine("Время в секундах: " + w); // через рекурсию t1 = DateTime.Now; Console.WriteLine("Результат через косвенную рекурсию: C = , S = .", CR(n), SR(n)); t2 = DateTime.Now; w = t2.Minute * 60 + t2.Second - t1.Minute * 60 - t1.Second; Console.WriteLine("Время в секундах: " + w); Console.ReadKey(); > // косвенная рекурсия static double CR(int n) < double c; if (n >1) c = CR(n - 1) * x - SR(n - 1) * y; else c = x; return c; > static double SR(int n) < double s; if (n >1) s = SR(n - 1) * x + CR(n - 1) * y; else s = y; return s; > >

Отмечу, что в языке логического программирования Prolog конструкции типа цикла могут быть реализованы только через рекурсию.

Завершим раздел рассмотрением двух из трех ключевых принципов ООП — наследования и полиморфизма, считаю принцип инкапсуляции уже достаточно ясным.

NEW: Наш Чат, в котором вы можете обсудить любые вопросы, идеи, поделиться опытом или связаться с администраторами.

Источник