Динамическое программирование на примерах
Динамическое программирование — очень широкое понятие, под которое подходит множество алгоритмов, которым посвящены отдельные лекции. Формально, динамическое программирование — способ решения задач с помощью разбиения их на подзадачи и комбинирования ответов на них. Впрочем, для абсолютного большинства людей, не сталкивавшихся раньше с ДП, это определение ничего не объясняет. Попробуем изменить его так, чтобы оно стало немного понятнее, но всё ещё подходило под большинство примеров из олимпиадного программирования:
Динамическое программирование — способ решения задачи с помощью выражения ответа в виде функции от ответов на ту же задачу для других входных данных.
Скорее всего, всё ещё непонятно. Гораздо эффективнее будет привести несколько примеров, начиная с самого элементарного.
Связь между ДП и рекурсией. Последовательность Фибоначчи
Если вы всё же что-то вынесли из приведённого выше определения, то могли заметить, насколько оно похоже на определение рекурсивной функции. На самом деле, ДП — это “всего лишь” способ решения задач на рекурсивные последовательности с сохранением ответа.
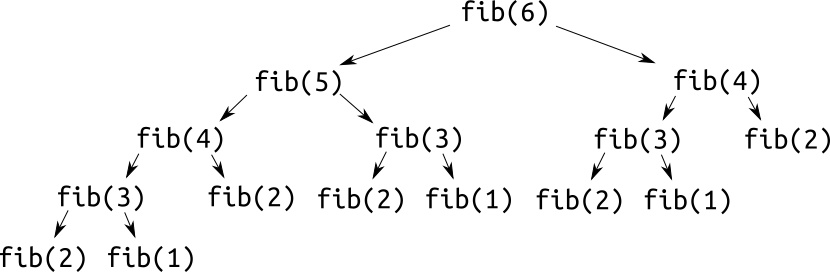
Вспомним реализацию расчёта \(n\)-го числа Фибоначчи из лекции про рекурсию:
Идея проста: для вычисления \(fib(n)\) нам нужны значения \(fib(n — 1)\) и \(fib(n — 2)\). Давайте просто считать \(fib\) в порядке возрастания \(n\), сохраняя результаты в массив.
В большинстве случаев ДП характеризуется тремя главными параметрами:
- Начальные значения. Аналогично крайним случаям в рекурсивных функциях.
- Формула перехода. Описывает рекурсивную зависимость.
- Вычисление ответа. В некоторых случаях ответ может быть не последним значением, а суммой или максимумом по значениям.
Путь в матрице
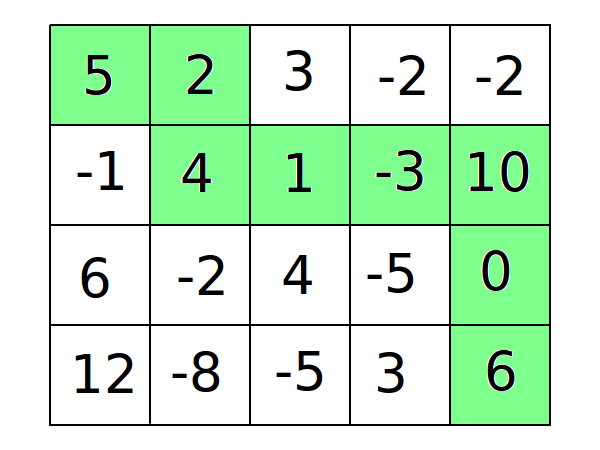
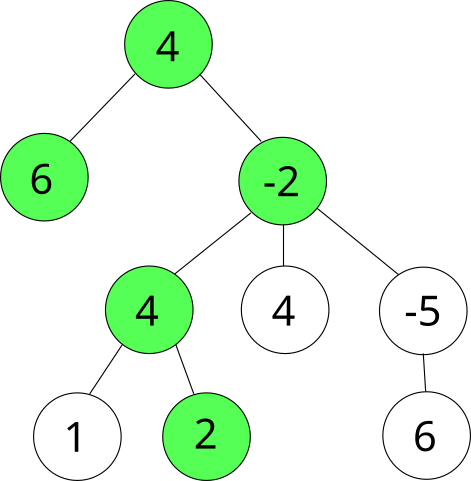
Задачи на поиск оптимального пути в матрице, наверное, самые классические, после задач на последовательность Фибоначчи. В таких задачах каждой клетке в матрице присвоено некоторое число, и нужно найти путь между двумя клетками с максимальной или минимальной суммой.
Приведём решение такой задачи. Будем искать путь между левой верхней и правой нижней клетками с максимальной суммой, если ходить можно только вниз или вправо. Для решения задачи используем следующее ДП: \(dp[i][j]\) — максимальная сумма, которую мы можем набрать, дойдя до клетки \((i, j)\). Опишем ДП:
- Начальные значения: \(dp[0][0] = c[0][0]\) (\(c\) — исходная матрица).
Мы находимся в клетке \((0, 0)\), значит мы ещё не двигались, то есть собранная нами сумма равна значению в этой клетке. - Формула перехода: \(dp[i][j] = \max(dp[i — 1][j], dp[i][j — 1]) + c[i][j]\)
Мы можем перейти в клетку \((i, j)\) либо сверху, либо слева. Выгоднее перейти из той, в которую мы до этого пришли с большей суммой. - Ответ: \(dp[n — 1][m — 1]\).
Как можно заметить, сложность такого решения \(O(N^2)\). Существует другое решение этой задачи, не такое тривиальное, имеющее имеет сложность \(O(N \log N)\). Его можно охарактеризовать как ДП (с натяжкой), но оно значительно отличается от примеров выше. Разберём его.
Будем идти по последовательности слева направо, поддерживая массив \(d\), где \(d[i]\) — минимальный последний элемент среди всех возможных возрастающих подпоследовательностей длиной \(i\). Если таковых не существует, то примем \(d[i] = \infty\). Можно достаточно тривиально доказать, что массив \(d\) будет строго возрастающим:
По определению \(d[i]\) — минимальный последний элемент среди всех подпоследовательностей длиной \(i\). Значит, \(i\)-ый элемент любой подпоследовательности длиной больше \(i\) не меньше, чем \(d[i]\). Следовательно, не может существовать строго возрастающей подпоследовательности длиной \(i + 1\), такой что её последний элемент меньше либо равен \(d[i]\), что и требовалось доказать.
Пусть мы обрабатываем очередной элемент \(a[i]\), и хотим с его помощью продлить некоторые последовательности. С помощью бинарного поиска найдём в массиве \(d\) первый такой индекс \(j\), что \(a[i] < d[j]\). Утверждается, что элемент \(a[j]\). может эффективно продолжить только последовательность длиной \(j - 1\). Доказательство:
Если эта задача показалась вам слишком сложной, не расстраивайтесь. Она приведена в этой лекции в качестве “бонусного” материала. Вернитесь к этой теме через пару месяцев.
brestprog
Олимпиадное программирование в Бресте и Беларуси