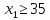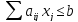Распространенные задачи математического программирования

Формулировка задачи математического программирования

Задачи математического программирования, как правило, содержат большое число переменных и ограничений и не всегда допускают умозрительный анализ. Здесь требуется тщательная формализация и включение в математическую модель всех сколько-нибудь существенных ограничений.

Прежде чем построить математическую модель задачи, необходимо четко разобраться с ситуацией, описанной в условии. Для этого необходимо с точки зрения заданной задачи, а не математики, ответить на следующие вопросы:

1) Что является искомыми величинами задачи?

2) Какова цель решения? Какой параметр задачи служит критерием эффективности (оптимальности) решения, например, прибыль, себестоимость, время и т.д. В каком направлении должно изменяться значение этого параметра (к max или к min) для достижения наилучших результатов?

3) Какие условия в отношении искомых величин и ресурсов задачи должны быть выполнены? Эти условия устанавливают, как должны соотноситься друг с другом различные параметры задачи, например, количество ресурса, затраченного при производстве, и его запас на складе; количество выпускаемой продукции и емкость склада, где она будет храниться; количество выпускаемой продукции и рыночный спрос на эту продукцию и т.д.

После предварительной постановки задачи получают ее формальное решение для простейших случаев, на которых можно проанализировать корректность поставленной задачи. На основании такого анализа вводятся дополнительные параметры и ограничения, проверяется корректность отнесения задачи к тому или иному классу, корректность введения линейности.

Общая схема формализации на основании содержательного описания задачи:

1.Определение переменных задачи (основных параметров).

2. Определение управляющих переменных, характеризующих существо действий и их элементарных составляющих.

3. Формулировка критериев эффективности через параметры и управляющие переменные.

4. Определение ограничений (области допустимых решений) через переменные задачи.

Задача математического программирования содержит n переменных x_i (i=1, 2,. . . , n), образующих n-мерный вектор переменных х.

На переменные накладываются ограничения — в форме равенств h_i(x) = 0, i = 1, . . . , p или неравенств g_i(x) ≥ 0, i = 1, . . . , q.

f(x) – целевая функция (в общем случае нелинейная) всех или некоторых переменных x_i (i=1, 2,. . . , n).

Задача математического программирования формулируется следующим образом:

Минимизировать (или максимизировать) f(x) при условиях g_i(x) ≥ 0, i = 1, . . . , q; h_i(x) = 0, i = 1, . . . , p. Или кратко Min f(x)│ g_i(x) ≥ 0, i = 1, . . . , q; h_i(x) = 0, i = 1, . . . , p>.

6.2 Модели линейного программирования

Линейное программирование применяется при решении задач оптимального распределения ресурсов, управления и планирования производства; определения оптимального размещения оборудования; оптимального плана перевозок груза (транспортная задача) и т.д.

По оценкам американских экспертов около 75% от общего числа применяемых оптимизационных методов приходится на линейное программирование. Около четверти машинного времени, затраченного в последние годы на проведение научных исследований, было отведено решению задач линейного программирования и их многочисленных модификаций.

Задачи линейного программирования относятся к категории оптимизационных. Они находят широкое применение в различных областях практической деятельности: при организации работы транспортных систем, в управлении промышленными предприятиями, при составлении проектов сложных систем. Многие распространенные классы задач системного анализа, в частности, задачи оптимального планирования, распределения различных ресурсов, управления запасами, календарного планирования, межотраслевого баланса укладываются в рамки моделей линейного программирования.

Несмотря на различные области приложения, данные задачи имеют единую постановку: найти значения переменных x₁, …, x_n, доставляющие оптимум заданной линейной формы z=c₁x₁ + c₂x₂+… + c_nx_n при выполнении системы ограничений, представляющих собой также линейные формы.

В задачах линейного программирования критерий эффективности и функции в системе ограничений линейны.

Если содержательный смысл требует получения решения в целых числах, то такая задача является задачей целочисленного программирования.

Если в задаче математического программирования имеется переменная времени, а критерий эффективности выражается через уравнения, описывающие течение операций во времени, то такая задача является задачей динамического программирования.

При описании реальной ситуации с помощью линейной модели следует проверять наличие у модели свойств пропорциональности, аддитивности.

Основные допущения при построении линейных моделей:

-. неотрицательность (не может быть отрицательного объема производства).

Пропорциональность — затраты ресурсов пропорциональны объему производства — вклад каждой переменной в целевой функционал и общий объем потребления соответствующих ресурсов должен быть прямо пропорционален величине этой переменной.

Например, если, продавая j-й товар в общем случае по фиксированной цене, фирма будет делать скидку при определенном уровне закупки до более низкого уровня цены, то будет отсутствовать прямая пропорциональность между доходом фирмы и количеством проданного товара. Т.е. в разных ситуациях одна единица j-го товара будет приносить разный доход.

Аддитивность означает, что целевой функционал и ограничения должны представлять собой сумму вкладов от различных переменных. Величина, соответствующая целому объему всегда равна сумме величин, соответствующих его частям при любом способе разбиения на части.

Примером нарушения аддитивности служит ситуация, когда увеличение сбыта одного из конкурирующих видов продукции, производимых одной фирмой, влияет на объем реализации другого.

Решение практической задачи нельзя считать законченным, если найдено оптимальное решение. Некоторые параметры задачи (финансы, запасы сырья, производственные мощности и др.) можно регулировать, что, в свою очередь, может изменить найденное оптимальное решение. Эта информация получается в результате выполнения анализа чувствительности. Анализ чувствительности позволяет оценить влияние этих параметров на оптимальное решение. Если обнаруживается, что оптимальное решение можно улучшить за счет небольших изменений заданных параметров, то целесообразно реализовать эти изменения.

Источник

1. Определение задачи математического программирования

Математическое программирование — это область математики, разрабатывающая теорию, решения многомерных задач с ограничениями. В отличие от классической математики, мы находим наилучший вариант из всех возможных.

Итак, математическое программирование — это раздел высшей математики, занимающийся решением задач, связанных с нахождением экстремумов функций нескольких переменных при наличии ограничений на переменные.

Общая задача М. п. состоит в нахождении оптимального (максимального или минимального) значения целевой функции, причем значения переменных должны принадлежать некоторой области допустимых значений.

Классическая задача математического программирования – задача выбора таких значений некоторых переменных, подчиненных системе ограничений в форме равенств, при которых достигается max или min функции.

2. Допустимое решение задачи, одр, оптимальное решение задачи.

Допустимым решением задачи называется любой n-мерный вектор

x (x = (,,…,)), удовлетворяющий системе ограничений и условию неотрицательности.

Множество допустимых решений образует ОДР.

Оптимальным решением задачи называется такое допустимое решение, при котором целевая функция достигает экстремума.

3. Экономико–математические модели задач лп: задача о банке

К экономико-математическим моделям задач ЛП относятся:Задача планирования производства, определения оптимального ассортимента продукции, о диете, о банке, составления жидких смесей, Транспортная задача

Построение экономико – математической модели.

Задача о банке

Собственные средства банка в сумме с депозитами составляют 100 млн. $. Не менее 35 млн. $ из этой суммы размещена в кредитах (не ликвид). Ликвидное ограничение ценных бумаг должны составлять не менее 30 %, размещенных в кредитах и ликвидных активах.

Пусть 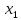— средства, размещенные в кредитах,– средства, размещенные в ликвидных активах.

Банк. Огран. (1)

Кред. Огран.

Ликвид. Огран.

Условие неопределенности ,≥0 (4)

— доходность кредитов, — доходность ликвидных активов

F = при услов. (1) – (4).

4. Экономико – математические модели задач лп: задача определения оптимального ассортимента продукции.

— П1, — П2

F = 3

2

3

5. Задача лп, стандартная форма, каноническая форма.

К математическим задачам линейного программирования относят исследования конкретных производственно-хозяйственных ситуаций, которые в том или ином виде интерпретируются как задачи об оптимальном использовании ограниченных ресурсов.

Задачей линейного программирования является выбор из множества допустимых планов наиболее выгодного (оптимального).

Экономико-математическая модель любой задачи линейного программирования включает: целевую функцию, оптимальное значение которой (максимум или минимум) требуется отыскать; ограничения в виде системы линейных уравнений или неравенств; требование неотрицательности переменных.

В общем виде модель записывается следующим образом:

Целевая функция: F (x)= c1x1 + c2x2 + . + cnxn → max(min)

ограничения: a11x1 + a12x2 + . + a1nxn b1,

требование неотрицательности: xj ≥ 0,

Задача имеет каноническую форму, если является задачей на максимум (минимум) линейной функции F и ее система ограничений состоит только из равенств (уравнений). При этом переменные задачи х1, х2, . хn являются неотрицательными:

F (x) =

, i= 1,2…m

, j = 1,2…n

В стандартной форме задача линейного программирования является задачей на максимум (минимум) линейной функции f и система ограничений ее состоит из одних линейных неравенств типа «

F (x) =

, i= 1,2…m

, j = 1,2…n

Допустимое множество решений задачи ЛП либо пусто, либо является выпуклым многогранником (как пересечение полупространств, описываемых ограничениями-неравенствами). Оно может быть как ограниченным, так и неограниченным; в любом случае это замкнутый многогранник.

Если допустимое множество не пусто, а целевая функция ограничена сверху (для задачи максимизации, а для задачи минимизации — ограничена снизу) на этом множестве, то задача ЛП имеет оптимальное решение.

Оптимальные решения задачи ЛП (если они существуют) всегда находятся на границе допустимого множества. Точнее, если существует единственное оптимальное решение, то им является какая-либо вершина многогранника допустимых решений; если две или несколько вершин являются оптимальными решениями, то любая их выпуклая комбинация также является оптимальным решением (т.е. существует бесконечно много точек максимума или минимума)

Источник