Расчет интеграла в питоне

Дифференцирование и интегрирование функций#

В рамказ компьютерной арифметики предельный переход осуществить невозможно, поэтому в целях аппроксимации производной нередко вместо предела при \(h \to 0\) подставляют очень малое \(h\) :

Такая аппроксимация производной называется правой разностной производной. Можно показать, что асимптотическая погрешность вычисления производной таким способом имеет вид \(o(h)\) , т.е. уменьшая шаг \(h\) можно добиться любой точности вычисления производной. Более распространенна центральная разнастная производная, определяемая выражением

Её асимптотическая погрешность имеет вид \(o(h^2)\) , а значит уменьшая шаг \(h\) в 2 раза, можно ожидать уменьшение погрешности вычисления производной в 4 раза.

Аналогичным образом можно определить аппроксимацию производной любого порядка. Метод scipy.misc.derivative в SciPy вычисляет разностную производную произвольного порядка (опциональный параметр n ).

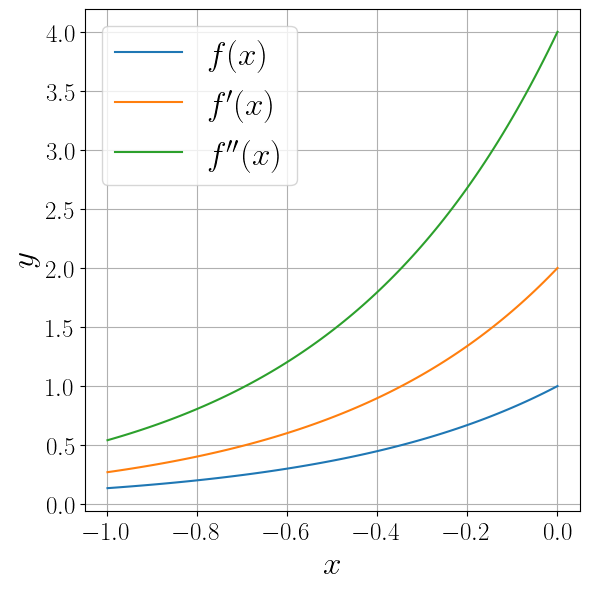
Продемонстрируем его применение на примере функции \(f(x) = e^\) .

from scipy.misc import derivative import numpy as np def f(x): return np.exp(2. * x) fig, ax = plt.subplots(figsize=(6, 6), layout="tight") x = np.linspace(-1, 0, 100) labels = ("$f(x)$", "$f'(x)$", "$f''(x)$") for n, label in enumerate(labels): y = derivative(f, x, n=n, dx=1e-3, order=2*n+1) if order > 0 else f(x) ax.plot(x, y, label=label) ax.set_xlabel("$x$") ax.set_ylabel("$y$") ax.legend() ax.grid() 

Аналитическое дифференцирование#

Ряд современных библиотек умеет вычислять производные от своих методов. Например, библиотека autograd.

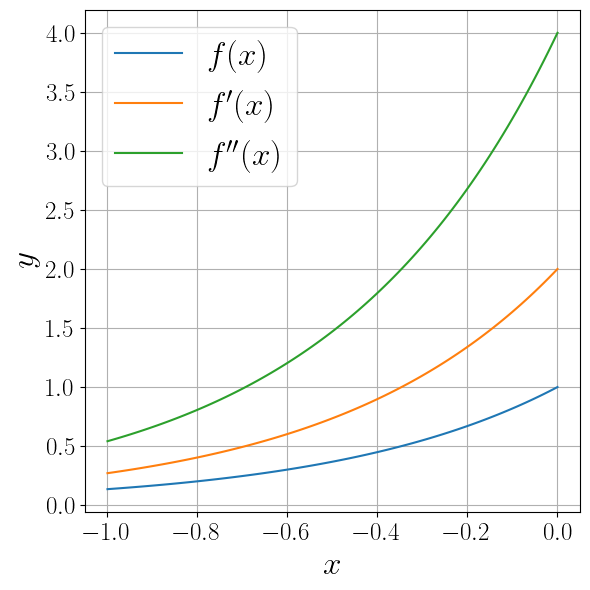
Обратите внимание, что для аналитического вычисления производной средствами библиотеки autograd , необходимо вместо библиотеки NumPy использовать модуль autograd.numpy .

from autograd import numpy as np from autograd import elementwise_grad fig, ax = plt.subplots(figsize=(6, 6), layout="tight") x = np.linspace(-1, 0, 100) labels = ("$f(x)$", "$f'(x)$", "$f''(x)$") funcs = (f, elementwise_grad(f), elementwise_grad(elementwise_grad(f))) for order, (label, func) in enumerate(zip(labels, funcs)): ax.plot(x, func(x), label=label) ax.set_xlabel("$x$") ax.set_ylabel("$y$") ax.legend() ax.grid() 

Интегрирование функций#

Подмодуль scipy.integrate позволяет приближенно вычислять значение определенных интегралов.

Однократные интегралы#

Функция scipy.integrate.quad позволяет проинтегрировать функцию \(f\colon \mathbb \to \mathbb\) . Вызов функции quad(f, a, b) приближенно находит значение интеграла

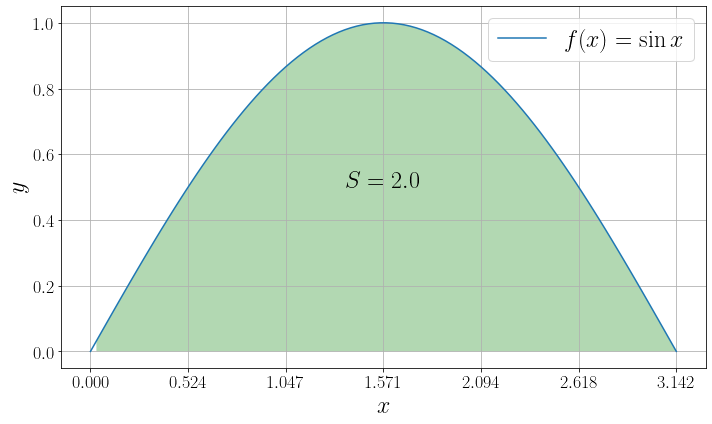
В качестве примера найдем численно значение интеграла

import numpy as np from scipy import integrate from matplotlib import pyplot as plt f = np.sin a, b = 0, np.pi I, _ = integrate.quad(f, 0, np.pi) x = np.linspace(0, np.pi, 100) y = f(x) fig, ax = plt.subplots(figsize=(10, 6), layout="tight") ax.plot(x, y, label=r"$f(x)=\sin x$") ax.set_xlabel("$x$") ax.set_ylabel("$y$") ax.fill_between(x, np.zeros_like(x), y, where=(y>0), facecolor='green', alpha=0.30) ax.set_xticks(np.linspace(0, np.pi, 7)) ax.text(np.pi/2, 0.5, fr"$S = I>$", fontdict="size": 24, "ha": "center">) ax.legend() ax.grid() 

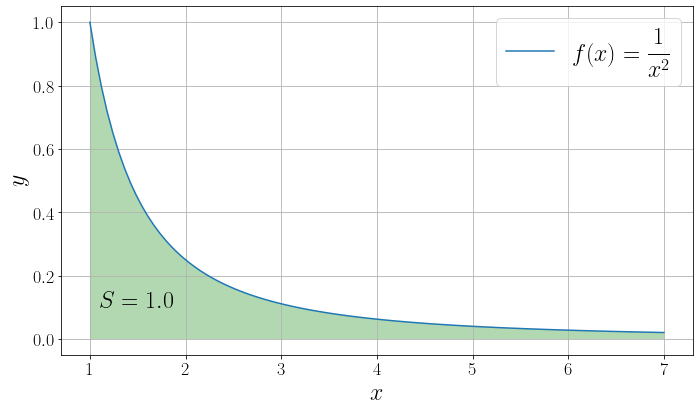
Параметры \(a\) и \(b\) могут принимать значения -inf и +inf , чтобы брать несобственные интегралы. Продемонстрируем это на примере интеграла

def f(x): return 1. / np.square(x) a, b = 1, np.inf I, _ = integrate.quad(f, a, b) x = np.linspace(a, 7, 100) y = f(x) fig, ax = plt.subplots(figsize=(10, 6), layout="tight") ax.plot(x, y, label=r"$f(x)=\dfrac $") ax.set_xlabel("$x$") ax.set_ylabel("$y$") ax.fill_between(x, np.zeros_like(x), y, where=(y>0), facecolor='green', alpha=0.30) ax.set_xticks(np.linspace(1, 7, 7)) ax.text(1.5, 0.1, fr"$S = I>$", fontdict="size": 24, "ha": "center">) ax.legend() ax.grid() 

Однако численное взятие несобственных интегралов отнюдь не тривиальная задача. Например, интеграл Френеля $ \( \int\limits_0^\infty \sin x^2 \, dx = \sqrt<\dfrac<\pi>> \) $

просто так вычислить не удастся.

def f(t): return np.sin(t**2) I, _ = integrate.quad(f, 0, np.inf) print(I) 

C:\Users\fadeev\AppData\Local\Temp/ipykernel_8252/3166585030.py:4: IntegrationWarning: The integral is probably divergent, or slowly convergent. I, _ = integrate.quad(f, 0, np.inf)

Интегралы большей кратности#

Функция scipy.integrate.dblquad позволяет вычислять интегралы вида

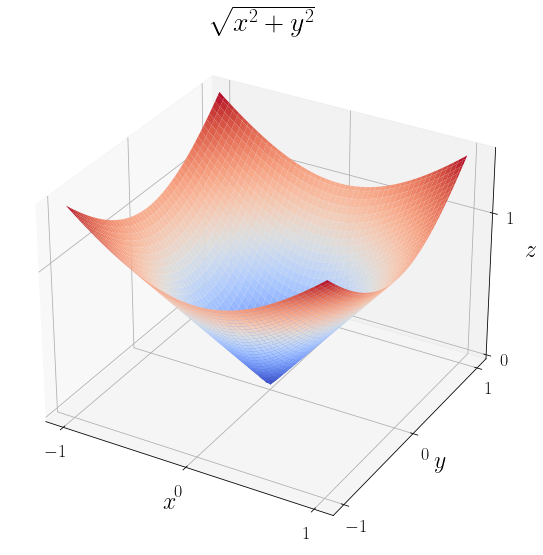
В качестве примера возьмём интеграл функции \(f = \sqrt\) в области \(D\) совпадающей с кругом единичного радиуса с центром в начале:

import numpy as np from scipy import integrate from matplotlib import pyplot as plt def h(x): return np.sqrt(1 - x**2) def g(x): return -h(x) def f(x, y): return np.sqrt(x**2 + y**2) a, b = -1, 1 I, _ = integrate.dblquad(f, -1, 1, g, h) x = np.linspace(a, b, 100) y = np.linspace(a, b, 100) x, y = np.meshgrid(x, y) z = f(x, y) fig, ax = plt.subplots(figsize=(8, 8), layout="tight", subplot_kw="projection": "3d">) ax.plot_surface(x, y, z, cmap="coolwarm") ax.set_xlabel("$x$") ax.set_ylabel("$y$") ax.set_zlabel("$z$") ax.set_xticks([-1, 0, 1]) ax.set_yticks([-1, 0, 1]) ax.set_zticks([0, 1]) ax.set_title(r"$\sqrt$") print(f"Вычисленное значение интеграла: I>, точное значение: 2*np.pi/3>.") 

Вычисленное значение интеграла: 2.0943951023924106, точное значение: 2.0943951023931953.

Трехкратные интегралы вида

можно вычислить методом integrate.tplquad. Интеграл произвольной кратности можно вычислить методом integrate.tplquad.

Источник

Русские Блоги

Вычисление интеграла с помощью модуля Scipy в Python

Метод получения интеграла в модуле Scipy на Python:

SciPy реализует базовое использование функции, чтобы найти интеграл функции, интеграл, продвинутая математика имеет много разговоров, основной смысл — найти площадь под кривой.

Среди них rn можно рассматривать как отклонение, которым обычно можно пренебречь, а wi можно рассматривать как вес.

SciPy предоставляет множество функций для вычисления различных типов интегралов, которые можно разделить на две категории в зависимости от разницы входных параметров: одна — это вход известной функции и верхний и нижний пределы интеграла; другая — набор входных точек.Это применимо к некоторым данным, собранным после физической реализации, но функция не может быть определена, но есть много точек данных, тогда какая площадь под огибающей этих точек также является интегральной проблемой, поэтому существует точка, установленная в функции SciPy Integral, параметр функции — это массив или список в форме.

1. Интеграл с известным типом функции

В этом разделе показано, как вычислить интеграл в SciPy в виде нескольких вопросов.

• Вопрос 1: Здесь предположим, что функция f (x) = x + 1, верхний и нижний пределы интеграла равны [1,2] математическое выражение:

Вы можете использовать подмодуль, интегрированный в модуль Scipyчетырехъядерная функцияНайти расчетное значение этой математической задачи.

from scipy import integrate def f(x): return x + 1 v, err = integrate.quad(f, 1, 2) print v 

Результат выполнения программы:

2.5

Вопрос 2:Но для функции f (x) = ax + b, можно ли использовать функцию quad, если a и b могут быть неизвестны? Ответ - да, quad имеет формальный параметр args, который можно передавать в некоторых параметрах.

from scipy import integrate def f(x, a, b): return a * x + b v, err = integrate.quad(f, 1, 2, args = (-1, 1)) print v 

Результат выполнения программы:

-0.5

Вопрос 3:Если вы встретите точку останова в интегральной функции, вы можете использовать точки функции quad, чтобы задать точку останова и продолжить интегрирование. Например:

Вотf (x) вЕсть точка останова, где x = 0, если точка останова не указана, она будет вычислена путем вычисления квадратов:

from scipy import integrate import numpy as np def f(x): return 1 / np.sqrt(abs(x)) v, err = integrate.quad(f, -1, 1) print v 

scipy1801.py:4: RuntimeWarning: divide by zero encountered in double_scalars return 1 / np.sqrt(abs(x)) inf 

Результат — бесконечность (бесконечность, бесконечность) и есть ошибка деления на 0! немного отредактируйте:

from scipy import integrate import numpy as np def f(x): return 1 / np.sqrt(abs(x)) v, err = integrate.quad(f, -1, 1, points=[0]) print v 

Мы можем нарисовать визуальную кривую этой функции:

from scipy import integrate import numpy as np def f(x): return 1 / np.sqrt(abs(x)) v, err = integrate.quad(f, -1, 1, points=[0]) print v 

import numpy as np, matplotlib.pyplot as plt
from mpl_toolkits.mplot3d.axes3d import Axes3D
fig, ax = plt.subplots(figsize=( 8, 3))
x = np.linspace(- 1, 1, 10000)
ax.plot(x, f(x), lw= 2)
ax.fill_between(x, f(x), color= ‘green’, alpha= 0.5)
ax.set_xlabel( » x x x «, fontsize= 18)
ax.set_ylabel( » f ( x ) f(x) f ( x ) «, fontsize= 18)
ax.set_ylim( 0, 25)
plt.show()

Получите следующую таблицу результатов:

2 Дайте интеграл от множества точек

В случае, если интегральная функция не может быть подтверждена, некоторые последовательности также могут быть интегрированы.

• Вопрос 4： Интегрировать Но есть 10 примеров данных этой функции, функция quad не f (x) = x, но соответствующие (xi,yi)。

from scipy import integrate import numpy as np def f(x): return np.sqrt(x) x = np.linspace(0, 2, 10) y = f(x) v = integrate.trapz(y, x) print v 

3 Несколько точек

Двойной интеграл в SciPy можно вычислить с помощью функции dblquad, а тройной интеграл можно вычислить с помощью функции tplquad. Функцию nquad можно использовать для множественных интегралов от f (x1, x2, . xn).

• Двойная интегральная функция dblquad для вычисления, предположим, что есть функция f (x, y) необходимо вычислить свой двойной интеграл.

Как использовать Scipyфункция dblquadКакая? Общий формат выражения для универсального двойного интеграла:

Тогда первый параметр функции dblquad должен бытьf (x, y), второй, третий, четвертый и пятый - это a, b, g (x), h (x), что означает, что четвертая и пятая функции dblquad являются функцией.

from scipy import integrate import numpy as np def f(x, y): return x * y def h(x): return x v, err = integrate.dblquad(f, 1, 2, lambda x: 1, h) print v 

Результат выполнения программы:

1.125


Тройной интеграл можно вычислить с помощью tplquad. Общий формат выражения тройного интеграла:

tqlquad(f, a, b, g, h, q, r) 

Среди них все функции f, g, h, q и r. Ниже для расчета

Программа, написанная на Python, выглядит так:

from scipy import integrate import numpy as np f = lambda x, y, z : x g = lambda x : 0 h = lambda x : (1 - x) / 2 q = lambda x, y : 0 r = lambda x, y : 1 - x - 2 * y v, err = integrate.tplquad(f, 0, 1, g, h, q, r) print v 

Результаты выполнения программы:

0.02083333333

Источник