- Использование функций scipy.stats. Доверительные интервалы.
- Оценка математического ожидания нормального распределения при известном \(\sigma\)
- Оценка математического ожидания нормального распределения при неизвестном \(\sigma\)
- Список использованных источников
- Как рассчитать доверительный интервал как в R, так и в Python
Использование функций scipy.stats. Доверительные интервалы.
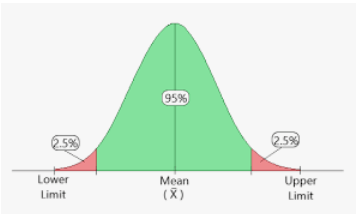
В математической статистике интервальной оценкой называется результат использования выборки для вычисления интервала возможных значений неизвестного параметра, оценку которого нужно построить. Следует отличать от точечной оценки, которая даёт лишь одно значение. Самым распространенным видом интервальных оценок являются доверительные интервалы.
Доверительная вероятность — вероятность того, что доверительный интервал накроет неизвестное истинное значение параметра, оцениваемого по выборочным данным.
Оценка математического ожидания нормального распределения при известном \(\sigma\)
Количественный признак генеральной совокупности X распределен нормально и известно среднеквадратическое отклонение этого распределения. Из генеральной совокупности формируется выборка, по которой определяется математическое ожидание выборки \(\hat\).
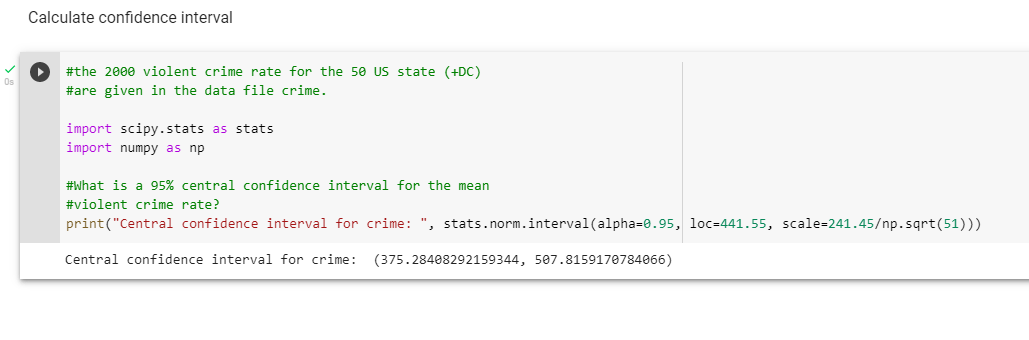
Необходимо найти доверительный интервал \([\hat-d, \hat+d]\), который покрывает неизвестное математическое ожидание \(a\) генеральной совокупности с надежностью или доверительной вероятностью \(\gamma\): \(P(|\hat-a| Математическое ожидание выборки \(\hat\) рассматривается как нормально-распределенная случайная величина с математическим ожиданием \(\hat\) и стандартным отклонением \(\sigma/\sqrt\). Если стандартное отклонение генеральной совокупности неизвестно, то для определения доверительного интервала используется распределение Стьюдента: \[P(\hat-t_\gamma s/\sqrt < a < \hat+t_\gamma s/\sqrt) = 2 \int_^ где \(s\) — “исправленное” среднеквадратичное отклонение выборки, \(S(t,n)\) — плотность распределения Стьюдента. При больших выборках (n>30) распределение Стьюдента стремится к нормальному и для оценки доверительного интервала может использоваться нормальное распределение. При малых выборках нормальное распределение будет давать более узкий (т.е. слишком оптимистичный) интервал, в отличие от распределения Стьюдента. В статистике частот доверительный интервал (CI) — это диапазон оценок для неизвестного параметра. CI вычисляется как заданный уровень достоверности, при чем наиболее распространенным является уровень достоверности 95%. Факторы, влияющие на ширину CI, включают уровень достоверности, размер выборки и вариабельность выборки. При неизменности всех остальных факторов большая выборка привела бы к более узкому CI, большая вариабельность в выборке приводит к более широкому CI, а более высокий уровень достоверности потребовал бы более широкого CI. Ниже приведем формулу доверительного интервала: где, CI — доверительный интервал, x — выборочное среднее значение, z — значение уровня достоверности, s — стандартное отклонение выборки, Намерения данного поста рассчитать доверительный интервал как в R, так и в Python. Был написан код R в Replit, бесплатном онлайн-интерпретаторе/компиляторе. Код Python был переведен с помощью Google Colab, который представляет собой бесплатный онлайн-блокнот Jupyter, размещенный Google. Постановка задачи для этого вопроса такова: Уровень насильственных преступлений за 2000 год по 50 штатам США (+округ Колумбия) приведен в файле данных по преступлениям. Каков 95%-ный центральный доверительный интервал для среднего уровня насильственных преступлений? На этот вопрос был дан ответ с использованием функции qnorm от R, где указаны верхний и нижний диапазоны доверительного интервала. Это приводит к нижнему и верхнему диапазонам CI, составляющим 375,2841 и 507,8159 соответственно: Библиотека scipy.stats на самом деле имеет функцию для вычисления доверительного интервала, который можно увидеть ниже:- Подводя итог, поскольку в библиотеке scipy в Python есть функция, которая конкретно работает с доверительными интервалами, я чувствую, что в данном случае с языком легче работать. Сильно удивляет, что R не создал такую функцию в своем языке программирования.# Стандартное отклонение генеральной совокупности sigma = 0.8 # Математическое ожидание генеральной совокупности mean = 4.1 # Формируем выборку из генеральной совокупности # Объем выборки n = 30 # Выборка data = np.random.normal(loc=mean, scale=sigma, size=n) # Надежность оценки (доверительная вероятность) gamma = 0.95 # Оценка математического ожидания выборки mean_of_sample = np.mean(data) # Стандартное отклонение выборочной средней sigma_of_mean = scipy.stats.sem(data)
interval = scipy.stats.norm.interval(gamma, loc = mean_of_sample, scale = sigma_of_mean) print('Математическое ожидание принадлежит интервалу [; ]'.format(interval[0],interval[1])) Математическое ожидание принадлежит интервалу [3.89; 4.47] Оценка математического ожидания нормального распределения при неизвестном \(\sigma\)
# Надежность оценки gamma = 0.95 # Оценка математического ожидания mean_of_sample = np.mean(data) # Стандартное отклонение выборочной средней совокупности sigma_of_mean = scipy.stats.sem(data)
# Доверительный интервал математического ожидания interval = scipy.stats.t.interval(gamma, df = n-1, loc = mean_of_sample, scale = sigma_of_mean) print(interval) (3.8810695725888413, 4.482390285924866) # Очень маленькая выборка n = 5 data = np.random.normal(loc=mean, scale=sigma, size=n) # Оценка математического ожидания mean_of_sample = np.mean(data) # Стандартное отклонение выборочной средней совокупности sigma_of_mean = scipy.stats.sem(data) # Доверительный интервал математического ожидания с использованием распределения Стьюдента interval = scipy.stats.t.interval(gamma, df = n-1, loc = mean_of_sample, scale = sigma_of_mean) print('Интервал по распределению Стьюдента [; ]'.format(interval[0],interval[1])) # Доверительный интервал математического ожидания с использованием нормального распределения interval = scipy.stats.norm.interval(gamma, loc = mean_of_sample, scale = sigma_of_mean) print('Интервал по нормальному распределению [; ]'.format(interval[0],interval[1])) Интервал по распределению Стьюдента [3.000; 4.419] Интервал по нормальному распределению [3.209; 4.210] Список использованных источников
Как рассчитать доверительный интервал как в R, так и в Python