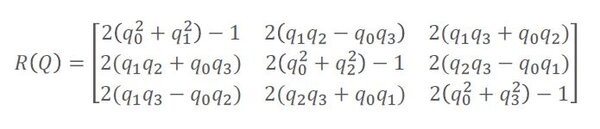Quaternion to rotation matrix python

Introduction

Quaternion and numpy-quaternion seem to be the top two libraries in the world that handle quaternions in Python, but probably because the person who made the reference page for pyquaternion was the first in Japan, the quaternion calculation in Python is overflowing in the streets. It’s just pyquaternion (is there only?).

However, numpy-quaternion seems to have a lower calculation cost. Reference: https://www.theoj.org/joss-papers/joss.00787/10.21105.joss.00787.pdf

Also, comparing the number of stars on github, there are more numpy-quaternions (as of December 13, 2019, numpy-quaternion is 276 and pyquaternion is 138).

I feel that the affinity with numpy is also better than pyquaternion because of the ease of handling batch conversion. Would you like to use it?

github repository: https://github.com/moble/quaternion Documentation: https://quaternion.readthedocs.io/en/latest/ PyPI: https://pypi.org/project/numpy-quaternion/

Installation

pip install numpy-quaternion 

You can easily enter with.

You can import the library with.

Quaternion notation

quat = (w, x, y, z) = \left(\underbrace>_,\ \underbrace<\lambda_x\sin\frac,\ \lambda_y\sin\frac,\ \lambda_z\sin\frac>_\right) 

How to use

import numpy as np import quaternion 

Make a quaternion

quat = np.quaternion(w, x, y, z) 

Quaternion is added to the attribute of numpy. For example

print(np.quaternion(1,0,0,0)) # -> quaternion(1, 0, 0, 0) type(np.quaternion(1,0,0,0)) # -> quaternion.quaternion 

Quaternion synthesis

q1 = np.quaternion(1, 2, 3, 4) q2 = np.quaternion(4, 5, 6, 7) print(q1*q2) # -> quaternion(-52, 10, 24, 20) 

Multiplication is defined. For the time being, other four arithmetic operations are also defined, but do you sometimes use sums . It is not defined in Eigen of C ++.

methods of np.quaternion

Only a part will be taken up. It does not cover things related to spherical functions or linear interpolation. Reference: https://quaternion.readthedocs.io/en/latest/_autosummary/quaternion.html

Member variables

Member variables	function
w	Elements of the real part
x	The first element of the imaginary part
y	The second element of the imaginary part
z	The third element of the imaginary part
components	(w,x,y,z)Is numpy.Returned as an array
imag	Imaginary part(x,y,z)Is numpy.Returned as an array
vec	Imaginary part(x,y,z)Is numpy.Returned as an array
real	Real part(w)Is returned

Member function

Member function	function
abs()	Absolute value of quaternion (Euclidean distance)
absolute()	Absolute value of quaternion
angle()	rotation angle
conj()	Returns the complex conjugate of the quaternion
conjugate()	Returns the complex conjugate of the quaternion
equal(quat)	Is it equal to the quaternion in the argument content?
exp	Returns exponential ( e^q ）
inverse()	Returns a reverse quaternion
isfinite()	Are all elements finite
ininf()	Is there even one inf element?
innan()	Is there even one nan element?
log()	Returns quaternion logs
nonzero()	Are all elements 0
norm()	Quaternion Cayley norm (absolute squared route)
normalized()	Returns a normalized quaternion
notequal(quat)	Is it not equal to the quaternion in the argument content?
sqrt()	Quaternion square-root( quat=q*q Meet q )return it
square()	Quaternion squared (quat*quat) return it

quaternion method

The point is that the methods in this area are not one-dimensional, but can also be used for multidimensional arrays. If the size of the last dimension requires a quaternion, it should be 4, if it is 3D, it should be 3D, and if it is 3×3, the last 2D should be 3×3.

Member function	function
quaternion.as_quat_array(a)	numpy.Convert array to quaternion. The size of the last dimension of a must be 4
quaternion.as_float_array(a)	numpy.quaternion numpy.Convert to array. The dimension of the output is one larger than the input.
quaternion.from_float_array(a)	as_quat_Same as array
quaternion.as_rotation_matrix(q)	numpy.Convert quaternion to 3×3 rotation matrix.
quaternion.from_rotation_matrix(rot, nonorthogonal=True)	Numpy a 3×3 rotation matrix.Convert to quaternion
quaternion.as_rotation_vector(q)	Find the axis of rotation from the quaternion. The magnitude of the last dimension of the output is 3.
quaternion.from_rotation_vector(rot)	Convert from a size 3 rotation axis to a quaternion.
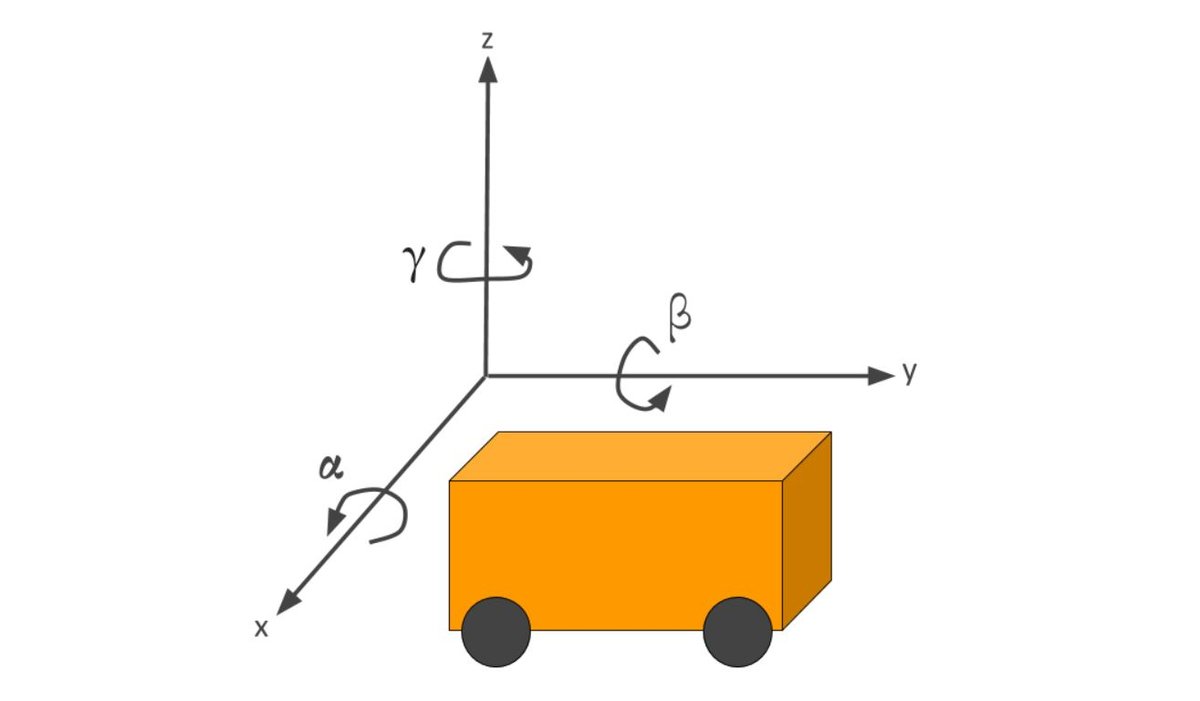
quaternion.as_euler_angles(q)	Convert from quaternion to Euler angles. Refer to the document for the conversion order of Euler angles.
quaternion.from_euler_angles(alpha_beta_gamma, beta=None, gamma=None)	Convert Euler angles to quaternions. Refer to the document for the conversion order of Euler angles.
quaternion.rotate_vectors(R, v, axis=-1)	R is a quaternion and v is a vector. Rotate the vector according to the quaternion.
quaternion.allclose(a, b, rtol=8.881784197001252e-16, atol=0.0, equal_nan=False, verbose=False)	Compare two quaternions
quaternion.integrate_angular_velocity(Omega, t0, t1, R0=None, tolerance=1e-12)	Rotate according to the angular velocity

Official documentation

By the way, the author of this library seems to have a big Euler angle. Stop if you see someone using it! Say that and walk away from the spot and mess with your mom! Is written

Finally

Where is the demand for quaternions in Python? Unity is C #, and I’m talking about using Unity’s functions in the first place, and Python is too slow for robots, which is out of the question .

Источник

What is a Quaternion?

A quaternion is one of several mathematical ways to represent the orientation and rotation of an object in three dimensions. Another way is to use Euler angle-based rotation matrices like I did on this post and this post (i.e. roll, pitch, and yaw), as well as the cover image of this tutorial.

Quaternions are often used instead of Euler angle rotation matrices because “compared to rotation matrices they are more compact, more numerically stable, and more efficient” (Source: Wikipedia).

Note that a quaternion describes just the rotation of a coordinate frame (i.e. some object in 3D space) about an arbitrary axis, but it doesn’t tell you anything about that object’s position.

The Use of Quaternions in Robotics

Quaternions are the default method of representing orientations and rotations in ROS, the most popular platform for robotics software development.

In robotics, we are always trying to rotate stuff. For example, we might observe an object in a camera. In order to get a robotic arm to grab the object, we need to rotate the camera reference frame to the robot reference frame so that the robot “knows” the location of the object in its own coordinate frame.

Once the rotation from camera pixel coordinates to robot base frame coordinates is complete, the robotic arm can then move its motors to the appropriate angles to pick up the object.

How to Represent Quaternions

Quaternions are an extension of complex numbers. However instead of two values (e.g. a + bi or x + yi…same thing) that represent a point (or vector), we have four values (a, b, c, d):

q = a + bi + cj + dk

The four values in a quaternion consist of one scalar and a 3-element unit vector.

Instead of a, b, c, and d, you will commonly see:

q = w + xi + yj + zk or q = q₀ + q₁i + q₂j + q₃k

• q₀ is a scalar value that represents an angle of rotation
• q₁, q₂, and q₃ correspond to an axis of rotation about which the angle of rotation is performed.

Other ways you can write a quaternion are as follows:

The cool thing about quaternions is they work just like complex numbers. In two dimensions, you can rotate a vector using complex number multiplication. You can do the same with quaternions. The math is more complicated with four terms instead of two, but the principle is the same.

Let’s take a look at a two-dimensional example of complex number multiplication so that you can understand the concept of multiplying imaginary (complex) numbers to rotate a vector. Quaternions add a couple more variables to extend this concept to represent rotation in the 3D space.

2D Example

Suppose we have a vector on a 2D plane with the following specifications: (x = 3, y = 1).

This vector can be represented in complex numbers as:

3 + i (e.g. using the x +yi form of complex numbers)

Let’s rotate this vector 45 degrees (which is π/4 in radians).

To rotate 45 degrees, we multiply the number by:

So, we have sqrt means (“take the square root of”):

(1/sqrt(2)+ i/sqrt(2)) * (3 + i) = sqrt(2) + 2sqrt(2)i

(x = 1.414, y = 4.242)

As I mentioned earlier, the math for multiplying real quaternions together is more complex than this, but the principle is the same. Multiply an orientation (represented as a quaternion) by a rotation (represented as a quaternion) to get the new orientation.

Convert a Quaternion to a Rotation Matrix

Given a quaternion, you can find the corresponding three dimensional rotation matrix using the following formula.

Python Code

import numpy as np def quaternion_rotation_matrix(Q): """ Covert a quaternion into a full three-dimensional rotation matrix. Input :param Q: A 4 element array representing the quaternion (q0,q1,q2,q3) Output :return: A 3x3 element matrix representing the full 3D rotation matrix. This rotation matrix converts a point in the local reference frame to a point in the global reference frame. """ # Extract the values from Q q0 = Q[0] q1 = Q[1] q2 = Q[2] q3 = Q[3] # First row of the rotation matrix r00 = 2 * (q0 * q0 + q1 * q1) - 1 r01 = 2 * (q1 * q2 - q0 * q3) r02 = 2 * (q1 * q3 + q0 * q2) # Second row of the rotation matrix r10 = 2 * (q1 * q2 + q0 * q3) r11 = 2 * (q0 * q0 + q2 * q2) - 1 r12 = 2 * (q2 * q3 - q0 * q1) # Third row of the rotation matrix r20 = 2 * (q1 * q3 - q0 * q2) r21 = 2 * (q2 * q3 + q0 * q1) r22 = 2 * (q0 * q0 + q3 * q3) - 1 # 3x3 rotation matrix rot_matrix = np.array([[r00, r01, r02], [r10, r11, r12], [r20, r21, r22]]) return rot_matrix

Recent Posts

Connect With Me on LinkedIn!

Welcome to AutomaticAddison.com, the largest robotics education blog online (~50,000 unique visitors per month)!

My goal is to meet everyone in the world who loves robotics. Connect with me on LinkedIn if you found my information useful to you. Also follow my LinkedIn page where I post cool robotics-related content. Don’t be shy! I’d love to hear from you!

Источник