Z3 API in Python
Z3 is a high performance theorem prover developed at Microsoft Research. Z3 is used in many applications such as: software/hardware verification and testing, constraint solving, analysis of hybrid systems, security, biology (in silico analysis), and geometrical problems.
This tutorial demonstrates the main capabilities of Z3Py: the Z3 API in Python. No Python background is needed to read this tutorial. However, it is useful to learn Python (a fun language!) at some point, and there are many excellent free resources for doing so (Python Tutorial).
The Z3 distribution also contains the C, .Net and OCaml APIs. The source code of Z3Py is available in the Z3 distribution, feel free to modify it to meet your needs. The source code also demonstrates how to use new features in Z3 4.0. Other cool front-ends for Z3 include Scala^Z3 and SBV.
Please send feedback, comments and/or corrections to leonardo@microsoft.com. Your comments are very valuable.
Getting Started
Let us start with the following simple example:
x = Int('x') y = Int('y') solve(x > 2, y 10, x + 2*y == 7)
Взламываем crackme при помощи Microsoft Z3Py
Недавно Microsoft опубликовала свой SMT-решатель Z3. Давай попробуем разобраться, как можно применить этот инструмент в практических целях.
Intro
Сначала определимся с терминами и областью применения. SMT — это теоремы специального вида, решаемые в конечных полях. Поскольку вся булева арифметика, используемая в компьютерах, является арифметикой в конечном поле, SMT хорошо подходит для описания программ. При помощи таких теорем можно представить задачу crackme или условия, при которых реализуется уязвимость в ПО.
До публикации использовать Z3 было довольно неудобно. Приходилось учить новый язык, а запустить решатель можно было только на сайте (кстати, там же находится tutorial для тех, кто хочет выучить сам язык). Сейчас Z3 можно запустить на своем компьютере, и к нему теперь доступны различные API (C, C++, .NET, Java, Python), из которых мы будем использовать Z3Py — API для Python.
Устанавливаем Z3
Начнем с установки. Любителям винды придется скачать Z3 с сайта, установить и добавить поддиректорию z3/bin в переменные среды PATH и PYTHONPATH. Линуксоидам нужно выполнить следующие команды:
mkdir z3 cd z3 git clone https://github.com/Z3Prover/z3 cd z3 python scripts/mk_make.py cd build make sudo make installЛокальную документацию генерируем так:
sudo apt-get install doxygen cd doc python mk_api_doc.pyДокументацию можно просмотреть, открыв файл doc/api/html/index.html.
Проверим, все ли правильно установилось. Создаем файл z3example.py cо следующим кодом:
from z3 import * def Check(): a = BitVec('a',32) b = BitVecVal(0xdeaddead,32) c = BitVecVal(0xbeefbeef,32) s=Solver() s.add(LShR(b,2)^a==c) if s.check()==sat: print "Equation satisfiable" print "0x%8X"%s.model()[a].as_long() return print "Equation unsatisfiable" if __name__=="__main__": Check()Осваиваем Z3
Если все установилось правильно, то программа должна вывести:
Equation satisfiable 0x8944C944Что делает этот код? Сначала мы создаем переменную а размером 32 бита, значение которой мы хотим найти. Далее мы создаем две константы соответствующего размера. Потом мы инициализируем решатель. При помощи метода add добавляем в решатель правило: (b>>2)^a=c. Метод check запускает решатель и возвращает значение sat в случае, если решение найдено. Метод model возвращает модель со значениями, удовлетворяющими условию. Модель представляет собой хеш-таблицу, из которой можно получить значение каждой переменной, переданной в решатель.
Z3 поддерживает типы Bool, Int, BitVec, Array, Real, FP (floating point). Типы Bool, Real и Int соответствуют своим названиям. Тип BitVec — это по сути беззнаковое число с определяемым в битах размером. Тип Array позволяет определить типы индексатора и элементов, FP — задать количество битов под экспоненту и мантиссу.
a = Bool('a') b=Int('b') c=Real('c') d=BitVec('d',32) e=Array('e',IntSort(),BoolSort()) f=FP('f',FPSort(8,24))Что такое Sort? Так в Z3 называется тип. Очевидно, IntSort() возвращает тип Int, BoolSort() тип Bool и так далее. Узнать тип переменной можно при помощи метода sort. Например:
python >>> from z3 import * >>> a= Int('a') >>> b= Real('b') >>> (a+b).sort() RealДля типа FP существуют наследственные типы с определенными размерами (Float16/FloatHalf, Float32/FloatSingle, Float64, Float128).
Все типы, кроме Array, можно определять сразу для нескольких переменных. Достаточно добавить к методу суффикс s:
Для всех типов, кроме Array, можно создавать константы. Чтобы инициализировать константу, достаточно добавить к имени типа слово Val и передать ей необходимое значение в качестве первого аргумента. Например:
Для всех типов, кроме BitVec и Array, можно использовать константы без инициализации:
Константы типа Real можно инициализировать рациональными числами. При этом дробное представление сохранится.
Z3 также позволяет создавать функции.
>>> from z3 import * >>> f = Function('f', IntSort(), IntSort(), BoolSort()) >>> a=Int('a') >>> b=Int('b') >>> s=Solver() >>> s.add(ForAll([a,b],f(a,b)==(a==b))) >>> x=Int('x') >>> y=IntVal(0x10) >>> s.add(f(x,y)==BoolVal(True)) >>> if s.check()==sat: . print s.model()[x] . 16Метод ForAll позволяет определить значение функции для всех возможных значений аргумента. Функцию можно определить для отдельных аргументов, тогда Z3 попробует определить функцию для всех значений:
>>> from z3 import * >>> f=Function('f',IntSort(),IntSort(),BoolSort()) >>> s=Solver() >>> s.add(f(0,1)==False) >>> s.add(f(1,1)==True,f(1,0)==False,f(0,0)==True) >>> if s.check()==sat: . print s.model()[f] . [(0, 1) -> False, (1, 1) -> True, (1, 0) -> False, (0, 0) -> True, else -> False]Для повторения логики программы лучше всего использовать тип BitVec, при помощи которого удобно эмулировать операции с регистрами. Он поддерживает битовые сдвиги, вращение, операции и , или и исключающее или . У него есть одна особенность, из-за которой программа может не найти решение твоей проблемы. Операция >> определена в Z3Py не как логический сдвиг, а как арифметический, то есть с переносом значения флага carry в верхний разряд. Для логического сдвига нужно использовать метод LShR. Для операций битового вращения (rol, ror) есть методы RotateLeft и RotateRight.
Напишем простую программу с этими операциями:
from z3 import * def Check(): a,b,c =BitVecs('a b c',32) s=Solver() s.add(RotateLeft(a^b,48)==(RotateRight(c,8)&BitVecVal(0x3457ac24,32))) s.add(a&b&c!=BitVecVal(0,32)) if s.check()==sat: m=s.model() print '0x%0.8X'%m[a].as_long() print '0x%0.8X'%m[b].as_long() print '0x%0.8X'%m[c].as_long() if __name__=='__main__': Check()Тип BitVec можно представить в качестве знакового или беззнакового числа при помощи методов as_signed_long и as_long соответственно. Если нужно перевести тип BitVec в Int внутри решателя, поможет процедура BV2Int. Кстати, в нашем коде использовалась процедура RotateLeft со вторым аргументом 48 при размере вектора 32. Очевидно, его можно упростить. Решатель Z3 делает это автоматически, но можно упростить код и самому при помощи процедуры simplify:
>>>from z3 import * >>> a,b = Ints('a b') >>>simplify((a+1)*(b+3),som=True) 3 +3*a + b + a*bsom — это опция, раскладывающая сложные произведения в сумму. Чтобы просмотреть все параметры функции simplify, необходимо вызвать функцию help_simplify().
Z3 позволяет использовать методы питона в качестве уравнений, что очень удобно, если код, который ты попытаешься представить при помощи SMT, использует циклы. Функция должна возвращать True, False или тип Z3 Bool. На вход ей должны быть переданы только аргументы типов Z3. Например:
from z3 import * def f1(a): b=0x12345678 c=0x23874816 d=0x42146789 return (a^b)==(c^d) def c1(a): b=0x1 i=0 while ipython z3MethodExample.py Satisfiable [b = 1940355559, c = 19403555529, a = 46]Ломаем тестовый кракми
При решении crackme удобно использовать сразу несколько функций. Например, в одной реализовать проверку на символы английского алфавита, а в другой логику самого crackme. Допустим, у нас есть такой crackme:
import sys def Check(a): sm=0 xr=0 for i in a: sm+=ord(i) xr^=ord(i) if ((sm==0x704)and(xr==0x36)): print 'Serial is valid' else: print 'Serial is not valid' if __name__=="__main__": if len(sys.argv)>1: Check(sys.argv[1]) else: print 'Input serial as an argument'Теперь пишем для него решение:
from z3 import * let_list=[] def alphaNumeric(a): return Or(And(a>0x29,a<0x3a),And(a>0x40,a<0x5b),And(a>0x60,a<0x7b)) def Check(length): i=0 while i'.format(i)]=BitVec('l_<>'.format(i),8) let_list.append(globals()['l_<>'.format(i)]) i=i+1 s=Solver() i=0 while i >>> python z3SolveEasyCrackme.py Serial: mozzWzzygztkhpll >>> python easycrackme.py mozzWzzygztkhpll Serial is validЛомаем настоящий кракми
В качестве практики применим Z3 к настоящему ZeroNights Crackme 2013. Скачать его можно по ссылке.
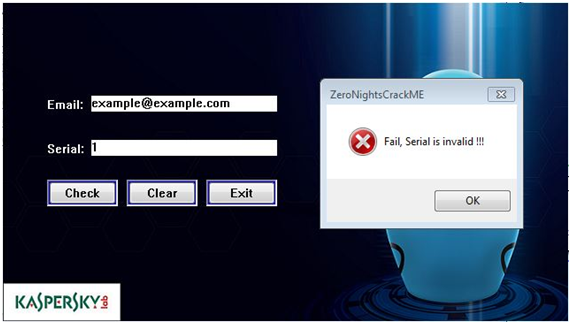
Запускаем приложение, вводим почту и пароль.
- Открываем IDA, запускаем поиск по тексту Fail.
Xakep #207. Дистанционное банковское ограбление
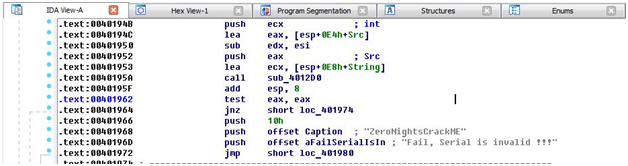
- Изучаем функцию. Это функция обработки всех событий приложения. Нам нужна только ветка проверки серийника.
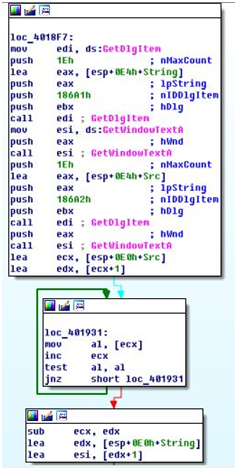
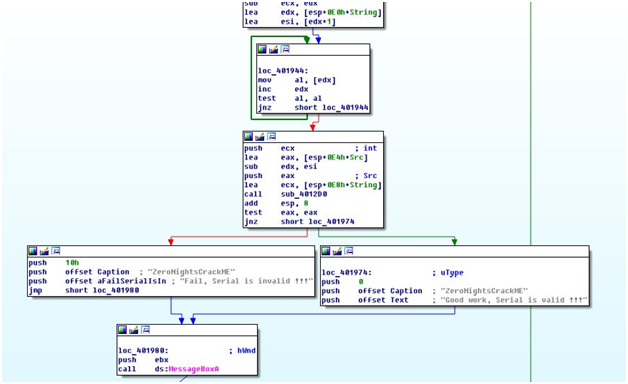
Видно, что процедура берет текст из текстбоксов, высчитывает длины строк и передает сами строки и их размеры в функцию sub_4012D0, в зависимости от результата которой приложение выдает месседжбокс с разным текстом. Посмотрим, что происходит в этой функции.
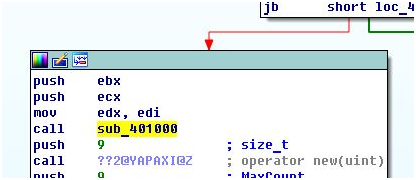
В начале функции мы видим проверку размера одной из строк. Она должна иметь длину 18. Значит, это наш пароль. После этого пароль проверяется на символы цифр и латинского алфавита. Дальше мы видим, что почта передается в функцию sub_401000.
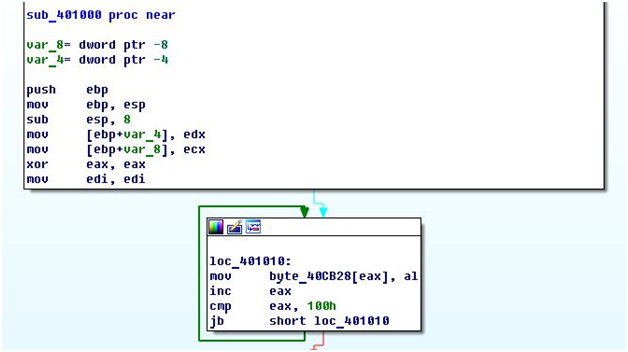
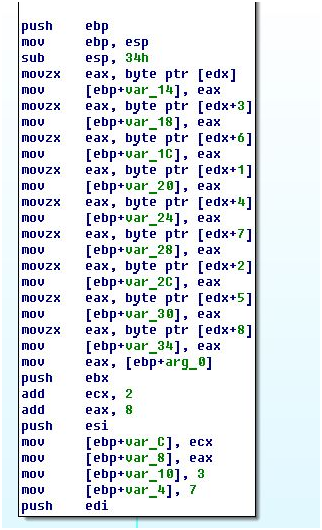
В этой функции производится заполнение массива из 256 байт значениями от 0 до 255.
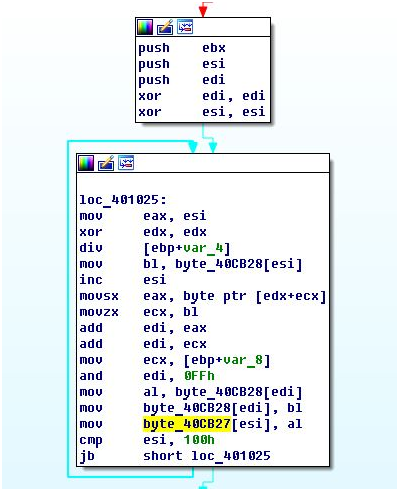
Далее массив перемешивается при помощи почты. Есть два счетчика, инициализированных нулями перед циклом. Первый проходит по значениям от 0 до 255. Ко второму при каждой итерации прибавляется байт из замешиваемого массива по смещению первого счетчика и прибавляется байт почты со смещением на первый счетчик по модулю длины почты. Потом элементы массива на номерах счетчиков меняются местами. Значит, почта применяется для генерации sbox-массива.
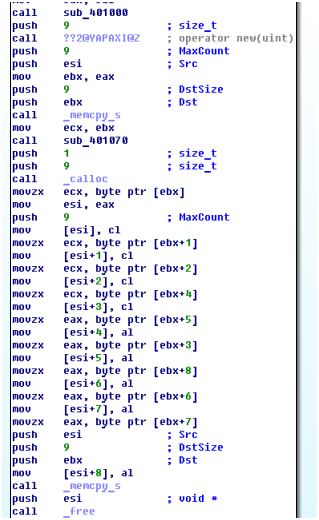
Вернемся в метод sub_4012D0. Мы видим инструкции, повторяемые для двух частей пароля.
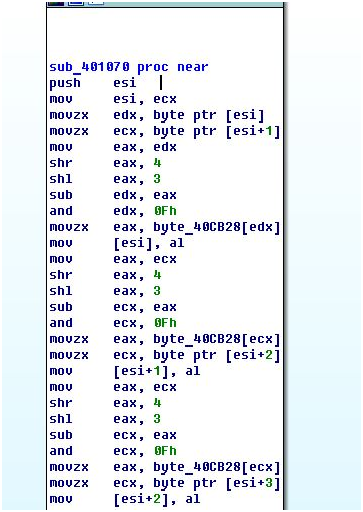
Функция sub_401070 производит манипуляции над каждым символом пароля по следующей формуле:
После этого каждая из обновленных частей копируется в соответствующий новый массив, но со смещением в тройках, то есть:
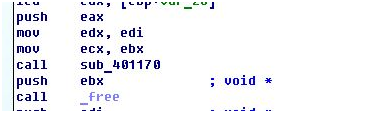
b[0]=a[0]; b[1]=a[1]; b[2]=a[2]; b[3]=a[5]; b[4]=a[3]; b[5]=a[4]; b[6]=a[8]; b[7]=a[6]; b[8]=a[7];После этих манипуляций происходит вызов функции sub_401170 и освобождение лишних массивов.
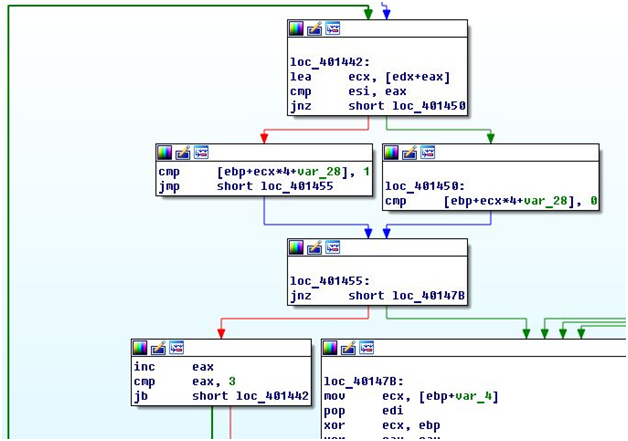
В этой функции происходит копирование второй части пароля в локальный массив и цикл с множеством операций. После анализа цикла оказалось, что он представляет собой перемножение двух квадратных матриц три на три по модулю семь. А то странное копирование со смещением — это сдвиг строки влево на ее номер.
Возвращаемся в предыдущую функцию. Теперь ясно, что следующие действия — это сравнение результата с единичной матрицей.
Результат
Пишем решение crackme на Z3Py:
#!/usr/bin/env python # -*- coding: utf-8 -*- import sys from z3 import * def Find(email): i=0; l=[] while i=BitVecVal(0x30,8), passw[i]<=BitVecVal(0x39,8)), And(passw[i]>=BitVecVal(0x41,8), passw[i]<=BitVecVal(0x5a,8)), And(passw[i]>=BitVecVal(0x61,8), passw[i]<=BitVecVal(0x7a,8)))==True) i=i+1 i=0 while i<9: s.add(sbox[(passw[i]-(LShR(passw[i],4)<<3))&BitVecVal(0xf,8)]==matrix1bsl[i]) s.add(sbox[(passw[i+9]-(LShR(passw[i+9],4)<<3))&BitVecVal(0xf,8)]==matrix2bsl[i]) if (i/3)==(i%3): s.add(result[i]==BitVecVal(1,0x8)) else: s.add(result[i]==BitVecVal(0,0x8)) i=i+1 i=0 while i<3: j=0 while j<3: s.add(matrix1[i*3+j]==matrix1bsl[i*3 +((j+i)%3)]) s.add(matrix2[i*3+j]==matrix2bsl[i*3 +((j+i)%3)]) j=j+1 i=i+1 bv7=BitVecVal(0x7,32) i=0 while i<3: j=0 while j<3: s.add(Extract(7,0,(((ZeroExt(24,matrix1[i*3])* ZeroExt(24,matrix2[j]))%bv7+ (ZeroExt(24,matrix1[i*3+1])*ZeroExt(24,matrix2[j+3]))%bv7+ (ZeroExt(24,matrix1[i*3+2])*ZeroExt(24,matrix2[j+6]))%bv7)%bv7)) == result[i*3+j]) j=j+1 i=i+1 print s.check() password='' i=0 m=s.model() i=0 while i<18: password=password+chr(m.evaluate(passw[i]).as_long()) i=i+1 print 'Serial: '+password if __name__=="__main__": if len(sys.argv)<2: print "You need to enter your email" else: Find(sys.argv[1])Может показаться, что программа зависла, но это не так. Sbox усложняет работу Z3, и в некоторых местах он скатывается на перебор, но все равно получается на порядки быстрее, чем прямой перебор по восемнадцати символам. Получаем серийник:
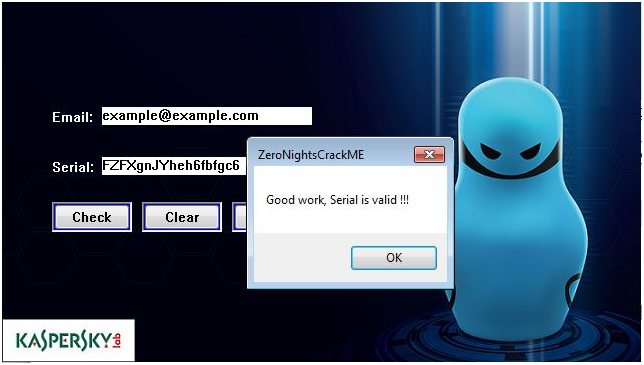
Sat Serial: FZFXgnJYheh6fbfgc6Настало время проверить результаты. Вводим.
Вуаля — ключ подошел. Поиск серийника занял у меня на ноутбуке примерно пятнадцать минут.
Z3 API in Python
Z3 is a high performance theorem prover developed at Microsoft Research. Z3 is used in many applications such as: software/hardware verification and testing, constraint solving, analysis of hybrid systems, security, biology (in silico analysis), and geometrical problems.
This tutorial demonstrates the main capabilities of Z3Py: the Z3 API in Python. No Python background is needed to read this tutorial. However, it is useful to learn Python (a fun language!) at some point, and there are many excellent free resources for doing so (Python Tutorial).
The Z3 distribution also contains the C, .Net and OCaml APIs. The source code of Z3Py is available in the Z3 distribution, feel free to modify it to meet your needs. The source code also demonstrates how to use new features in Z3 4.0. Other cool front-ends for Z3 include Scala^Z3 and SBV.
Be sure to follow along with the examples by clicking the load in editor link in the corner. See what Z3Py says, try your own scripts, and experiment!
Please send feedback, comments and/or corrections to leonardo@microsoft.com. Your comments are very valuable.
Getting Started
Let us start with the following simple example:
x = Int('x') y = Int('y') solve(x > 2, y 10, x + 2*y == 7)