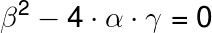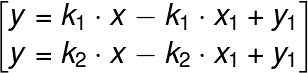блог JOHN_16
Здесь я планирую размещать небольшие статьи на интересующие меня темы.
воскресенье, 18 октября 2015 г.
Python: модуль SymPy. Пример символьных вычислений.
SymPy — это обширный Python модуль реализующий символные вычисления. В качестве примера будет разобрана реальная математическая задача.
Дана окружность радиусом r с координатами центра в точке (x0, y0). Также дана точка с координатами (x1, y1). Необходимо провести лучи из центра окружности, проходящие через точку пересечения окружности и касательных. Все элементы задачи находятся на одной плоскости.
Задача составная, поэтому разделим ее на логически отделенные части, решающие наиболее важные асппекты: 1) нахождение касательных 2)нахождение точек пересечения касательной и окружности. После каждой части будет приведен фрагмент кода, подкрепленный комментариями.
Часть 1. Нахождение касательных
Для начала решим задачу в общем виде. Запишем математическое выражение окружности и касательной в виде системы уравнений:
На два уравнения приходится три неизвестных (x,y,k), с математической точки зрения система имеет множество решений, однако далее мы введем условие, которое разрешит данное положение. Из уравнения прямой выразим y:
И подставим в уравнение окружности, далее, обобщив, получим квадратное уравнение:
По определению касательная и окружность имеют только одну точку пересечения. Это возможно только в случае, если квадратное уравнение имеет 1 корень. По определению квадратного уравнения оно имеет 1 корень в случае, если дискриминант равен нулю:
Решая полученное уравнение получаем несколько значений k1, k2. Подставляем значения в общее уравнение прямой и получаем пару уравнений касательных проведенных из точки (x1, y1) к окружности
Для демонстрации численного решения воспользуемся следующими начальными данными: окружность радиусом 4 с центром в точке (-5, 1) и точка касательной с координатами (10, 15).
# -*- coding: utf-8 -*- from sympy import * import numpy as np # точка центра окружности x0 = -5 y0 = 1 # радиус окружности r = 4 # точка вершины прямой x1 = 10 y1 = 15 # Определяем переменные x, y, k = symbols('x y k') # Выражаем y из уравнения касательной exp_2 = k * (x - x1) - (y - y1) # решаем полученное выражение относительно y # функция solve всегда возвращает список решений, но поскольку мы заранее знаем, что # решений может быть только одно, явно извлекаем нулевой элемент ny = solve(exp_2, y)[0] print 'y=', ny # Выражаем x из уравнений окружности, подставляя ранее полученное # выражение y exp = (x - x0) ** 2 + (ny - y0) ** 2 - r ** 2 # приводим выражение к общему виду относительно переменной x функцией collect, # метод cancel позволяет "упростить" выражение, преобразовав подобные элементы ne = collect(exp.cancel(), x) # преобразуем выражения в объект полинома po = poly_from_expr(ne, x)[0] # выделяем коэфициенты квадратного уравнения alpha = po.coeff_monomial(x**2) beta = po.coeff_monomial(x) gamma = po.coeff_monomial(1) print 'alpha =', alpha print 'beta =', beta print 'gamma =', gamma # Касательная и окружность пересекаются в одной точке, поэтому уравнение # должно иметь только 1 корень, это происходит в случае когда дискриминант # равен нулю. Решаем уравнение и находим значения углового коэффициента D_exp = beta ** 2 - 4 * alpha * gamma res = solve(D_exp, k) # evalf метод вычисляет выражение в численной форме # здесь мы его используем что бы получить более наглядное представление print 'k =', res, '~~>', [_.evalf() for _ in res] # Подставляем полученные значения k и получаем уравнения касательных. tangents_lines = [] for item in res: # метод subs осуществляет подстановку значений в переменные и возвращает # новое выражение tangents_lines.append(ny.subs(k:item>)) print 'y_tangent =', tangents_lines[-1] , '~~>', tangents_lines[-1].evalf()
y= k*x — 10*k + 15
alpha = k**2 + 1
beta = -20*k**2 + 28*k + 10
gamma = 100*k**2 — 280*k + 205
k = [-36*sqrt(5)/209 + 210/209, 36*sqrt(5)/209 + 210/209] ~~> [0.619624654593338, 1.38994472339709]
y_tangent = x*(-36*sqrt(5)/209 + 210/209) + 360*sqrt(5)/209 + 1035/209 ~~> 0.619624654593337*x + 8.80375345406662
y_tangent = x*(36*sqrt(5)/209 + 210/209) — 360*sqrt(5)/209 + 1035/209 ~~> 1.38994472339709*x + 1.10055276602907
Часть 2. Поиск точек пересечений касательных и окружности
Библиотека SymPy для задач аналитической геометрии предоставляет геометрические объекты и различного рода функции для работы с ними. В продолжение прошлой части кода, зададим такие объекты и найдем их точки пересечений, которыми воспользуемся для определения других геометрических объектов.
# список в котором будут храниться точки пересечений intersections = [] # задаем объект окружности circle = Circle(Point(x0, y0), r) # задаем точку из которой будем строить касательную main_point = Point(x1, y1) # для каждой касательной ищем пересечение с окружностью for tangent in tangents_lines: # задаем вторую точку касательной new_point = Point(x0, tangent.subs(x:x0>)) # если вдруг так получилось что точки совпали, то зададим небольшое смещение # и пересчитаем координаты точки if main_point == new_point: new_point = Point(x0 + 1, tangent.subs(x:x0 + 1>)) # задаем объект линию, проходящую через заданные ранее точки line = Line(main_point, new_point) # находим пересечение двух геометрических объектов с помощью # функции intersection, которая вернет список точек пересечений tmp = intersection(circle, line) # если список tmp не пуст, значит пересечения были найдены if tmp: # если длина списка равна единице, то значит все хорошо # для данного случая - мы нашли одну единственну точку пересечения # что соответсвует определению касательной к окружности if len(tmp) == 1: intersections.append(tmp[0]) # если вдруг нашлось более одного пересечения, то в каком то уголке вселенной # нерадивый ученик разделил на ноль, извлек корень из минус единицы # и определил последнее число Пи после запятой. else: print 'I don\'t know how it was, but this is your points: <>'.format(tmp) else: print 'Circle "<>" and line "<>" have no intersection'.format(circle, line) # # # Строим лучи с вершиной в центре окружности, проходящие через точки пересечения с касательной lines = [] for inter in intersections: lines.append(Ray(Point(x0,y0), inter)) print 'Ray', lines[-1], 'pretty views points of ray', [_.evalf() for _ in lines[-1].args]
Вывод данного фрагмента кода будет следующим:
Ray Ray(Point(-5, 1), Point(-1865/421 — 504*sqrt(5)/421, 645/421 + 540*sqrt(5)/421)) pretty views points of ray [Point(-5.00000000000000, 1.00000000000000), Point(-7.10683672365771, 4.40018220391897)]
Ray Ray(Point(-5, 1), Point(-1865/421 + 504*sqrt(5)/421, -540*sqrt(5)/421 + 645/421)) pretty views points of ray [Point(-5.00000000000000, 1.00000000000000), Point(-1.75302075852757, -1.33604918729189)]
Заключение
На рисунке ниже графически представлены некоторые результаты вычислений. Черным цветом нарисованы исходные положения — окружность и точка. Красными оттенками нарисованы две касательные, построенные по вычиленным уравнениям. Зеленым цветом отмечены лучи, исходящие из центра окружности, и, проходящие через точки пересечений касательной и окружности, которые были расчитаны во второй части этого сообщения.
Поставленная задача успешно решена с помощью возможностей предоставляемой библиотекой SymPy.
Basic Operations#
Here we discuss some of the most basic operations needed for expression manipulation in SymPy. Some more advanced operations will be discussed later in the advanced expression manipulation section.
>>> from sympy import * >>> x, y, z = symbols("x y z")
Substitution#
One of the most common things you might want to do with a mathematical expression is substitution. Substitution replaces all instances of something in an expression with something else. It is done using the subs method. For example
>>> expr = cos(x) + 1 >>> expr.subs(x, y) cos(y) + 1
Substitution is usually done for one of two reasons:
- Evaluating an expression at a point. For example, if our expression is cos(x) + 1 and we want to evaluate it at the point x = 0 , so that we get cos(0) + 1 , which is 2.
>>> expr = x**y >>> expr x**y >>> expr = expr.subs(y, x**y) >>> expr x**(x**y) >>> expr = expr.subs(y, x**x) >>> expr x**(x**(x**x))
The second is if we want to perform a very controlled simplification, or perhaps a simplification that SymPy is otherwise unable to do. For example, say we have \(\sin(2x) + \cos(2x)\) , and we want to replace \(\sin(2x)\) with \(2\sin(x)\cos(x)\) . As we will learn later, the function expand_trig does this. However, this function will also expand \(\cos(2x)\) , which we may not want. While there are ways to perform such precise simplification, and we will learn some of them in the advanced expression manipulation section, an easy way is to just replace \(\sin(2x)\) with \(2\sin(x)\cos(x)\) .
>>> expr = sin(2*x) + cos(2*x) >>> expand_trig(expr) 2*sin(x)*cos(x) + 2*cos(x)**2 - 1 >>> expr.subs(sin(2*x), 2*sin(x)*cos(x)) 2*sin(x)*cos(x) + cos(2*x)
There are two important things to note about subs . First, it returns a new expression. SymPy objects are immutable. That means that subs does not modify it in-place. For example
>>> expr = cos(x) >>> expr.subs(x, 0) 1 >>> expr cos(x) >>> x x
SymPy expressions are immutable. No function will change them in-place.
Here, we see that performing expr.subs(x, 0) leaves expr unchanged. In fact, since SymPy expressions are immutable, no function will change them in-place. All functions will return new expressions.
To perform multiple substitutions at once, pass a list of (old, new) pairs to subs .
>>> expr = x**3 + 4*x*y - z >>> expr.subs([(x, 2), (y, 4), (z, 0)]) 40
It is often useful to combine this with a list comprehension to do a large set of similar replacements all at once. For example, say we had \(x^4 — 4x^3 + 4x^2 — 2x + 3\) and we wanted to replace all instances of \(x\) that have an even power with \(y\) , to get \(y^4 — 4x^3 + 4y^2 — 2x + 3\) .
>>> expr = x**4 - 4*x**3 + 4*x**2 - 2*x + 3 >>> replacements = [(x**i, y**i) for i in range(5) if i % 2 == 0] >>> expr.subs(replacements) -4*x**3 - 2*x + y**4 + 4*y**2 + 3
Converting Strings to SymPy Expressions#
The sympify function (that’s sympify , not to be confused with simplify ) can be used to convert strings into SymPy expressions.
>>> str_expr = "x**2 + 3*x - 1/2" >>> expr = sympify(str_expr) >>> expr x**2 + 3*x - 1/2 >>> expr.subs(x, 2) 19/2
sympify uses eval . Don’t use it on unsanitized input.
evalf #
To evaluate a numerical expression into a floating point number, use evalf .
>>> expr = sqrt(8) >>> expr.evalf() 2.82842712474619
SymPy can evaluate floating point expressions to arbitrary precision. By default, 15 digits of precision are used, but you can pass any number as the argument to evalf . Let’s compute the first 100 digits of \(\pi\) .
>>> pi.evalf(100) 3.141592653589793238462643383279502884197169399375105820974944592307816406286208998628034825342117068
To numerically evaluate an expression with a Symbol at a point, we might use subs followed by evalf , but it is more efficient and numerically stable to pass the substitution to evalf using the subs flag, which takes a dictionary of Symbol: point pairs.
>>> expr = cos(2*x) >>> expr.evalf(subs=x: 2.4>) 0.0874989834394464
Sometimes there are roundoff errors smaller than the desired precision that remain after an expression is evaluated. Such numbers can be removed at the user’s discretion by setting the chop flag to True.
>>> one = cos(1)**2 + sin(1)**2 >>> (one - 1).evalf() -0.e-124 >>> (one - 1).evalf(chop=True) 0
lambdify #
subs and evalf are good if you want to do simple evaluation, but if you intend to evaluate an expression at many points, there are more efficient ways. For example, if you wanted to evaluate an expression at a thousand points, using SymPy would be far slower than it needs to be, especially if you only care about machine precision. Instead, you should use libraries like NumPy and SciPy.
The easiest way to convert a SymPy expression to an expression that can be numerically evaluated is to use the lambdify function. lambdify acts like a lambda function, except it converts the SymPy names to the names of the given numerical library, usually NumPy. For example
>>> import numpy >>> a = numpy.arange(10) >>> expr = sin(x) >>> f = lambdify(x, expr, "numpy") >>> f(a) [ 0. 0.84147098 0.90929743 0.14112001 -0.7568025 -0.95892427 -0.2794155 0.6569866 0.98935825 0.41211849]
lambdify uses eval . Don’t use it on unsanitized input.
You can use other libraries than NumPy. For example, to use the standard library math module, use «math» .
>>> f = lambdify(x, expr, "math") >>> f(0.1) 0.0998334166468
To use lambdify with numerical libraries that it does not know about, pass a dictionary of sympy_name:numerical_function pairs. For example
>>> def mysin(x): . """ . My sine. Note that this is only accurate for small x. . """ . return x >>> f = lambdify(x, expr, "sin":mysin>) >>> f(0.1) 0.1