Создание генератора простых чисел
Доброго времени суток, начал изучать Python. Нужно написать программу для генерации простых чисел.
Ругается на:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33
import math; import random; import time; def eznum(): timez=time.time(0) timez+=10 random.random(timez) while 1: z=0 i=2 a=random.randint(1,100) for i in range(i,a,1) if a%i==1 continue if a%i==0 z=1 break if z==0 break return a; def main(): p = eznum() print(p) if __name__ == '__main__': main()
Создание генератора пароля
И так задача состоит в создании генератора пароля с указанием от пользователя количества символов в.
Создание генератора слов
Прошу вас помочь создать генератор определенных слов, допустим есть около 3000 слов, которые.
Написание генератора простых чисел
Составить программу-генератор простых чисел , в основу положить формулу 2х2+29 при 0≤ х ≤28
Помогите переписать с паскаля на C#. Проверка генератора простых чисел
задача "Утверждается, что функция f=n2+n+41 является генератором простых чисел при n не равных 41.
Сообщение от Mindfure
тебя не смутило что ты i используешь и как стартовое значение и как элемент из итератора? в алфавите 26 букв, выбери плиз другую)
Стоп, а отступ передан for зачем?
Добавлено через 26 секунд
i = 2 и сразу вертишь его в цикле, опять i
Добавлено через 18 секунд
Welemir1, Ёлки — палки чего вы такие быстрые все?!
Сообщение от Mindfure
from random import randint a = randint(1, 100) i = 2 for i in range(i, a, 1): print(i)
Damenikx, погоди, то что i два раза использовано еще не ошибка, просто так делать не нужно, надо узнать что ему интерпретатор пишет
Может быть так ты хотел, но всё равно, опять i и снова i
Добавлено через 27 секунд
Welemir1, я ему написал с его любимой буквой, может быть так и надо
Во-первых отступ 14 строка он там не нужен. Во-вторых после for нет двоеточия.
Добавлено через 2 минуты
После всех if поставить двоеточие. Ретурн сместить вправо на один таб.
Добавлено через 1 минуту
Сообщение от Mindfure
Мать моя женщина Уберите точки с запятой это же Python. Какое у тебя задание вообще?) Сейчас мы подскажем, как это написать. Если же ты только начал, зачем тебе функции? Почитай начальную документацию, про отступы и обозначения.
Mindfure, оратор выше забыл добавить что ты вообще что-то странное там делаешь, рандомы какието, время. ты точно понимаешь как искать простые числа и что такое генератор?
В Python’e действия происходят построчно (почти все, функции и т.д., можно вызывать в любой части кода). Тебе нужен генератор просто чисел. Хочешь научиться — необязательно сразу лезть в функции. Дедушка Лутц даёт функции а в середине книги, 440 страница (вроде как).
Добавлено через 46 секунд
Welemir1, оратор Я ещё не кончил, закончил!
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
def eznum(): timez=time.time(0) timez+=10 random.random(timez) while 1: z=0 a=random.randint(1,100) for i in range(2,a,1): if a%i==1: continue if a%i==0: z=1 break if z==0: break return a;
if __name__ == '__main__': main()
Вот ты знаешь зачем это? Я вот тоже не знаю пока что, поэтому не использую, но мне кажется ты пришёл с c# либо что-то похожее, где необходимо писать всё в функции вызова (либо в классе, либо в методе). Тебе для запуска программы этого не надо!
Mindfure, убери точку с запятой после ретурна, и поставь его правее на один таб.
Добавлено через 1 минуту
Твои if делают проверки, которые согласно твоему коду не сбудутся НИКОГДА! Ведь ты рандом начинаешь с цифры 2, как он может быть 0 или 1 — никак.
Mindfure, а как ты изучаешь пайтон, просто пишешь по аналогии? просто с отступами все плохо, надо бы литературы почитать, у нас тут своя атмосфера
Добавлено через 1 минуту
from math import sqrt from itertools import count, islice def isPrime(n): if n 2: return False for number in islice(count(2), int(sqrt(n)-1)): if not n%number: return print(0) return print(1) isPrime(10)
создание генератора случайных чисел
необходимо создать реально случайные числа, которые не будут зависеть от каких либо факторов (я.
Создание генератора случайных чисел (little frog generator)
Создала первую часть задания, но вот с остальными проблемы, не получается даже вывести элементы с.
Создание генератора рандомных чисел с возможностью задания диапазона
Windows Forms Visual c++ Я Хотел бы сделать Генератор Рандомный Чисел С Возможностью Задать.
Создание файлов с данными, полученными с помощью генератора случайных чисел
помогите пожалуйста!заранее благодарна На C#. Выполнить задания с использованием текстового.
Нахождение простых, взаимно-простых и парно-простых чисел из указанного диапазона
Нужна помощь мне нужно создать программу для нахождение простых,взаимнопростых и парно простых.
Загадки Python — Генерация простых чисел!
Обычно существует несколько способов решения задач даже пограничной сложности. Как же определить оптимальное и эффективное решение?
В этой статье мы представим достаточно простую задачу с несколькими решениями, чтобы показать, как думать и оценивать оптимизацию вычислительной сложности. Оптимизацию памяти мы обсудим в другой статье, возможно, на другом примере.
ПОСТАНОВКА ЗАДАЧИ
Давайте обратимся к одной из фундаментальных проблем математики: определение и генерация набора простых чисел меньше заданного целого числа. Ваша задача — создать эффективный метод (как алгоритмически, так и программно) для оптимизации вычислительных ресурсов.
Математическое определение:
Простое число определяется как любое положительное целое число больше 1, которое не делится ни на какое целое число, кроме 1 и самого себя.
Входной аргумент:
N = 35 (используется в качестве примера)
Ожидаемый результат:
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31]
Ограничения:
Нет. Однако обсудите различные методы оптимизации.
РЕШЕНИЕ
Мы начнем с самого простого подхода и будем совершенствовать его для оптимизации решения алгоритмически и программно.
Простейшее решение
Верные приведенному выше определению, мы начинаем с числа 2 и анализируем каждое целое число до N и смотрим, делится ли оно на любое целое число, кроме 1 и самого себя. Если да, то переходим к следующему целому числу. В противном случае мы собираем его как простое число и переходим к следующему числу.
def get_primes(N):
primes = []
for n in range(2,N):
for d in range(2,n):
if n%d==0:
break
else:
primes.append(n)
return primes
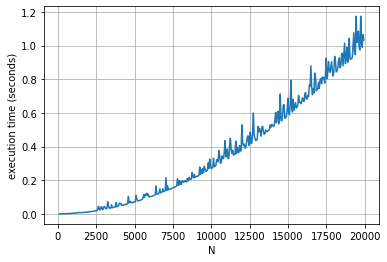
Очевидно, что приведенный выше код выдает все простые числа ниже N, однако он является довольно простым, проверяя каждое число, что примерно приводит к вычислительной сложности порядка O(N²), как показано на диаграмме ниже. Если N невелико, алгоритм не занимает много времени, но по мере роста N время вычисления всех простых чисел ниже N растет нелинейно. Поэтому большие значения N будут занимать все больше времени.
Информацию о некоторых подходах к бенчмаркингу Python можно найти в этой статье.
Алгоритмическая оптимизация
Объединив то, что мы знаем о простых числах математически, и то, что Python может делать программно, мы можем добиться некоторого снижения вычислительной сложности. Хотя этот анализ относится к генерации простых чисел, аналогичный процесс может быть использован для оптимизации любой вычислительной реализации.
Теперь давайте рассмотрим некоторые алгоритмические факты, которые мы знаем при генерации простых чисел. Возможно, некоторые из них вы помните из школьного курса математики.
- Любое четное число больше 2 не может быть простым числом (мы можем объединить этот факт с пропуском счета чисел в Python).
- При нахождении коэффициентов (делители, дающие 0 в качестве остатка) нам нужно проверять делители только до sqrt(N) из-за симметрии факторизации (можно остановиться внутри цикла, когда мы достигнем sqrt(N)).
- Наконец, при проверке делимости нам нужно рассматривать простые числа только как факторы. Объединив это с №2, мы должны рассматривать простые числа до sqrt(N) как потенциальные делители для проверки делимости.
Существуют и другие алгоритмические оптимизации для генерации простых чисел, но эта статья больше посвящена изучению реализации Python, чем простым числам.
Приведенный ниже код реализует эти алгоритмические оптимизации, причем строки четко обозначают, какая техника оптимизации алгоритма реализуется.
def get_primes_opt(N):
primes = []
for n in range(3,N,2): #optimization-1
is_prime = True
for d in primes: #optimization-3
if d*d > n: #оптимизация-2
break
if n%d==0:
is_prime = False
break
if is_prime:
primes.append(n)
return [2] + primes
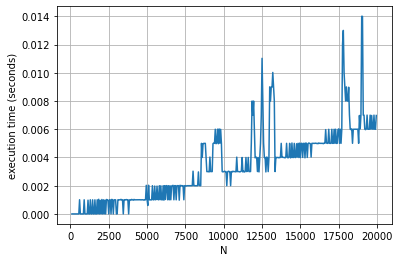
Давайте посмотрим, как это отразится на вычислительных ресурсах. Ниже приведен график, на котором показано время выполнения для различных значений N.
Как вы можете видеть, это занимает значительно меньше времени. Не каждое выполнение точно такое же, некоторые прогоны занимают немного больше времени из-за конкурирующего использования ресурсов. В целом, однако, оптимизированный алгоритм работает намного быстрее, чем первоначальная рудиментарная реализация. Эта оптимизация приводит к вычислительной сложности порядка O(log(N)).
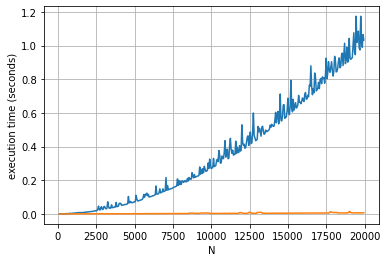
Было бы весьма эффектно увидеть их бок о бок, как показано ниже.
Оказывается, что оптимизированное решение примерно в 100 раз быстрее (для максимального значения N, использованного для тестирования), чем рудиментарное неоптимизированное решение. Это может иметь огромное значение для больших значений N.
Программная оптимизация
Конечно, математика приходит на помощь! Но можем ли мы сделать ее более эффективной, переписав нашу функцию по-другому? Да, если ваша задача заключается в многократном вычислении простых чисел при заданном N для многих различных значений N.
Скажем, раньше мы использовали 1000 для N, а теперь нам нужны простые числа до 1200, действительно ли нам нужно снова генерировать все простые числа до 1000? Нет, если вы их где-то храните.
Мы можем переписать нашу реализацию как класс, и хранить уже вычисленные простые числа как переменную класса, а повторно генерировать только при необходимости. Реализация для этого показана ниже.
class PrimeNumbers:
def __init__(self):
self.__last_processed_N = 2
self.__next_start = 3
self.__primes = [2]
def __generate_primes__(self, N):
if N return #нет необходимости генерировать снова для меньших Ns
for n in range(self.__next_start,N,2):
is_prime = True
for d in self.__primes:
if d*d > n:
break
if n%d==0:
is_prime = False
break
if is_prime:
self.__primes.append(n)
self.__last_processed_N = N
self.__next_start = N if N%2 else N+1
def get_primes(self, N):
self.__generate_primes__(N)
retval = []
for x in self.__primes:
if x >= N:
break
retval.append(x)
return retval
p = PrimeNumbers(
)p1000 = p.get_primes(1000)
p1200 = p.get_primes(1200)
# последняя строка запускает генерацию простых чисел только для чисел между #1000
и 1200, повторно используя ранее вычисленные простые числа.
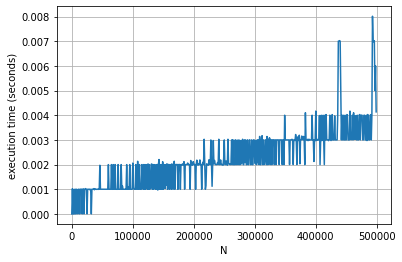
В качестве примера для измерения производительности давайте вычислим простые числа для значений N от 100 до 500000 с шагом 1000.
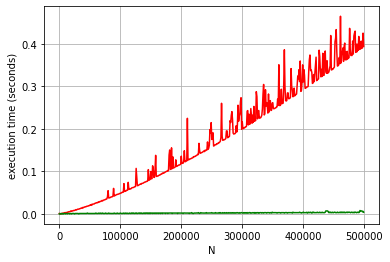
Как вы можете видеть, время значительно сократилось. Давайте посмотрим, как это сопоставимо с оптимизацией только алгоритма (который заново генерирует простые числа каждый раз, когда мы вызываем функцию). Ниже показано боковое сравнение алгоритмической оптимизации и решения Class для инкрементного вычисления в партиях по 1000 чисел.
Как видно из графика, инкрементное вычисление может быть довольно эффективным в определенных сценариях. Например, когда N равно 500000 (последний цикл), оптимизированный алгоритм занял 400 мс, в то время как реализация Incremental Class заняла менее 10 мс (так как рассматривала только последние 1000 чисел в качестве кандидатов) и искала все простые числа ниже 499000 из памяти.
ЗАКЛЮЧЕНИЕ
При внедрении и разработке программ всегда (ВСЕГДА) помните об эффективности. Не нужно тратить лишние вычислительные ресурсы даже для простых реализаций.
Следите за новыми головоломками Python и не забудьте оставить мне сообщение!