- Set Operations in Python
- The difference_update Method
- The symmetric_difference Method
- Union of Sets
- Intersection of Sets
- Subtract Two Sets in Python
- 1. Quick Examples of Subtraction operation on Sets
- 3. Set subtraction using – operator
- 3.1 Set ‘-‘ operator Syntax
- 3.2 Examples
- 4. Set subtraction using difference_update()
- 4.1 Set difference_update() Syntax
- 4.2 Examples
- 5. Conclusion
- Related Articles
- You may also like reading:
- Операции над множествами, сравнение множеств
- Объединение множеств
- Вычитание множеств
- Симметричная разность
- Сравнение множеств
Set Operations in Python
In some of my previous articles we were talking about the basics of sets and set methods . If you’re interested, feel free to read them. Today we’ll be talking about set operations. There are several set operations we can use: difference, union, intersection and some more. They are pretty much like the operations on sets in mathematics.
You can also watch the video version of this article:
Comprehensive, for Kivy beginners, easy to follow.
Get the book here (PDF) or on Amazon:
There is an even shorter syntax to find the difference of two sets. We can just use the minus operator:
We can find the difference of more than two sets:
>>> numbers = >>> odd_numbers = >>> prime_numbers =
Let’s find all the numbers that are in numbers but not in odd_numbers. So we get .
Then let’s find those of the above numbers which are not in prime_numbers. So we get only even composite (= not prime) numbers:
>>> even_composite_numbers = numbers.difference(odd_numbers).difference(prime_numbers) >>> even_composite_numbers
We can also use the shortcut here:
>>> numbers - odd_numbers - prime_numbers
Make Awesome Games and Other 3D Apps
with Panda3D and Blender using Python.
Cool stuff, easy to follow articles.
Get the magazine here (PDF) .
The difference_update Method
A similar method is difference_update. It works like difference plus it removes all the elements of another set from the set it’s called on:
>>> elements = >>> nonmetals = >>> elements.difference_update(nonmetals) >>> elements
Here we have a shortcut as well. Instead of using the method x.difference_update(y)we can use the minus operator x = x – y.
>>> elements = >>> nonmetals = >>> elements = elements - nonmetals >>> elements
or even shorter, the -= augmented operator:
>>> elements = >>> nonmetals = >>> elements -= nonmetals >>> elements
Learn the basics of Python, including OOP.
with lots of exercises, easy to follow
The course is available on Udemy .
The symmetric_difference Method
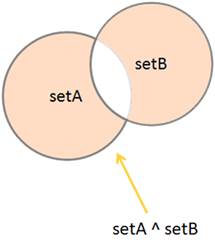
Another method is symmetric_difference. It returns a new set with the elements in either of the two sets but not in both:
>>> prime_numbers = >>> numbers_above_10 = >>> prime_numbers.symmetric_difference(numbers_above_10)
The shortcut for this method is ^, So x ^ y works like x.symmetric_difference(y):
>>> prime_numbers ^ numbers_above_10
Union of Sets
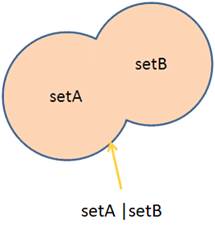
The method union is used to return a union of two sets as a new set. The union contains all elements that are in either set:
>>> big_mammals = >>> african_mammals = >>> mammals = big_mammals.union(african_mammals) >>> mammals
A shortcut for this method also exists. It’s the pipe operator |. So x | y works like x.union(y):
>>> big_mammals | african_mammals
Learn the basics of 3D modeling in Blender.
step-by-step, easy to follow, visually rich
The course is available on Udemy and on Skillshare .
Intersection of Sets
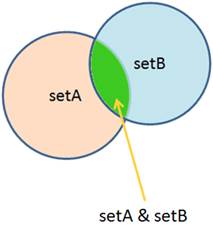
Another method is intersection. It returns the intersection of two sets as a new set. The intersection contains all elements that belong to both of the sets:
>>> odd_numbers = >>> prime_numbers = >>> odd_prime_numbers = odd_numbers.intersection(prime_numbers) >>> odd_prime_numbers
This method has a shortcut as well. It’s the ampersand operator &. So x & y works like x.intersection(y):
>>> odd_numbers & prime_numbers
Subtract Two Sets in Python
To subtract two sets in Python use the difference() method. This method is called on one set and takes the second set as a parameter. Alternatively, you can also use – operator.
1. Quick Examples of Subtraction operation on Sets
Following are quick examples of how to perform Subtraction operations on sets.
2. Set Subtraction using difference() method
The difference() method is used to get elements from the first set such that all these elements are not present in any of the sets.
2.1 Set difference() Syntax
Let’s see the syntax for difference().
2.2 Examples of difference() method
Example 1: Let’s create two sets and perform subtraction operation for both using difference() method.
print("Set 1: ",myset1) myset2 = print("Set 2: ",myset2) # Set2 - Set1 print("Set2 - Set1: ",myset2.difference(myset1)) # Set1 - Set2 print("Set1 - Set2: ",myset1.difference(myset2)) # Output: # Set 1: # Set 2: # Set2 - Set1: # Set1 - Set2: - ‘sparkby’ is only element present in set2 but not in set1.
- 56 and 43 are the elements present in set1 but not in set2.
Example 2: Let’s create four sets and perform subtraction operations using difference() method.
- 56 and 43 are the elements present in set1 but not in set2.
- 56, 43, 12, ‘Hello’ are the elements present in set1 but not in set4.
- 89, 67 are the elements present in set4 but not in set3.
- All elements are same in set1 and set3, So empty set is returned.
Example 3: Let’s create four sets and perform subtraction operations using difference() method.
myset2 = myset3 = myset4 = # Set1 - Set2 - Set3 print("Set1 - Set2 - Set3: ",myset1.difference(myset2,myset3)) # Set4 - Set2 - Set3 print("Set4 - Set2 - Set3: ",myset4.difference(myset2,myset3)) # Output: # Set1 - Set2 - Set3: set() # Set4 - Set2 - Set3: - We are performing subtraction on first set with second and third sets, Empty set is returned.
- 89, 67 are the elements present in set4 but not in set2 and set3.
3. Set subtraction using – operator
‘-‘ is similar to difference() method. The difference is that we will use ‘-‘ (Minus) operator instead of method.
3.1 Set ‘-‘ operator Syntax
Let’s see the syntax for ‘-‘ Minus operator.
3.2 Examples
Example 1: Let’s create two sets and perform subtraction operation for both using difference() method.
print("Set 1: ",myset1) myset2 = print("Set 2: ",myset2) # Set2 - Set1 print("Set2 - Set1: ",myset2-myset1) # Set1 - Set2 print("Set1 - Set2: ",myset1-myset2) # Output: # Set 1: # Set 2: # Set2 - Set1: # Set1 - Set2: print("Set 1: ",myset1) myset2 = print("Set 2: ",myset2) myset3 = print("Set 3: ",myset3) # Set1 - Set2 - Set3 print("Set1 - Set2 - Set3: ",myset1-myset2-myset3) # Set1 - Set2 print("Set1 - Set2: ",myset1-myset2) # Output: # Set 1: # Set 2: # Set 3: # Set1 - Set2 - Set3: set() # Set1 - Set2: 4. Set subtraction using difference_update()
difference_update() is similar to difference(), But the difference is that difference() will return new set and difference_update() will store the result in the first set.
4.1 Set difference_update() Syntax
Let’s see the syntax for difference_update() method
4.2 Examples
Example 1: Let’s create two sets and subtract first set from the second set.
print("Set 1: ",myset1) myset2 = print("Set 2: ",myset2) # Set2 - Set1 myset2.difference_update(myset1) print("Set 2: ",myset2) # Output: # Set 1: # Set 2: # Set 2: You can see that ‘sparkby’ is only one that exists in set2 but not in set1. And also the result is stored in myset2.
Let’s create two sets and subtract second set from the first set.
print("Set 1: ",myset1) myset2 = print("Set 2: ",myset2) # Set1 - Set2 myset1.difference_update(myset2) print("Set 1: ",myset1) # Output: # Set 1: # Set 2: # Set 1: You can see that 43 and 56 exists in set1 but not in set2. And also they are stored in myset1.
5. Conclusion
In this article, we have seen how to perform set subtraction in Python using difference(),’-‘ operator and difference_update() method with examples. difference() method will return new set but the difference_update() will store the result in the first set.’-‘ operator is similar to the difference() method.
Related Articles
You may also like reading:
Операции над множествами, сравнение множеств
На выходе получаем новое множество, состоящее из значений, общих для множеств setA и setB. Это и есть операция пересечения двух множеств. При этом, исходные множества остаются без изменений. Здесь именно создается новое множество с результатом выполнения этой операции. Разумеется, чтобы в дальнейшем в программе работать с полученным результатом, его нужно сохранить через какую-либо переменную, например, так:
То есть, мы вычисляем результат пересечения и сохраняем его в переменной seta и, как бы, меняем само множество setA. А вот если взять множество:
будет пустое множество. Обычно, на практике используют оператор пересечения &, но вместо него можно использовать специальный метод:
setA = {1, 2, 3, 4} setB = {3, 4, 5, 6, 7} setA.intersection(setB)
Результат будет тем же, на выходе получим третье множество, состоящее из общих значений множеств setA и setB. Если же мы хотим выполнить аналог операции:
setA.intersection_update(setB)
В результате, меняется само множество setA, в котором хранятся значения пересечения двух множеств. Вот такие способы вычислений пересечения множеств существуют в Python.
Объединение множеств
setA = {1, 2, 3, 4} setB = {3, 4, 5, 6, 7} setA | setB
На выходе также получаем новое множество, состоящее из всех значений обоих множеств, разумеется, без их дублирования. Или же можно воспользоваться эквивалентным методом:
который возвращает множество из объединенных значений. При этом, сами множества остаются без изменений. Операцию объединения можно записать также в виде:
Тогда уже само множество setA будет хранить результат объединения двух множеств, то есть, оно изменится. Множество setB останется без изменений.
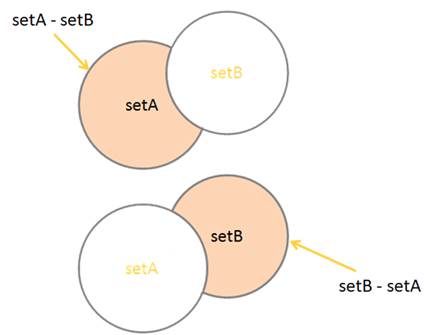
Вычитание множеств
возвратит новое множество, в котором из множества setA будут удалены все значения, повторяющиеся в множестве setB: <1, 2> Или, наоборот, если из множества setB вычесть множество setA:
то получим значения из которых исключены величины, входящие в множество setA. Также здесь можно выполнять эквивалентные операции:
Симметричная разность
Наконец, последняя операции над множествами – симметричная разность, возвращает множество, состоящее из неповторяющихся значений обоих множеств. Реализуется она следующим образом:
setA = {1,2,3,4} setB = {3,4,5,6,7} setA ^ setB
На выходе получим третье, новое множество, состоящее из значений, не входящих одновременно в оба множества.
Сравнение множеств
В заключение этого занятия я хочу показать вам, как можно сравнивать множества между собой. Предположим, имеются два таких множества:
setA = {7, 6, 5, 4, 3} setB = {3, 4, 5, 6, 7}
И мы хотим узнать, равны они или нет. Для этого, используется уже знакомый нам оператор сравнения на равенство:
Увидим значение True (истина). Почему? Дело в том, что множества считаются равными, если все элементы, входящие в одно из них, также принадлежат другому и мощности этих множеств равны (то есть они содержат одинаковое число элементов). Наши множества setA и setB удовлетворяют этим условиям. Соответственно, противоположное сравнение на не равенство, выполняется, следующим образом:
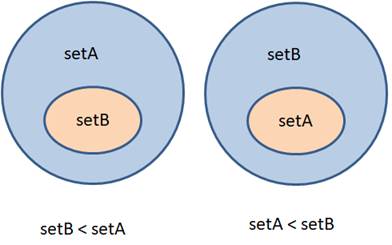
Следующие два оператора сравнения на больше и меньше, фактически, определяют, входит ли одно множество в другое или нет. Например, возьмем множества
setA = {7, 6, 5, 4, 3} setB = {3, 4, 5}