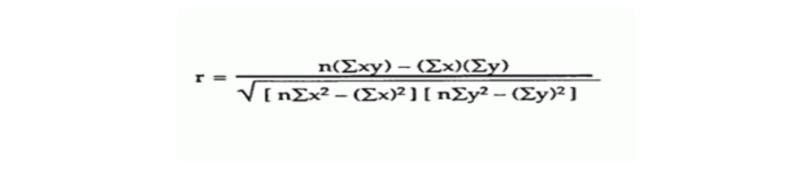Python seaborn correlation matrix

Introduction to the Correlation Matrix

The correlation matrix is a matrix that shows the correlation between variables. It gives the correlation between all the possible pairs of values in a matrix format.

Sanskar Wagavkar is a data analyst studying for his master’s in data science from Pune University. He has previously worked as a data analyst for Verificient Technologies. Wagavkar specializes in data visualization, machine learning and statistics.

The correlation matrix is a matrix that shows the correlation between variables. It gives the correlation between all the possible pairs of values in a matrix format. We can use a correlation matrix to summarize a large data set and to identify patterns and make a decision according to it. We can also see which variable is more correlated to which variable, and we can visualize our results. A correlation matrix involves a rows and columns table that shows the variables. Every cell in a matrix contains the correlation coefficient. The correlation matrix is in conjunction with other types of statistical analysis. It’s very useful for regression techniques like simple linear regression , multiple linear regression and lasso regression models. In the regression technique, we have several independent variables, and based on that, we are predicting the dependent variable.

What Is a Correlation Matrix?

A correlation matrix is a statistical technique used to evaluate the relationship between two variables in a data set. The matrix is a table in which every cell contains a correlation coefficient, where 1 is considered a strong relationship between variables, 0 a neutral relationship and -1 a not strong relationship. It’s most commonly used in building regression models.

In multiple linear regression, the correlation matrix determines the correlation coefficients between the independent variables of a model.

When Do You Use the Correlation Matrix?

• If the relationship is 1, then the relationship is strong.
• If the relationship is 0, then it means the relationship is neutral.
• If the relationship is -1, then it means the relationship is negative or not strong.
• By using a correlation matrix, you can better understand your data set, analyze it and visualize the result.
• Most data scientists consider this the main step before building any machine learning model because if you know which variables are correlated which, you can gain a better understanding about what’s most important for your model.
• The correlation matrix is a statistical technique that gives you the values between -1 to 1 which you can determine the relationship between variables.

Finding the Correlation Coefficient in a Correlation Matrix

Correlation Coefficient

Before building a correlation matrix, you need to understand what a correlation coefficient is and its different types.

Correlation coefficients are used to determine how strong a relationship is between two variables. There are several types of correlation coefficients.

Types of Correlation coefficients:

1. Sample correlation coefficients.
2. Population correlation coefficients.
3. Pearson correlation coefficients.

How to Calculate Correlation Coefficient

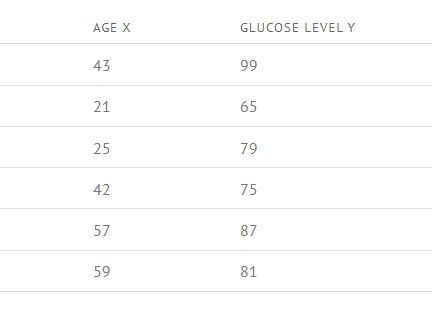
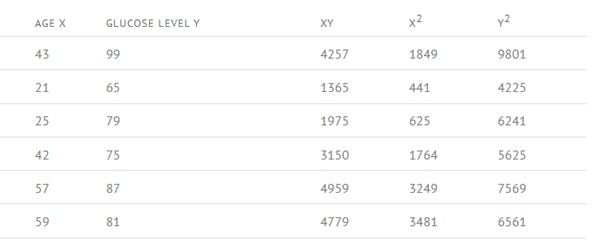
For example, let’s find the correlation coefficient of the given table

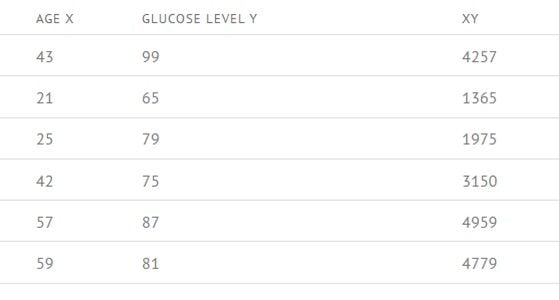
Step 1 : Calculate AGE X * GLUCOSE LEVEL Y for each value in the table.

Step 2: Now calculate X2 and Y2 for each value in the table.

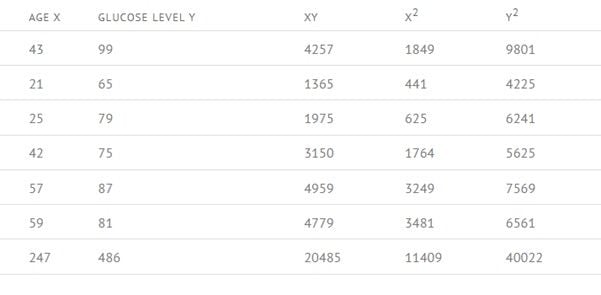
Step 3: Now calculate the sigma (Σ) for every column.

Step 4: Now we are going to use the Pearson correlation coefficient formula.

Values are: n = 6 , Σxy = 20485 , Σx = 247 , Σy = 486 , Σ = 11409 , Σ = 40022 , r = 0.5298 ……(from formula).

By putting values inside this formula, we can calculate how strong the relationship is between two variables. So, by entering those values, we get 0.5298, which means our relationship is greater than neutral and less than positive

That’s how we can calculate the correlation coefficient of each value and make a matrix from it.

Correlation Matrix Implementation in Python

We can easily implement a correlation matrix in Python because Python has a large library of support, and for statistical analysis, we can use Pandas and NumPy .

Most data analysts implement their correlation matrix in Python because Python has a powerful package that helps us to do data pre-pressing, and we can make great visualizations .

There are some certain steps you need to follow to implement the correlation matrix:

Step 1: Collect the Data From Various Sources

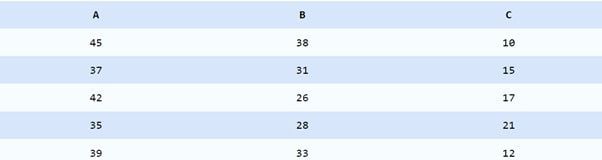
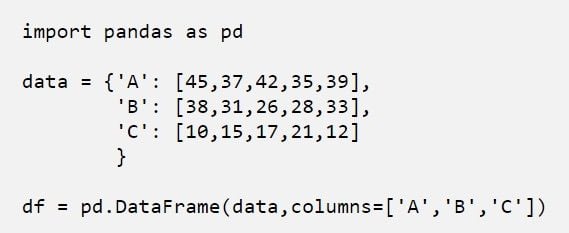
Collect the data from various sources for the correlation matrix. The following data is about three variables.

Step 2: Create a DataFrame of A, B, C Using Pandas

We’ve now created a DataFrame using Pandas. Now, we have three variables, A, B and C.

Step 3: Create a Correlation Matrix Using the “Corr” Function

Output:

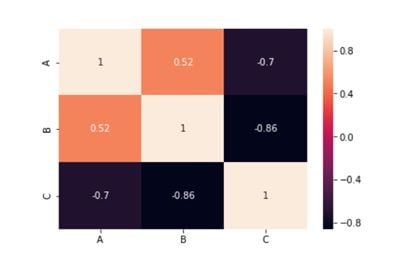
By using the corr function we have created a correlation matrix that looks like the above image.

Step 3: Visual Representation of Correlation Matrix Using Matplotlib and Seaborn

Output:

That’s how you can implement a correlation matrix in Python, through which we can get a better understanding about which variables are highly correlated to each other.

Correlation Matrix Applications

• We can summarize a large amount of data in which the goal is to identify patterns. In our example above, the observable pattern is that all the variables highly correlate with each other.
• To input into other analyses. For example, people commonly use the correlation matrix as inputs for exploratory factor analysis, confirmatory factor analysis, structural equation models, and linear regression when excluding missing values pairwise.
• As a diagnostic when checking other analyses For example, with linear regression, a high number of correlations suggests that the linear regression estimates will be unreliable.

We can use the correlation matrix in the machine learning model to improve accuracy, and we can create a confusion matrix to understand the data.

We can use this statistical technique in the health care sector as well to predict diseases.

Correlation Matrix Advantages

The correlation matrix is a very useful statistical technique by which we can gain a better understanding of our data set and get a summary of it. That way we can analyze the data and make a decision according to it. If you are building any machine learning model, this technique can help you select which data and features will be most impactful. The correlation matrix is the most popular statistical technique, so it has large support and it can easily be implemented in Python or any other programming language .

Источник

Plot Correlation Matrix and Heatmaps between columns using Pandas and Seaborn.

The correlation measures dependence between two variables. It also measures “how two variables move together” and “how strongly they have related” means the increase in one variable also an increase in another.It helps you get a deeper understanding of your data.

For example, sales might increase in the festival season, or a customer’s purchase on an e-commerce website might depend on a number of factors.

DataSet

For illustration, I’ll use the Auto-mpg dataset, containing Mileage per gallon performances of various cars.

import numpy as np import pandas as pd auto_df=pd.read_csv('auto-mpg.csv')

Correlation Coefficient between two Columns

Correlation expressed in the form of a correlation coefficient. For example, the following data shows the number of Cylinders and the Displacement of cars.

Using the correlation coefficient you can find out how these two variables are related and to what degree. Please note that this is only a part of the whole dataset.

To calculate the correlation coefficient, selecting columns, and then applying the .corr() method. We can compute the correlation pairwise between more than 2 columns.

auto_df[['cylinders','displacement']].corr()

 cylinders displacement cylinders 1.000000 0.950721 displacement 0.950721 1.000000

In this way, we found the correlation coefficient between ‘Cylinders’ and ‘Displacement’ is 0.95. This value will change according to the size of the dataset.

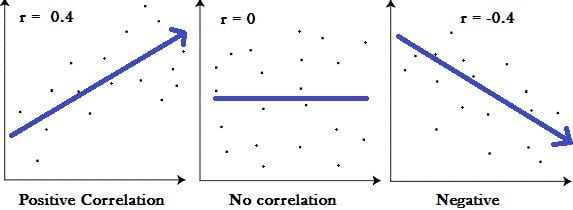
Positive Correlation Coefficient

The correlation coefficient is measured on a scale from -1 to +1. A positive correlation coefficient means that there is a perfect positive relationship between the two variables.

Here Both features move together in the same direction. An increase in one is accompanied by an increase in the other.

Negative Correlation Coefficient

A correlation coefficient of (-) represents a perfect negative correlation. This means when one increases, the other decreases and vice-versa.

Zero Correlation

A value of 0, means that there is no correlation between the two and they are not related to each other at all.

In our example, we got a positive number for the correlation coefficient, which confirms that an increase in salary is in fact related to an increase in job satisfaction.

Correlation Matrix

Making a correlation matrix is a great way to summarize all the data. In this way, you can pick the best features and use them for further processing your data.

Pandas’ DataFrame class has the method corr() that computes three different correlation coefficients. Using any of the following methods: Pearson correlation, Kendall Tau correlation, and Spearman correlation method. The correlation coefficients calculated using these methods vary from +1 to -1.

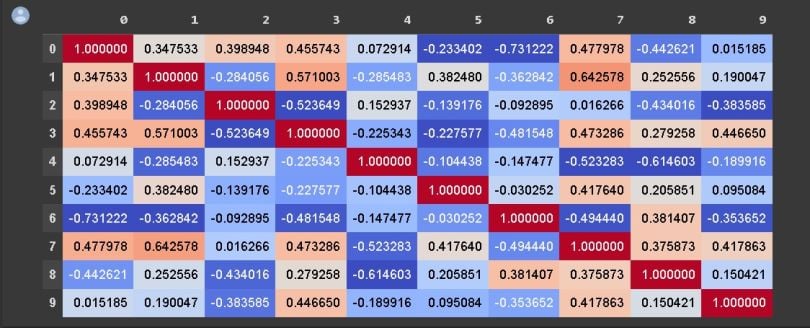
Below is a correlation matrix to find out which factors have the most effect on MPG. All the variables involved have been placed along with both the column header and the row header of the table. Correlation coefficients between each pair of variables have been calculated and placed at their intersections.

This matrix tells a lot about the relationships between the variables involved. You will find a correlation of 1.0 along the diagonal of the matrix. This is because each variable is highly and positively correlated with itself. You can also see the relationship between “mpg” and “weight” is -0.8. This means as Car weight increase, chances of car mpg decreases.

A good way to quickly check correlations among columns is by visualizing the correlation matrix as a heatmap.

Heatmaps

Visualization is generally easier to understand than reading tabular data, heatmaps are typically used to visualize correlation matrices. A simple way to plot a heatmap in Python is by importing and implementing the Seaborn library.

import seaborn as sns sns.heatmap(auto_df.corr(), annot = True, fmt='.2g',cmap= 'coolwarm')

Dark red means positive, Blue means negative. The stronger the color, the larger the correlation magnitude.

Remove Correlated Features

Correlated features, in general, don’t improve models but they affect specific models in different ways and to varying extents. It is clear that correlated features means that they bring the same information, so it is logical to remove one of them.

corrMatrix=auto_df.corr().abs() upperMatrix = corr_matrix.where(np.triu(np.ones(corrMatrix.shape), k=1).astype(np.bool)) # Find index of feature columns with correlation greater than 0.90 corrFutures = [column for column in upperMatrix.columns if any(upperMatrix[column] > 0.90)] auto_df.drop(columns=corrFutures)

Run this code in Google Colab

Related Post

Источник